DP，入门？？？

初始动态规划　　

　　想要回答"什么是动态规划"这种问题从来是很困难的,动态规划有着广阔的内涵,
　　我们或许可以这样概括:
　　求解一类最优化问题,将原问题划分成子问题,子问题有非常工整的结构.

　　DP术语:状态,状态转移方程.
　　子问题图:以状态为点,以状态之间的转移为边.
　　子问题图是一个DAG.

　　DP的顺序:
　　　　递推 (bottom-up method)
　　　　记忆化搜索 (top-down with memoziation)
　　问题的内涵:最值,方案,方案数.

一般思路

　　一般dp形式为前i个元素，通过考虑最后一个元素的选择来转移

最大子段和

　　luoguP1115

　　给出一段序列，选出其中连续且非空的一段使得这段和最大。　　

　　解法一: 考虑最短负前缀, 要么是最大子段和是其前缀, 要么与最大子段和无交.
　　解法二: DP, f_i 表示以 i 为结尾的最大子段和 (可能为空),f_i = max(f_i-1, 0) + a_i.
　　解法三: 考虑前缀和, 问题变成求max_0≤i<j≤n{s_j - s_i} = max_1≤j≤n{s_j - min_0≤i<j{si}}　　

//dp思路
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;

int n;
long long ans=-23333,a[200002],b[200002];

int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i)
	{
		scanf("%lld",&a[i]);
		b[i]=max(a[i]+b[i-1],a[i]);
		ans=max(b[i],ans);
	}	
	printf("%lld",ans);
	return 0;
}

动态最大子段和　　

　　维护一个序列, 支持单点修改和查询区间最大子段和
　　n,m ≤3*10^5

　　使用线段树, 每个区间维护:

　　　　包含左端点的最大子段和

　　　　包含右端点的最大子段和

　　　　最大子段和

　　　　区间和

最长上升子序列　　　

　　  一个长度为 s 的上升子序列 P 被定义为
　　P = (i₁,……, i_s), 1 < i₁ <……< i_s, a_i1 < a_i2 <……< a_is,
　　求最长的上升子序列的长度是多少?
　　n ≤10^6　　

　　解法一: f(i) 表示以 i 结尾的最长上升子序列.

　　

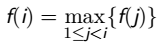
　　使用树状数组求前缀 max　　

　　解法二: 按 j 从小到大的顺序求 f(j), 对于每一个 k, 使用一个数组 g 维护 min{ai}, f(i) = k　　

　　在 g 中套一个 vector, vector 每个元素记录历史权值大小和方案数的前缀和.

最长公共子序列　　

　　已知两个整数序列 {a_n}, {b_n}, 求它们的最长公共子序列.
　　长度为 s 的公共子序列定义为
　　(i₁, i₂, · · · , i_s), i₁ < i₂ < · · · < i_s,

　　a_i1 = b_i1,a_i2 = b_i2, · · · , a_in = b_in
　　n ≤ 5000　　

　　f(i, j) 表示 a_1--i, b_1--j 的最长公共子序列.

　　

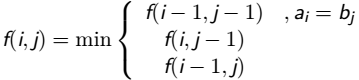
最优矩阵链乘　　　

　　有 n 个矩阵 A1, A2,……, An, 每个矩阵的大小是 pi × qi, 求计算∏ⁿ_i=1 Ai 最少需要多少次整数乘法? 有多少种方案来计算这个乘积?
　　n ≤ 5000
　　f(l,r) 表示把 [l,r] 的矩阵乘起来的最少需要的整数乘法次数.

　 

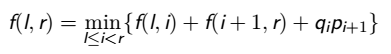
　　方案数: Catlan 数

区间DP（一般思路）　　

　　状态为区间.
　　常见的有两种转移方法:
　　　　考虑区间端点处的选择.
　　　　考虑区间的划分.
　　后者复杂度可能较高, 可以通过四边形不等式优化.

环形DP（一般形式）　　

　　一般处理环有两种方法:
　　　　将环倍长, 将环的条件改对区间长度的限制条件
　　　　枚举环中的一点, 破环为链

 树形DP（一般形式）　　

　　往往在 LCA 处统计信息: 链, 连通点集, 子树...
　　LCA 的性质:
　　　　LCA(a, b) = LCA(b, a)
　　　　LCA(LCA(a, b), c) = LCA(a, LCA(b, c)
　　所以我们可以定义 LCA(A), A ⊆ V.

 

状压DP（一般思路）　　

　　DP 状态是一个集合 S.
　　常见转移:
　　　　枚举某一个元素选/不选.
　　　　枚举子集