图论
引
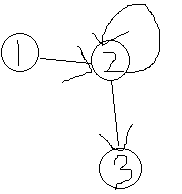
经典的七桥问题:
问怎样走能经过所有的桥并且每个桥只经过一次;

开始并不知道第二个图是怎么到的第三个图,然后某zz是这么说的;

所以就是这样了;
然后又是经典的国际象棋问题:
国际象棋棋盘为8*8期盼,但我们一般是要扩展到n*m的,然后就要知道,马在棋盘上是怎么走的呢?
Δx=1,Δy=2或者Δx=2,Δy=1;当然可能我们一般理解或者做题的时候,是在格点上操作的,
但应该要转化到格子上去理解和操作,如图:
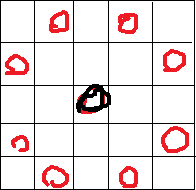
然后要说的就是,nm取值的影响了,首先nm都是奇数,则无法构成回路(不能回到原来的位置);
当n==1时,则无法完成移动步数为2的情况,所以无解;
当n==2时,
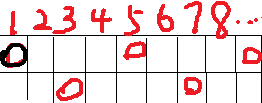
很明显所能到达的点的列数必定与初始所在列数奇偶性相同;
当n==4时,我们引入黑白染色,红蓝染色这个说法,
规定如下棋盘:

很明显途中有四个类型的格子:红黑,红白,蓝黑,蓝白;
那么它一次能到达的所有可能的格子中,没有一个会是与原来这个格子染色情况相同的,
如图:
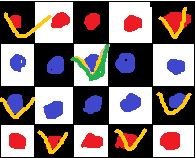
这时我们可以把整个棋盘分成两半,
一半的染色情况是:红+黑 和 蓝+白,另一半的染色情况是:红+白 和 蓝+黑;
但我们可以发现这与上图是矛盾的,我们每次走一步的两种情况的可能性并不是1:1,
所以不能遍历到整个图;
……更大的情况略;
一些图的基本概念
节 (结, 顶) 点 (node): 图的基本构成元素, 一般以小写字母表示 (u, v, ...).
标号: 大部分图论算法是建立在有标号节点之上的.
边 (edge): 节点对 (u,v). 可分为有向边 (有序节点对) 和无向边 (无序节点对),
对于有向边, u 称作始点, v 称作终点.
重边: 相同的边
自环: (u,u)
图 (graph): G = (V,E). 其中 V 是点集, E 是可重边集.
各种图:
无向图, 有向图, 混合图.
简单图 (无重边和自环)
完全图 (K n ), 竞赛图
DAG:有向无环图;
补充:完全图:边最多的简单图,可以理解为,任意一对节点之间都有边,像这样
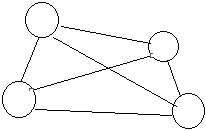
那么竞赛图呢?:就是一个完全图,但是每个边都赋有一个方向,像这样:
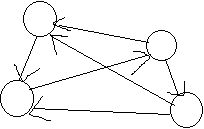
权
边权: w : E → R/N
点权: w : V → R/N
度
度:边与点的相遇;
度: d : V → N, 与某节点相邻的边数.
正 (出) 度: 以某节点为始点的边数.
负 (入) 度: 以某节点为终点的边数.
有根树和无根树度的定义不同,(一个包含所有入度出度,,另一个,,,)
度的性质:

度为奇数的节点必为偶数个.(只对竞赛图)
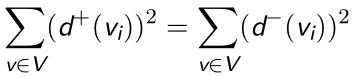
图的存储

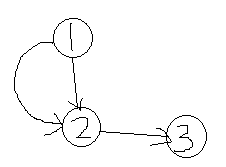
例如上图
邻接矩阵:a[i][j],(无向图a[j][i]) ,缺点:不能记重边;
前向星: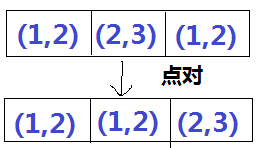
十字链表,如图:

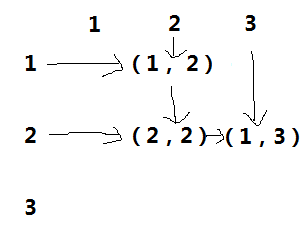
查询指定边信息?
邻接矩阵: O(1)
前向星: O(E)/O(logE)
邻接表/十字链表: O(E)/O(logE)
路径
有向路径: P = (e 1 ,...,e n ), 其中 e i 的终点是 e i+1 的始点.
初等: 路径经过的边两两不同.
简单: 路径经过的点两两不同 (除路径的始点与终点外).
环: 路径的始点与终点相同.
无向图上的路径: 存在一种每一条边分配方向的方案使得其成为一条有向图的路径.
自由树
自由树: 连通的无环无向图.
森林: 树的集合.
对于一棵自由树而言, 以下 6 条等价:
1.G 是一棵自由树.
2.G 中任何两顶点由唯一简单路径相连.
3.G 是连通的, 但是从图中移除任意一条边得到的图均不连通.(都是桥)
4.G 是连通的, 且 |E| = |V| - 1
5.G 是无环的, 且 |E| = |V| - 1
6.G 是无环的, 但若向 E 中添加任意一条边, 均会造成该图包含恰有一个环.
有根树与二叉树
有根树: 自由树 + 根.
节点之间的关系: 父亲与儿子, (真) 祖先与 (真) 后代, 叶节点.
子树: u 的所有后代的导出子图.
定义在点集上的函数: 度, 深度, 大小.
导出子图是什么?
设V1是V的一个非空子集,以V1为顶点集,
以两端点均在V1中的边的全体为边集的子图称为G的导出子图.
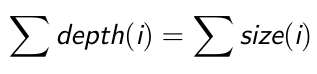
二叉树:左子树,右子树
一些性质:
任何非空二叉树中,度为2的节点数比叶节点数少1.
n个节点的二叉树高度至少为 logn(下取整)
Kraft 不等式: 将二叉树 T 中每个深度为 d 的叶节点赋予权值 w(x) = 2-d,则∑w(x) ≤1.
树的存储
可以保存的信息:
边信息
父亲
儿子
大部分题会将树作为一个无向图来读入, 也有的题会告诉你某个点的父亲是谁, 保存哪些信息取决于你的需求.
图的遍历
BFS(breadth first search): 求图中两点间最短路径?
(路径长度被定义为其拥有的边数)
时间复杂度: O(V + E)
BFS 生成树
DFS(depth first search): DFS 生成树.
边的分类:
树边
后向边(指向祖先的边)
前向边(指向后代的边)
横向边(既不指向祖先,也不指向后代的边)
性质:
括号化定理 ([vl,vr])
无向图 G 不存在横向边
联通
连通: 若图G的任意两点间均存在路径,则称图G连通.
子图: 若G'= (V',E') 满足 V'⊆V, E'⊆E, 则称 G'是G的子图.
导出子图:若E'包含了G在 V'中的所有边,则称 G'是G关于 V 的导出子图.
(无向图的) 极大连通子图 (连通支): 若 G'满足不存在 H,
使得 G'是 H 的子图, H 是 G 的子图, 则称 G'是 G 的极大连通子图.
拓扑排序
在DAG(Directed Acyclic Graph,有向无环图)中求一个排列P,
使得对于每个点v而言,若(u,v)存在,则u在P中在v之前.
Kahn算法:不断寻找入度为0的点.
基于DFS的算法:以vr排序.
欧拉路径: 经过所有边的简单路径.
欧拉回路: 经过所有边的简单环.
欧拉路径(环)
连通无向图:
存在欧拉回路 等价于度为奇数的点有 0 个.
存在欧拉路径 等价于度为奇数的点有 0 或 2 个.
连通有向图 (边忽略方向后得到的无向图连通):
存在欧拉回路 等价于所有点出入度相等.
存在欧拉路径 等价于所有点出入度相等 或恰有一个点
入度比出度多 1 和恰有 1 个点出度比入度多 1.
如何求出一条欧拉路径?
Prop.若G中有k个度为奇数的点,G可以划分为k/2条简单道路.
最短路
最短路:有向边权图中两点间的所有路径中最短的一条.(若不连通,定义为 ∞)
负权边:负权图的最短路径中可能有无穷多条边.
环路:不可能包含回路 ;
松弛操作: d(x,v) = min(d(x,v),d(x,u)+w(u,v))
三角不等式: d(x,v) ≤d(x,u)+w(u,v)
最短路径树与最短路径图
Dijkstra
算法流程:维护已经找到最短路的点集S,不断地寻找距离S最近的点将其加入S.
仅适用于边权非负的图.
时间复杂度:O((V+E)log(V+E))/O((V+E)logV)/O(VlogV+E)
Bellman-Ford
for(int i=n;i;--i)
for(int j=m;j;--j)
dis[v[j]]=min(dis[v[j]],dis[u[j]]+w[j]);
不断在最短路中加边.
时间复杂度: O(VE)
SPFA: deprecated
Hack: 网格图, 次短路条数很多的图.
Floyd
for(int k=n; k; --k)
for(int i=n; i; --i)
for(int j=n; j; --j)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
可以看作 DP.
同时求出每对点间的最短路.
时间复杂度: O(V^3)
Johnson
每对顶点间的最短距离(稀疏有向图)
重新赋予权重: w'(u,v)=w(u,v)+d(0,u)-d(0,v)
一遍 Bellman-Ford+|V|遍Dijkstra.
时间复杂度: O(V2logV + VE)
应用: 差分约束系统

若 x = (x1,……,xn) 是差分约束系统的一个解,
则 x + d 也是差分约束系统的一个解.
约束图: 新建 0 点, w(0, i)(1 ≤i ≤n) 为 0; w(jl, il) 为 kl.
强连通分量
强连通分量 (SCC, Strongly Connected Component):
有向图的极大点集 C ⊆ V, C 中任意两点可达.
Kosaraju 算法: 以 vr 逆序对 GT = (V, ET) 作 DFS,则每棵DFS 树会是一个 SCC.
Tarjan 算法: 使用一个栈来维护尚未被分到 SCC 中的节点,
依据一个节点 u 是否能走到其 DFS 树中的祖先 (low(u)),来取出栈中节点分配成一个新的 SCC.
Gabow 算法: 使用两个栈来取代 low, S 表示尚未被分配的节点, P 表示尚未被分配 SCC 的节点.
时间复杂度均为 O(V + E)
将 SCC 缩点, 原图变为 DAG.
边双连通分量
桥 (割边): 删掉之后会导致图不连通的边.
边双连通分量 (BCC, biconnected component) 的等价定义:
极大连通导出子图,不含桥.
极大连通导出子图,使得任意两点间均有两条边不相交路径.
极大连通导出子图,使得任意两条边都存在于一个简单回路中.
极大连通导出子图,任意三点 a, b, c, 存在边不相交的路径 a → b, b →c.
极大连通导出子图,存在一种给边赋向的方案使得其为SCC.
判断割边: low(u) = ul
将 BCC 缩点, 原图变为树.
点双连通分量
割点: 删掉之后会导致图不连通的点.
点双连通分量 (块, block) 的等价定义:
极大连通导出子图,删除其中任意一个点不会使其不连通.
极大连通导出子图,任意两个点之间有两条点不相交路径.
极大连通导出子图,任意三点 a, b, c 之间, 两条点不相交路径.
注意到两个块可以有至多一个交点.
割点的等价条件:
根节点是割点当且仅当其DFS树至少有两个子树.
非根节点是割点当且仅当 low(u) < ul.
将 Block 缩成环, 原图变为仙人掌.
最小生成树基本概念:环与割
切割: (S, V -- S), 对 V 的一个划分.
横跨: (u, v) 一个端点在 S, 另一个端点在 V -- S, 则称 (u, v)横跨割 (S, V -- S).
尊重: 边集 A 中不存在横跨割 (S, V - S) 的边, 则称(S, V -- S) 尊重 A.
轻量级边: (u, v) 是横跨 (S, V -- S) 的所有边中权重最小的.
MST 基本定理
对于任意 A ⊆ E, 存在 G 的最小生成树 T, A ⊆ T, 任意e = (u, v) ∈ A,
存在尊重 A 的切割 (S, V -- S), (u, v) 是(S, V -- S) 的一条轻量级边,
令 B = A ∪ (u, v), 则存在最小生成树 T', B ⊆ T'.(这条边被称作安全边)
MST 的求解算法
Prim 算法: 类似于 BFS/Dijkstra, 维护一个连通的 A, 不断寻找 (A, S -- A) 中的轻量级边.
时间复杂度: O((V + E)logV) / O(VlogV + E)
Kruskal 算法: 从小到大枚举每条边 (u, v), 若 u 和 v 在 A 中尚不连通, 就将 (u, v) 加入 A.
时间复杂度: O(V + E log E)
Boruvka 算法: 找到每个点的最小邻边, 形成了环套树森林,将每一个环套树缩点.
时间复杂度: O((V + E)logV)
MST 的性质
若图 G 的一条边 (u, v) 在某棵最小生成树 T 中,则该条边是某个切割 (S, V -- S) 的轻量级边.
任意两棵最小生成树的有序边权序列相同.
对于非负边权图, MST 等价于权值和最小的边集, 使得图连通.
MST 是瓶颈生成树 (最大边权最小的生成树).
最近公共祖先:LCA问题
LCA(Lowest Common Ancestor, 最近公共祖先):
LCA(u,v) 定义为 u 和 v 的所有公共祖先中深度最大的那一个.
倍增: fa[u][j] 表示从 u 向上跳 2^j 步可以到达的点.
时间复杂度: O(n log n) -- O(log n)
树链剖分: 重儿子是所有儿子中 size 最大的那个.
时间复杂度: O(n) -- O(log n)
DFS 序 +ST: 利用 DFS 序的性质将问题转化为求区间最小值, 再使用 Sparse Table 求解.
时间复杂度: O(n log n) -- O(1)
Tarjan: 离线查询, 使用并查集维护当前栈中节点已经遍历过的子树.
时间复杂度: O(n + m)
与 RMQ 问题的联系
RMQ(Range Minimum/Maximum Query): 查询区间最值.
静态: ST(Sparse Table)(O(n log n) -- O(1)).
动态: 线段树 (O(n) -- O(log n)).
从 LCA 到 RMQ: 利用 DFS 序.(特殊的 ±1 RMQ)
从 RMQ 到 LCA: 利用笛卡尔树.
在线查询的线性做法: 以 log n/2 为大小分块, 再使用 Sparse Table.
时间复杂度: O(n) -- O(1)

