图论学习七之Cut & Bridge
需要解决的问题
• 无向图的割点、割点集合与点连通度
• 无向图的桥、 割边集合与边连通度
• 无向图的割点与点双连通分量的求法
• 无向图的桥与边双连通分量的求法、边双连通分量的构造
• 相关例题讨论
割点
• 在无向连通图G上进行如下定义:
• 割点:若删掉某点P后, G分裂为两个或两个以上的子图,则称P
为G的割点。
• 割点集合: 在无向连通图G中,如果有一个顶点集合,删除这个
顶点集合以及与该点集中的顶点相关联的边以后, 原图分成多于
一个连通块,则称这个点集为G的割点集合。
• 点连通度:最小割点集合的大小称为无向图G的点连通度。
割边
• 类似地,在无向连通图G上进行如下定义:
• 桥(割边):若删掉某条边b后, G分裂为两个或两个以上的子图,
则称B为G的桥(割边)。
• 割边集合:如果有一个边集合,删除这个边集以后, 原图分成多
于一个连通块, 则称这个边集为割边集合。
• 边连通度:最小割边集合的大小称为无向图G的边连通度。
双连通分量
• 点双连通图:点连通度大于1的图称为点双连通图(没有割点)。
• 边双连通图:边连通度大于1的图称为边双连通图(没有割边)。
• 无向图G=<V,E>的极大(点/边)双连通子图称为(点/边)双连通分量。
• 缩点:把一个双连通分量G’=G[V’]=<V’,E’>缩为一个点的过程,就
是删除该双连通分量内的所有点(V’)和所有边(E’),然后新建一个
点,向所有与双连通分量中的点有边相连的外部点(V-V’)连边。
无向图上的经典Tarjan算法
• Tarjan基于对图的深度优先搜索,并对每个节点引入两个值:
• dfn[u]:节点u的时间戳。 记录点u是DFS过程中第几个访问的节点。
• low[u]:节点u或u的子树经过一条回边能够到达的时间戳最小的
节点。
• 对于每一条与u相连的边(u,v):
• 若在搜索树上v是u的子节点,则更新low[u]= min(low[u], low[v]);
• 若(u,v)不是搜索树上的边,则更新low[u]= min(low[u], dfn[v]);
求桥和割点的Tarjan算法
思路和有向图求强连通分量类似
在深度优先遍历整个图过程中形成的一棵搜索树
• 一个顶点u是割点,当且仅当满足(1)或(2)
• (1) u为树根,且u有多于一个子树。
(2) u不为树根,且满足存在(u,v)为树枝边(或称父子边,
即u为v在搜索树中的父亲),使得dfn(u)<=low(v)。
• 一条无向边(u,v)是桥,当且仅当(u,v)为树枝边,且满足
dfn(u)<low(v)(注意重边的情形) 。

• low[u]定义为u或者u的子树中能够通过非父子边追溯到的最
早的节点的DFS开始时间
• 重要的判断:
• if((v,u)和上一步走的边不是同一条)
• 如果去掉这个判断,会发生什么? 就求不出桥了。
• 如果这个判断改成 if(v不是u 的父节点) 则会把重边错当作桥。
在无向图没有重边时,能得出正确的结果
Tarjan’s algorithm
• 也可以先用Tajan()进行dfs算出所有点的low和dfn值,并记录dfs过
程中每个点的父节点,然后再把所有点看一遍,看其low和dfn,以
找出割点和桥。
• 找桥的时候,要注意有没有重边。有重边,则不是桥。
求点双连通分量
• 可以在求割点的过程中维护一个栈求出每个点双连通分量。
• 建立一个栈, 存储DFS过程中访问的节点,初次访问一个点时把
该点入栈。
• 割点可能属于多个点双连通分量, 其余点和每条边属于且仅属于
一个点双连通分量。因此在从栈中取出节点时,要把u留在栈中。
实现
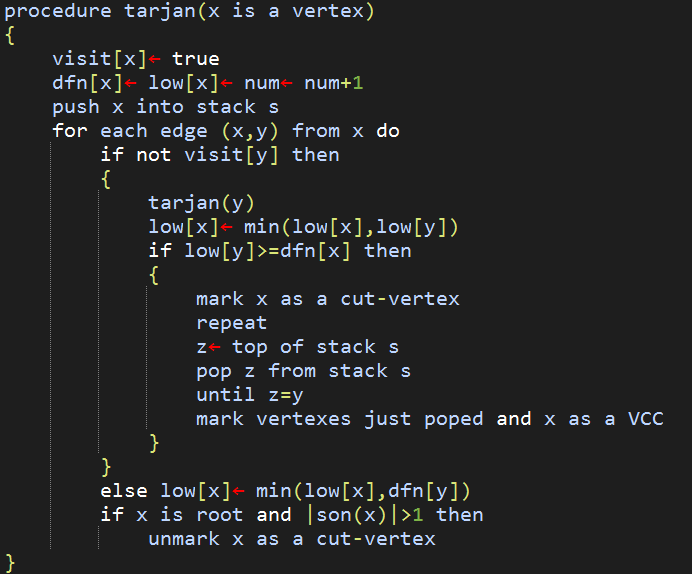
无重边连通无向图求割点和桥的程序
给出点数和所有的边,求割点和桥

求无向图连通图点双连通分支
(不包含割点的极大连通子图):
• 对于点双连通分支,实际上在求割点的过程中就能顺便把每个点
双连通分支求出。建立一个栈,存储当前双连通分支,在搜索图
时,每找到一条树枝边或反向边,就把这条边加入栈中。如果遇
到某时满足dfn(u)<=low(v),说明u是一个割点,同时把边从栈顶
一个个取出,直到遇到了边(u,v),取出的这些边与其关联的点,
组成一个点双连通分支。割点可以属于多个点双连通分支,其余
点和每条边只属于且属于一个点双连通分支。
求无向连通图点双连通分量(没有割点的连通分量) ,假定没有重边

求无向连通图边双连通分支
(不包含桥的极大连通子图)
• 只需在求出所有的桥以后,把桥边删除,原图变成了多个连通块,
则每个连通块就是一个边双连通分支。桥不属于任何一个边双连
通分支,其余的边和每个顶点都属于且只属于一个边双连通分支。
EXAMPLE
POJ-3352 Road Construction
• 给你一个图,要求你加入最少的边,使得最后得到的图为一个边
双连通分支。所谓的边双连通分支,即不存在桥的连通分支。
• 可以求出所有的桥,把桥删掉。然后把所有的连通分支求出来,
显然这些连通分支就是原图中的双连通分支。把它们缩成点,然
后添上刚才删去的桥,就构成了一棵树。在树上添边使得树变成
一个双连通分支即可。
• 本题只要求输出一共需要添加多少条边,而不需要求具体的方案。
其实可以统计度为1的叶子节点(设共有x个),然后直接输出
(x+1)/2即可
命题:一棵有n(n>=2)个叶子结点的树,至少须添加ceil(n/2)
条边,就能转变为一个没有桥的图。或者说,使得图中每
条边,都至少在一个环上。
证明:
这里只证明n为偶数的情况。 n为奇数的证明类似。
先证明添加n/2条边一定可以达成目标。
n=2时,显然只需将这两个叶子间连一条边即可。命题成立。
设n=2k(k>=1)时命题成立,即S[2k]=k。下面将推出n=2(k+1)时命
题亦成立。
n=2k+2时,选取树中最长的迹,设其端点为a,b;并设离a最近的
度>=3的点为a',同理设b'。
(关于a‘和b’的存在性问题:由于a和b的度都为1,因此树中其它
的树枝必然从迹<a,b>之间的某些点引出。否则整棵树就是迹
<a,b>, n=2<2k+2,不可能。)
在a,b间添一条边,则迹<a,b>上的所有边都已不再是桥。
这时,将刚才添加的边,以及aa‘之间, bb’之间的边都删
去,得到一棵新的树。因为删去的那些边都已经符合条件
了,所以在之后的构造中不需要考虑它们。由于之前a‘和b’
的度>=3,所以删除操作不会使他们变成叶子。因此新的
树必然比原树少了两个叶子a,b,共有2k个叶子。由归纳知
需要再加k条边。因此对n=2k+2的树,一共要添加k+1条边。
(最长的迹保证a’,b’不相同)
因此证得n/2可取。
再证明n/2是最小的解。
显然,只有一个叶子结点被新加的边覆盖到,才有可能使
与它相接的那条边进入一个环中。而一次加边至多覆盖2
个叶子。因此n个叶子至少要加n/2条边。
证毕。
求桥
• 对于一条搜索树上的边(u,v),其中u是v的父节点, 若
low[v]>dfn[u], 则(u,v)是桥。
• low[v]表示v和v的子树不经过搜索树上的边能够到达的时间戳最
小的节点;
• low[v]>dfn[u]说明从以v为根的子树到子树之外必须要经过边(u,v),
因此(u,v)是桥。
• 可以像求割点一样,当v回溯至u后,判断上述不等式是否成立。
• 另一种判断方法:当递归v结束时,如果low[v]==dfn[v]说明v和v
的父节点之间的边是桥。
• P.S. 在有重边的图上求桥,需要注意对这些重边加以区分。
求边双连通分量
• 边双连通分量的求法非常简单,
只需在求出所有的桥以后,把
桥边删除。
• 此时原图分成了若干个连通块,
每个连通块就是一个边双连通
分量。
• 桥不属于任何一个边双连通分
量;
• 其余的边和每个顶点都属于且
仅属于一个边双连通分量。
实现
procedure tarjan(x is a vertex)
{
visit[x]←true
dfn[x]←low[x]←num←num+1
for each edge (x,y) from x do
if not visit[y] then
{
tarjan(y)
low[x]←min(low[x],low[y])
if low[y]>dfn[x] then
mark edge (x,y) as a bridge
}
else if edge(y,x) not on DFS tree then
low[x]←min(low[x],dfn[y])
//the following step can also find bridges
if dfn[x]=low[x] then
mark edge into x on DFS tree as a bridge
}
边双连通分量的构造
• 任意给定一个无向连通图,最少添加多少条边可以把它变为边双
连通图?
• 求出所有的桥和边双连通分量,把每个双连通分量缩为一个点。
• 此时的图只包含缩点后的双连通分量和桥边,是一棵无根树。
• 统计树中度数为1的节点的个数cnt。把树变为边双连通图,至少
需要添加(cnt+1)/2条边。
• 构造方法:每次寻找最近公共祖先最远的两个度数为1的节点,
在两点之间连一条边。
• 这样可以使这两个点到LCA的路径上的所有点形成环,环一定是
双连通的。
CF #111 (Div. 2) problem D Edge in MST
• 给出带权连通图G。
• 问哪些边一定出现在MST上,哪些边可以出现在MST上,哪些又
一定不在MST上。
• (MST=最小生成树)
• n, m<=100000
• 考虑一个弱化情形:
• 图G中所有边权都为1
• 自环必定不在生成树上。
• 对于边权相同的边来说,任何顺序都可行
• 我们可以指定任意一条边最先加入
• 因此,剩下的边都可能在生成树上
• 桥必定在生成树上。
• 求最小生成树,按边权从小到大排序依次加边。
• 边权相同的分在同一组,一起处理。
• 每次加完一组后,把每个连通块都分别缩成一个点。
• 按照弱化情形的处理方式处理即可
最近公共祖先
• 离线处理:读入所有的询问(可使用邻接表存储)。
• 给每个节点添加一个颜色标记,尚未访问的标记为0,进入递归
而未回溯的节点标记为1,已经访问过的标记为2。
• 维护一个并查集,访问完某个节点时, 就合并该节点所在的集合
与其父节点所在的集合。
• 正在处理点u时, u和u的所有祖先的标记均为1,已经访问过的节
点均与父节点相连;因此遍历子树u后,考虑所有与u相关的询问
lca(u,v),那么lca(u,v)就是v所在并查集的根。
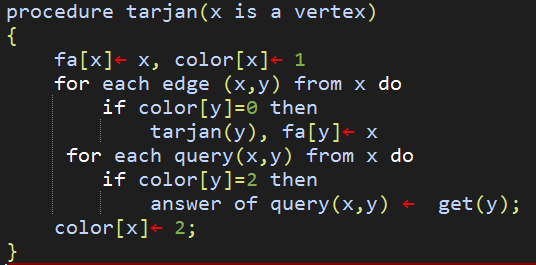
经典Tarjan算法求LCA
如果你不开心,那我就把右边 这个帅傻子分享给你吧,
这个帅傻子分享给你吧,
你看,他这么好看,跟个zz一样看着你,你还伤心吗?
真的!这照片盯上他五秒钟就想笑了。
一切都会过去的。
时间时间会给你答案2333

