图论学习六之Strongly connected components强连通分量
强连通分量(Strongly connected cmponents)
• 在有向图G中,如果任意两个不同的顶点相互可达,则称该有向
图是强连通的。有向图G的极大强连通子图称为G的强连通分支。
• 转置图: 将有向图G中的每一条边反向形成的图称为G的转置GT。
• 原图G和GT的强连通分支是一样的。
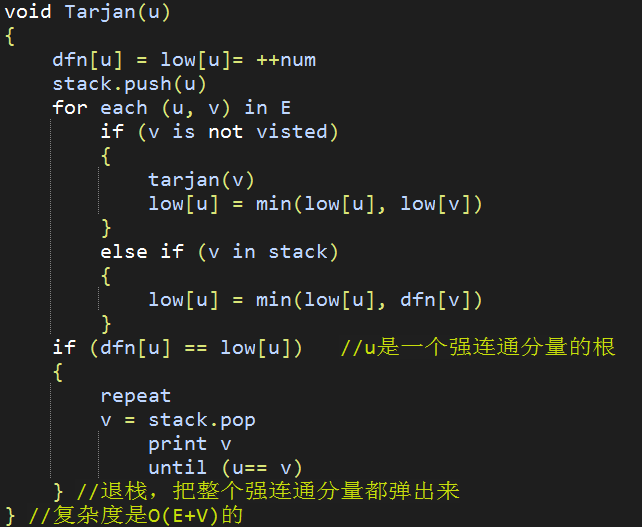
有向图强连通分支的Tarjan算法
• 做一遍DFS,用dfn[i]表示编号为i的节点在DFS过程中的访问序号(也可以叫做
开始时间)用low[i]表示i节点DFS过程中i的下方节点所能到达的开始时间最
早的节点的开始时间。
• 初始时dfn[i]=low[i]
• 在DFS过程中会形成一搜索树。在搜索树上越先遍历到的节点,显然dfn的值
就越小。
• DFS过程中,碰到哪个节点,就将哪个节点入栈。栈中节点只有在其所属的
强连通分量已经全部求出时,才会出栈。
• 如果发现某节点u有边连到搜索树中栈里的节点v,则更新u的low 值为
dfn[v](更新为low[v]也可以)。
有向图强连通分支的Tarjan算法
◦如果一个节点u已经DFS访问结束,而且
此时其low值等于dfn值,则说明u可达的
所有节点,都不能到达任何在u之前被
DFS访问的节点 ---- 那么该节点u就是一
个强连通分量在DFS搜索树中的根。
◦此时将栈中所有节点弹出,包括u,就找
到了一个强连通分量
EXAMPLE
lPOJ2186:Popular Cows
• 给定一个有向图,求有多少个顶点是由任何顶点出发都可达的。
• N<=10000, M<=50000
• 有向无环图中唯一出度为0的点,一定可以由任何点出发均可达
• (由于无环,所以从任何点出发往前走,必然终止于一个出度为0
的点)
• 1. 求出所有强连通分量
• 2. 每个强连通分量缩成一点,则形成一个有向无环图DAG。
• 3. DAG所有的点可达。那么该点所代表的连通分量上的所有的原图中
的点,都能被原图中的所有点可达,则该连通分量的点数,就是答案。
• 4. DAG上面如果有不止一个出度为0的点,则这些G上面如果有唯一的
出度为0的点,则该点能被点互相不可达,原问题无解,答案为0
• 缩点的时候不一定要构造新图,只要把不同强连通分量的点染不
同颜色,然后考察各种颜色的点有没有连到别的颜色的边即可(即
其对应的缩点后的DAG图上的点是否有出边)。
POJ-1236 Network of Schools
• N个学校之间有单向的网络,每个学校得到一套软件后,可以通
过单向网络向周边的学校传输。
• 问题1:初始至少需要向多少个学校发放软件,使得网络内所有
的学校最终都能得到软件。
• 问题2:至少需要添加几条传输线路(边),使任意向一个学校发放
软件后,经过若干次传送,网络内所有的学校最终都能得到软件。
• 2 < N <= 100
• 给定一个有向图,求:
• 1) 求一个最小的顶点集,使得从这个顶点集出发,可以到达全部顶点
• 2) 至少要加多少条边,才能从任何一个顶点出发,都能到达全部顶点
• N <= 100
有用的定理:
有向无环图中所有入度不为0的点,一定可以由
某个入度为0的点出发可达。
(由于无环,所以从任何入度不为0的点往回走,
必然终止于一个入度为0的点)
解题思路
1. 求出所有强连通分量
2. 每个强连通分量缩成一点,则形成一个有向无环图DAG。
3. DAG上面有多少个入度为0的顶点,问题1的答案就是多少
在DAG上要加几条边,才能使得DAG变成强连通的,问题2
的答案就是多少
加边的方法:
为每个入度为0的点添加入边,为每个出度为0的点添加出边
假定有 n 个入度为0的点, m个出度为0的点, max(m,n)就是
第二个问题的解(证明难,略)
Korasaju算法求有向图强连通分支
procedure Strongly_Connected_Components(G);
begin
1.深度优先遍历G,算出每个结点u的结束时间f[u],起
点如何选择无所谓。
2.深度优先遍历G的转置图GT, 选择遍历的起点时,
按照结点的结束时间从大到小进行。遍历的过程中,
一边遍历, 一边给结点做分类标记,每找到一个新的
起点,分类标记值就加1。
3. 第2步中产生的标记值相同的结点构成深度优先森
林中的一棵树,也即一个强连通分量
end;
证明参考:
http://www.bioisland.com/Algorithm/ShowArticle.asp?ArticleID=58
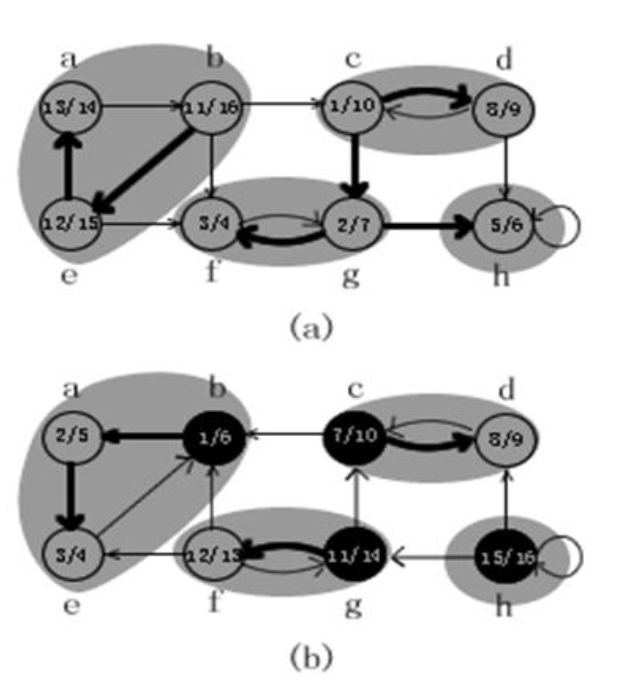
(a)为有向图G,其中的阴影部分是G
的强连通分支,对每个顶点都标出
了其发现时刻与完成时刻,黑色边
为深度优先搜索的树枝;
(b)G的转置图GT 依次以b,c,g,h为起
点做DFS, 得到4个强连通分量
算法复杂度分析
深度优先搜索的复杂度:Θ(V + E)
计算GT的复杂度:0或者Θ(V + E)(临接表)
所以总的复杂度为:Θ(V + E)
非常好的算法!
如果你不开心,那我就把右边 这个帅傻子分享给你吧,
这个帅傻子分享给你吧,
你看,他这么好看,跟个zz一样看着你,你还伤心吗?
真的!这照片盯上他五秒钟就想笑了。
一切都会过去的。
时间时间会给你答案2333

