P1096 Hanoi双塔问题
题目描述
给定 A 、 B 、 C 三根足够长的细柱,在 A 柱上放有 2n 个中间有孔的圆盘,共有 n 个不同的尺寸,每个尺寸都有两个相同的圆盘,注意这两个圆盘是不加区分的(下图为 n=3 的情形)。
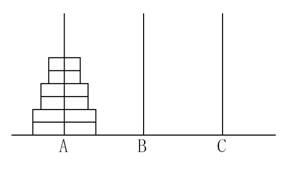
现要将这些圆盘移到 C 柱上,在移动过程中可放在 B 柱上暂存。要求:
(1)每次只能移动一个圆盘;
(2) A 、 B 、 C 三根细柱上的圆盘都要保持上小下大的顺序;
任务:设 An 为 2n 个圆盘完成上述任务所需的最少移动次数,对于输入的 n ,输出 An 。
输入输出格式
输入格式:
一个正整数 n ,表示在 A 柱上放有 2n 个圆盘。
输出格式:
一个正整数, 为完成上述任务所需的最少移动次数 An 。
输入输出样例
说明
【限制】
对于 50% 的数据, 1≤n≤25
对于 100% 的数据,1≤n≤200
【提示】
设法建立 An 与An−1 的递推关系式。
漫威系列二:
纯数学题,找规律。
比较懒,一开始,,感觉模拟那个过程太复杂了,
于是拿来了标程,从一到七跑了一遍。
是这样的:

清晰明了,看能不能找到规律。
规律来了,就是这样!:

ans答案一开始置为2,( 也就是 n ==1 时,ans = 2 )
n依次变大的话,就每次增加 2n ,厉不厉害!!!
然后就能直接写了。
根据规律直接写出来的代码应该是这样的:
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 8 int n; 9 long long m; 10 11 long long poww(int x,int y) 12 { 13 long long s=1; 14 for(int i=1;i<=y;++i) 15 s*=x; 16 return s; 17 } 18 19 int main() 20 { 21 scanf("%d",&n); 22 for(int i=1;i<=n;++i) 23 m+=poww(2,i); 24 printf("%lld",m); 25 }
哦,可惜因为精度范围问题拿不了满分。
比如一个样例数据:
input:
90
output:
2475880078570760549798248446
所以上面那个代码是不会输出这么大一个数的。
它会输出一个负数。
这时候就需要高精度了。
感觉无非就是将很大的数分离数位来记录。。
生产于本校的某大佬的正解思路是这样的:
原文:
“
先找出An的通项公式,而两个相同的圆盘移动方法和一个圆盘的移动方法差不多,
只要最后再乘二就好了,先考虑每种大小一个圆盘
而显然An=2*An-1+1,就相当于先把上面n-1个圆盘先挪走,再挪最大的,再把n-1个挪到它上面
又因为A1=1,因此有An=2^n-1,最后再乘二,An=2^(n+1)-2
写的话用高精度,算出2^(n+1),注意到2的幂的个位数字是2,4,8,6,所有再减二的时候不用考虑退位
”
所以ac代码:
#include<iostream> #include<cstdio> #include<cmath> #include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; int a[205]; int n,len,newl; int main() { scanf("%d",&n); a[1]=2; len=1; for(int j=1; j<=n; j++) { if(a[len]>=5) newl=len+1; else newl=len; for(int i=len; i>=1; i--) { a[i]=2*a[i]; if(a[i]>=10) { a[i+1]=a[i+1]+1; a[i]=a[i]-10; } } len=newl; } a[1]=a[1]-2; for(int i=len; i>=1; i--) printf("%d",a[i]); return 0; }
感兴趣的,大佬blog如下:
http://www.cnblogs.com/cangT-Tlan/p/8044788.html


