P1011 车站
洛谷——P1011 车站
题目描述
火车从始发站(称为第1站)开出,在始发站上车的人数为a,然后到达第2站,在第2站有人上、下车,但上、下车的人数相同,因此在第2站开出时(即在到达第3站之前)车上的人数保持为a人。从第3站起(包括第3站)上、下车的人数有一定规律:上车的人数都是前两站上车人数之和,而下车人数等于上一站上车人数,一直到终点站的前一站(第n-1站),都满足此规律。现给出的条件是:共有N个车站,始发站上车的人数为a,最后一站下车的人数是m(全部下车)。试问x站开出时车上的人数是多少?
输入输出格式
输入格式:
a(<=20),n(<=20),m(<=2000),和x(<=20),
输出格式:
从x站开出时车上的人数。
输入输出样例
输入样例#1:
5 7 32 4
输出样例#1:
13
sugar's blog:https://www.cnblogs.com/z360/p/6973082.html
但我怎么觉得她的表格有些问题呢。。。
思路:
话说这道题真心挺恶心,现推的时候还是挺麻烦的。。。
来吧,看下面表格。。。
在这个地方我们规定在第二站上车的人数为t。f[]为斐波那契数列前几项。
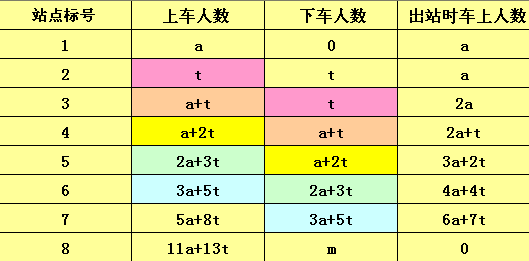
通过观察整个过程,你还会哦发现这样一个关系:
最后一站的人数m+第二站上车的人数等于倒数第二站上车的人数+第一站的人数。
即:m+t=f[n-1-2]*a+f[n-1-1]*t+a;
通过这个关系我们可以很快的求出t的值,
这样在第x站上车的人数等于:f[x-2]*a+f[x-1]*t;
在车上的人数等于:(f[x-2])*a+(f[x-1]+1)*t
思路对,代码对,其他的,自求多福。。
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #define N 1001 7 using namespace std; 8 int a,n,m,x,t,f[N]; 9 int main() 10 { 11 scanf("%d%d%d%d",&a,&n,&m,&x); 12 f[1]=1; 13 f[2]=1; 14 for(int i=3; i<=n; i++) 15 f[i]=f[i-1]+f[i-2]; 16 t=(m-(f[n-3]+1)*a)/(f[n-2]-1); 17 printf("%d",(f[x-2]+1)*a+(f[x-1]-1)*t); 18 return 0; 19 }
yes,
。。。


