初学积性函数
参考博客：①：http://jcvb.is-programmer.com/posts/41846.html ②：http://zhengyidong.me/2014/11/%E7%A7%AF%E6%80%A7%E5%87%BD%E6%95%B0%E7%B3%BB%E5%88%97%EF%BC%88%E4%B8%80%EF%BC%89%EF%BC%9A%E6%AC%A7%E6%8B%89%E5%87%BD%E6%95%B0/
一、
（一）
首先是积性函数的定义：
定义在正整数集（自变量n ∈ Z*）上的函数 f（n） （称为算术函数），若 gcd（a，b）= 1 （a，b的最大公约数为1，也就是说a，b互为质数）时有（若） f（a）f（b）= f（ab），则（那么）f（x）称为积性函数。
然后有一个显然的性质：（非恒等于零的）（保证这个函数不会恒等于零，那么这个）积性函数 f（n）必然满足 f（1）= 1。
（二）
定义逐点加法（规定，只是一个定义）：( f + g ) ( x ) = f ( x ) + g ( x ) , ( f · g ) ( x ) = f ( x ) g ( x ) ;
也就是说另（设）( f + g ) ( x ) = f ( x ) + g ( x ) , ( f · g ) ( x ) = f ( x ) g ( x ) 这么两个式子成立。（不必深究，自己去搜证明）
又一个比较显然的性质（根据逐点加法）：若 f ，g（ f（ x ）和 g（ x ））均为积性函数，则 f · g （ f（ x ）· g（ x ））也是积性函数。
（三）
有用的：https://wenda.so.com/q/1435082634723576?src=150 https://baike.so.com/doc/6700501-6914434.html
积性函数的求值: n = ∏piai ,则 f(n) = ∏f(piai)，所以只要解决 n = pa 时 f(n)的值即可（看两个式子的区别，悟）。
（四）
完全积性函数：
完全积性函数是指所有对于任何a,b都有性质f(ab)=f(a)f(b)的数论函数。
对于整数n的一个数论函数 f(n)，若f(1)=1，且当a,b互质时f(ab)=f(a)f(b)，在数论上就称它为积性函数。（上边定义）
若对于某积性函数 f(n)（已经是积性函数） ，就算a, b不互质，也有f(ab)=f(a)f(b)，则称它为完全积性的。
（五）
进一步理解：
很容易发现一些常见函数 f（ n ）= 1 ，f（ n ）= n ，f（ n ）= n * n 等都是积性函数。
事实上所有的幂函数都是积性函数。
二、
（一）
一些性质：
交换律 f * g = g * f ,
结合律( f * g ) * h = f * ( g * h ) ,
对逐点加法的分配律 f * ( g + h ) = f * g + f * h ;
重要性质①：
若 f，g 均为积性函数，则 f * g也是积性函数。（展开式子即可证明）
n的约数（短除，整除数）个数d（n）可以写成 d（ n ）= （1 * 1 ）（ n ）；约数和σ（n）；
可以写成σ (n) = (1 * id) (n) ，
由上面的性质可知（也就是说如果有一个函数f（x），如果f（x）=（a*b）（c*d）……（共有x的所有除数个“（）”））
那么这两个函数均是积性函数。
重要性质②：
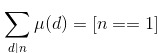，即1*μ=e。（可用二项式定理证明）；
重要性质③：
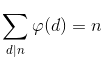，即1*φ=id。（n是质数时显然成立，再由积性得证）；
感性理解。
