20170903四校联考
之前0827的联考因为某砖暂停了,让我多活了一周233
T1:
题目描述
上体育课的时候,小蛮的老师经常带着同学们一起做游戏。这次,老师带着同学们一起做传球游戏。
游戏规则是这样的:n个同学站成一个圆圈,其中的一个同学手里拿着一个球,当老师吹哨子时开始传球,每个同学可以把球传给自己左右的两个同学中的一个(左右任意),当老师在此吹哨子时,传球停止,此时,拿着球没有传出去的那个同学就是败者,要给大家表演一个节目。
聪明的小蛮提出一个有趣的问题:有多少种不同的传球方法可以使得从小蛮手里开始传的球,传了m次以后,又回到小蛮手里。两种传球方法被视作不同的方 法,当且仅当这两种方法中,接到球的同学按接球顺序组成的序列是不同的。比如有三个同学1号、2号、3号,并假设小蛮为1号,球传了3次回到小蛮手里的方式有1->2->3->1和1->3->2->1,共2种。
输入格式:
输入文件ball.in共一行,有两个用空格隔开的整数n,m(2<=n<=1000,1<=m<=10^9)。
输出格式:
输出文件ball.out共一行,有一个整数,表示符合题意的方法数。
题解:
f[i][j]=f[(i+1)%n][j-1]+f[(i-1+n)%n][j-1];
f[0][0]=1;
f[0][m]为结果
这都是垃圾PJ组2008的方程,但是在这一题不适用。
留意到n的范围较小,可以得出如果用矩阵优化,可以达到O(n^2)的效率。
因为m的范围太大,必须刚快速幂。
注意到初始矩阵是一个循环矩阵,所以每次乘出来的矩阵都是循环矩阵,可以直接O(n^2)递推
所以就这样奇妙的过了,真开心!
代码:

#include<cstdio> #include<cstring> #define r register #define Fn "ball" typedef long long ll; #define mod 1000000007ll #define sz 1005 typedef ll arr[sz][sz]; arr s,a,t; int n,m; inline void qpow(){ for(r int i=1;i<=n;i++)a[i][i]=1; while(m){ if(m&1){ memset(t,0,sizeof(t)); for(r int i=1;i<=n;i++) for(r int j=1;j<=n;j++) t[1][i]=(t[1][i]+a[1][j]*s[j][i])%mod; for(r int i=2;i<=n;i++){ t[i][1]=t[i-1][n]; for(r int j=2;j<=n;j++)t[i][j]=t[i-1][j-1]; } memcpy(a,t,sizeof(arr)); } memset(t,0,sizeof(t)); for(r int i=1;i<=n;i++) for(r int j=1;j<=n;j++) t[1][i]=(t[1][i]+s[1][j]*s[j][i])%mod; for(r int i=2;i<=n;i++){ t[i][1]=t[i-1][n]; for(r int j=2;j<=n;j++)t[i][j]=t[i-1][j-1]; } memcpy(s,t,sizeof(arr)); m>>=1; } } int main(){ freopen(Fn".in","r",stdin); freopen(Fn".out","w",stdout); scanf("%d%d",&n,&m); s[1][2]=s[1][n]=1; for(r int i=2;i<=n;i++){ s[i][1]=s[i-1][n]; for(r int j=2;j<=n;j++)s[i][j]=s[i-1][j-1]; } qpow(); printf("%d\n",a[1][1]); return 0; }
T3:
与
【问题描述】
给定𝑛个非负整数a3, 𝑎5, … , 𝑎7 ,你需要求出有多少种方法可以将它们分成两 部分,使得两部分都至少有一个数,并且两部分的数进行按位与操作后的结果
相同。
按位与是一种对于二进制数的操作,它等价于 C / C + + 里的运算 & 和 Pascal里的运算 and 。即,将两个数写成二进制,较短的数补前导零使得两个 数一样长。然后如果两个数在某一位上都是1,那么这一位运算的结果为1;否 则这一位为 0 。例如两个整数14 和11,它们按位与运算后的结果应为10 。
【输入文件】
输入文件的第一行为一个正整数𝑛。第二行为𝑛个非负整数𝑎3, 𝑎5, … , 𝑎7。
【输出文件】
输出为一行一个整数,表示合法的方案数。
题解:
容斥原理!!!!!!!计数问题都得打容斥原理!!!!!!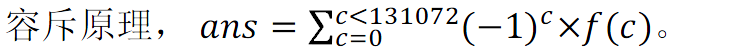
其中变量𝑐枚举的是子集,代表需要限制为不符合要求的二进制位(就是这 些位一定得一边是0一边是1)。𝑓(𝑐)指在𝑐的限制下的方案数。
由于有一些位一定得一边是0一边是1,所以这些位为1的元素一定得归一边,可以考虑把它们合并为一个元素。如果有多个位有限制,那就用并查集来合并元素。合并完以后的计算就非常容易了。
如果所有元素的某一位上全部都是0或1,在实际计算的时候应该稍微特判 一下。或者可以考虑把所有全部相同的位直接去掉,这样一定不会影响答案,又可以避免特殊情况的出现。
代码:

#include<cstdio> #define r register #define Fn "and" typedef long long ll; ll b[65]={1},ans; int fa[65],a[65]; inline int read(){ r int x=0,f=1;r char c=getchar(); for(;c<'0'||c>'9';f=c=='-'?-1:1,c=getchar()); for(;c>='0'&&c<='9';x=(x<<3)+(x<<1)+c-'0',c=getchar()); return x*f; } inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);} int main(){ freopen(Fn".in","r",stdin); freopen(Fn".out","w",stdout); int n=read(); for(r int i=1;i<=n;i++)a[i]=read(); for(r int i=1;i<62;i++)b[i]=b[i-1]<<1; for(r int i=0;i<131072;i++){ r int t=i,ti=1,cnt=0; for(r int j=1;j<=n;j++)fa[j]=j; for(;cnt<17;cnt++,t>>=1) if(t&1){ ti*=-1; r int tmp=(int)b[cnt],tmp2=0,flag=0; for(r int k=1;k<=n;k++) if(!(a[k]&tmp))flag=1,tmp2?fa[find(k)]=tmp2:tmp2=find(k); if(!flag)break; } if(cnt!=17)continue; r int sum=0; for(r int j=1;j<=n;j++)sum+=find(j)==j; ans+=(b[sum]-2)*ti; } printf("%I64d\n",ans); return 0; }
由于时间原因,T2的代码尚未打完,请各位大佬Czhou谅解!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号