玩转数据结构：第6章 二分搜索树

二分搜索树

---

6-1 为什么要研究树结构

树结构

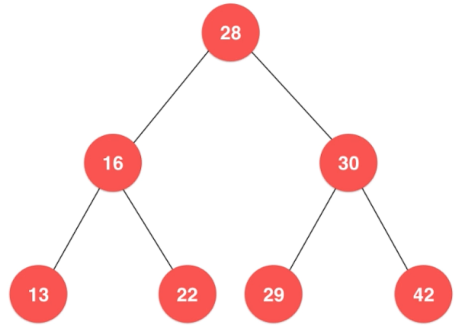
为什么要有树结构？

• 树结构本身是一种天然的组织结构
• 高效

 

将数据使用树结构存储后，出奇的高效。

• 二分搜索树（Binary Search Tree）
• 平衡二叉树：AVL；红黑树
• 堆；并查集
• 线段树；Trie(字典树，前缀树)

6-2 二分搜索树基础

和链表一样，动态数据结构。

二叉树，具有天然递归结构。

• 每个节点的左子树也是二叉树
• 每个节点的右子树也是二叉树

•  二叉树每个节点最多有一个父亲

二分搜索树 Binary Search Tree

二分搜索树是二叉树

二分搜索树，存储的元素必须有可比较性。

BST.java

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }
}

6-3 向二分搜索树中添加元素

03-Add-Elements-in-BST

BST.java

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){

        if(root == null){
            root = new Node(e);
            size ++;
        }
        else
            add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    private void add(Node node, E e){
        if(e.equals(node.e))
            return;
        else if(e.compareTo(node.e) < 0 && node.left == null){
            node.left = new Node(e);
            size ++;
            return;
        }
        else if(e.compareTo(node.e) > 0 && node.right == null){
            node.right = new Node(e);
            size ++;
            return;
        }

        if(e.compareTo(node.e) < 0)
            add(node.left, e);
        else //e.compareTo(node.e) > 0
            add(node.right, e);
    }
}

6-4 改进添加操作：深入理解递归终止条件

04-Improved-Add-Elements-in-BST

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }
}

6-5 二分搜索树的查询操作

05-Search-in-BST

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }
}

6-6 二分搜索树的前序遍历

06-PreOrder-Traverse-in-BST

public class Main {

    public static void main(String[] args) {

        BST<Integer> bst = new BST<>();
        int[] nums = {5, 3, 6, 8, 4, 2};
        for(int num: nums)
            bst.add(num);

        /////////////////
        //      5      //
        //    /   \    //
        //   3    6    //
        //  / \    \   //
        // 2  4     8  //
        /////////////////
        bst.preOrder();
        System.out.println();

        System.out.println(bst);
    }
}

BST.java

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){
        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e + "\n");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}

6-7 二分搜索树的中序遍历和后序遍历

07-InOrder-and-PostOrder-Traverse-in-BST

public class Main {

    public static void main(String[] args) {

        BST<Integer> bst = new BST<>();
        int[] nums = {5, 3, 6, 8, 4, 2};
        for(int num: nums)
            bst.add(num);

        /////////////////
        //      5      //
        //    /   \    //
        //   3    6    //
        //  / \    \   //
        // 2  4     8  //
        /////////////////
        bst.preOrder();
        System.out.println();

        bst.inOrder();
        System.out.println();

        bst.postOrder();
        System.out.println();
    }
}

BST.java

import java.util.Stack;

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){
        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node){
        if(node == null)
            return;

        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    // 后序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node){
        if(node == null)
            return;

        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e + "\n");
        generateString(node.left, depth + 1, res);
        generateString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}

6-8 深入理解二分搜索树的前中后序遍历 

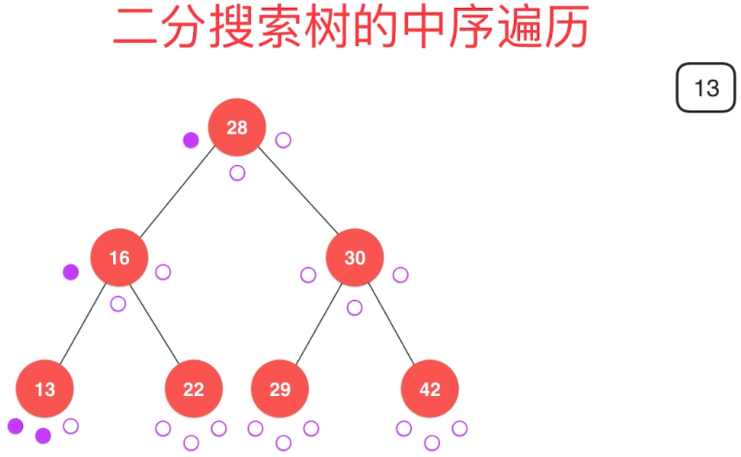
6-9 二分搜索树前序遍历的非递归实现

/// Leetcode 144. Binary Tree Preorder Traversal
/// https://leetcode.com/problems/binary-tree-preorder-traversal/description/

09-Non-Recursion-Preorder-Traverse-in-BST 

public class Main {

    public static void main(String[] args) {

        BST<Integer> bst = new BST<>();
        int[] nums = {5, 3, 6, 8, 4, 2};
        for(int num: nums)
            bst.add(num);

        /////////////////
        //      5      //
        //    /   \    //
        //   3    6    //
        //  / \    \   //
        // 2  4     8  //
        /////////////////
        bst.preOrder();
        System.out.println();

        bst.preOrderNR();
        System.out.println();
    }
}

BST.java

import java.util.Stack;

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){
        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    // 二分搜索树的非递归前序遍历
    public void preOrderNR(){

        if(root == null)
            return;

        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            Node cur = stack.pop();
            System.out.println(cur.e);

            if(cur.right != null)
                stack.push(cur.right);
            if(cur.left != null)
                stack.push(cur.left);
        }
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e + "\n");
        generateString(node.left, depth + 1, res);
        generateString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}

Solution

/// Leetcode 144. Binary Tree Preorder Traversal
/// https://leetcode.com/problems/binary-tree-preorder-traversal/description/
///
/// 课程中在这里暂时没有介绍这个问题
/// 该代码主要用于使用Leetcode上的问题测试我们的BST类
/// 该测试主要测试前序遍历的非递归写法

import java.util.List;
import java.util.LinkedList;
import java.util.Stack;

public class Solution {

    // Definition for a binary tree node.
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
    }

    public List<Integer> preorderTraversal(TreeNode root) {

        List<Integer> res = new LinkedList<>();
        if(root == null)
            return res;

        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode cur = stack.pop();
            res.add(cur.val);

            if(cur.right != null)
                stack.push(cur.right);
            if(cur.left != null)
                stack.push(cur.left);
        }

        return res;
    }
}

遍历过程中一扎到底，就是所谓的“深度优先遍历”

 6-10 二分搜索树的层序遍历

10-Level-Traverse-in-BST 

public class Main {

    public static void main(String[] args) {

        BST<Integer> bst = new BST<>();
        int[] nums = {5, 3, 6, 8, 4, 2};
        for(int num: nums)
            bst.add(num);

        /////////////////
        //      5      //
        //    /   \    //
        //   3    6    //
        //  / \    \   //
        // 2  4     8  //
        /////////////////
        bst.preOrder();
        System.out.println();

        bst.inOrder();
        System.out.println();

        bst.postOrder();
        System.out.println();

        bst.levelOrder();
        System.out.println();
    }
}

BST.java

import java.util.Stack;
import java.util.Queue;
import java.util.LinkedList;

public class BST<E extends Comparable<E>> {

    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){
        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    // 二分搜索树的非递归前序遍历
    public void preOrderNR(){

        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            Node cur = stack.pop();
            System.out.println(cur.e);

            if(cur.right != null)
                stack.push(cur.right);
            if(cur.left != null)
                stack.push(cur.left);
        }
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node){
        if(node == null)
            return;

        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    // 后序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node){
        if(node == null)
            return;

        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

    // 二分搜索树的层序遍历
    public void levelOrder(){

        if(root == null)
            return;

        Queue<Node> q = new LinkedList<>();
        q.add(root);
        while(!q.isEmpty()){
            Node cur = q.remove();
            System.out.println(cur.e);

            if(cur.left != null)
                q.add(cur.left);
            if(cur.right != null)
                q.add(cur.right);
        }
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e + "\n");
        generateString(node.left, depth + 1, res);
        generateString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}

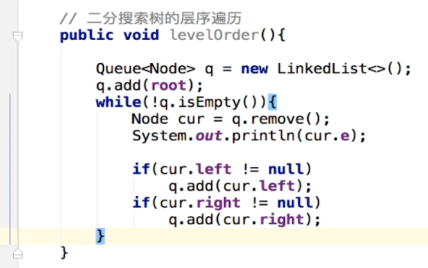
广度优先遍历的意义

常用于算法设计中——最短路径，更快的找到问题的解

6-11 删除二分搜索树的最大元素和最小元素

11-Remove-Min-and-Max-in-BST

import java.util.ArrayList;
import java.util.Random;

public class Main {

    public static void main(String[] args) {

        BST<Integer> bst = new BST<>();
        Random random = new Random();

        int n = 1000;

        // test removeMin
        for(int i = 0 ; i < n ; i ++)
            bst.add(random.nextInt(10000));

        ArrayList<Integer> nums = new ArrayList<>();
        while(!bst.isEmpty())
            nums.add(bst.removeMin());

        System.out.println(nums);
        for(int i = 1 ; i < nums.size() ; i ++)
            if(nums.get(i - 1) > nums.get(i))
                throw new IllegalArgumentException("Error!");
        System.out.println("removeMin test completed.");


        // test removeMax
        for(int i = 0 ; i < n ; i ++)
            bst.add(random.nextInt(10000));

        nums = new ArrayList<>();
        while(!bst.isEmpty())
            nums.add(bst.removeMax());

        System.out.println(nums);
        for(int i = 1 ; i < nums.size() ; i ++)
            if(nums.get(i - 1) < nums.get(i))
                throw new IllegalArgumentException("Error!");
        System.out.println("removeMax test completed.");
    }
}

BST.java

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class BST<E extends Comparable<E>> {

    private class Node{
        public E e;
        public Node left, right;

        public Node(E e){
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){

        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){

        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    // 二分搜索树的非递归前序遍历
    public void preOrderNR(){

        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            Node cur = stack.pop();
            System.out.println(cur.e);

            if(cur.right != null)
                stack.push(cur.right);
            if(cur.left != null)
                stack.push(cur.left);
        }
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node){

        if(node == null)
            return;

        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    // 后序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node){

        if(node == null)
            return;

        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

    // 二分搜索树的层序遍历
    public void levelOrder(){

        Queue<Node> q = new LinkedList<>();
        q.add(root);
        while(!q.isEmpty()){
            Node cur = q.remove();
            System.out.println(cur.e);

            if(cur.left != null)
                q.add(cur.left);
            if(cur.right != null)
                q.add(cur.right);
        }
    }

    // 寻找二分搜索树的最小元素
    public E minimum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty");

        Node minNode = minimum(root);
        return minNode.e;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if( node.left == null )
            return node;

        return minimum(node.left);
    }

    // 寻找二分搜索树的最大元素
    public E maximum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty");

        return maximum(root).e;
    }

    // 返回以node为根的二分搜索树的最大值所在的节点
    private Node maximum(Node node){
        if( node.right == null )
            return node;

        return maximum(node.right);
    }

    // 从二分搜索树中删除最小值所在节点, 返回最小值
    public E removeMin(){
        E ret = minimum();
        root = removeMin(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){

        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }

    // 从二分搜索树中删除最大值所在节点
    public E removeMax(){
        E ret = maximum();
        root = removeMax(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMax(Node node){

        if(node.right == null){
            Node leftNode = node.left;
            node.left = null;
            size --;
            return leftNode;
        }

        node.right = removeMax(node.right);
        return node;
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e +"\n");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}

 6-12 删除二分搜索树的任意元素

12-Remove-Elements-in-BST

import java.util.ArrayList;
import java.util.Random;

public class Main {

    // 打乱数组顺序
    private static void shuffle(Object[] arr){

        for(int i = arr.length - 1 ; i >= 0 ; i --){
            int pos = (int) (Math.random() * (i + 1));
            Object t = arr[pos];
            arr[pos] = arr[i];
            arr[i] = t;
        }
    }

    public static void main(String[] args) {

        BST<Integer> bst = new BST<>();
        Random random = new Random();

        int n = 10000;

        for(int i = 0 ; i < n ; i ++)
            bst.add(random.nextInt(n));

        // 注意, 由于随机生成的数据有重复, 所以bst中的数据数量大概率是小于n的

        // order数组中存放[0...n)的所有元素
        Integer[] order = new Integer[n];
        for( int i = 0 ; i < n ; i ++ )
            order[i] = i;
        // 打乱order数组的顺序
        shuffle(order);

        // 乱序删除[0...n)范围里的所有元素
        for( int i = 0 ; i < n ; i ++ )
            if(bst.contains(order[i])){
                bst.remove(order[i]);
                System.out.println("After remove " + order[i] + ", size = " + bst.size() );
            }

        // 最终整个二分搜索树应该为空
        System.out.println(bst.size());
    }
}

BST.java

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class BST<E extends Comparable<E>> {

    private class Node{
        public E e;
        public Node left, right;

        public Node(E e){
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }

    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){

        if(node == null){
            size ++;
            return new Node(e);
        }

        if(e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if(e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e, 递归算法
    private boolean contains(Node node, E e){

        if(node == null)
            return false;

        if(e.compareTo(node.e) == 0)
            return true;
        else if(e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 前序遍历以node为根的二分搜索树, 递归算法
    private void preOrder(Node node){

        if(node == null)
            return;

        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    // 二分搜索树的非递归前序遍历
    public void preOrderNR(){

        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            Node cur = stack.pop();
            System.out.println(cur.e);

            if(cur.right != null)
                stack.push(cur.right);
            if(cur.left != null)
                stack.push(cur.left);
        }
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 中序遍历以node为根的二分搜索树, 递归算法
    private void inOrder(Node node){

        if(node == null)
            return;

        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    // 后序遍历以node为根的二分搜索树, 递归算法
    private void postOrder(Node node){

        if(node == null)
            return;

        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

    // 二分搜索树的层序遍历
    public void levelOrder(){

        Queue<Node> q = new LinkedList<>();
        q.add(root);
        while(!q.isEmpty()){
            Node cur = q.remove();
            System.out.println(cur.e);

            if(cur.left != null)
                q.add(cur.left);
            if(cur.right != null)
                q.add(cur.right);
        }
    }

    // 寻找二分搜索树的最小元素
    public E minimum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty!");

        return minimum(root).e;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null)
            return node;
        return minimum(node.left);
    }

    // 寻找二分搜索树的最大元素
    public E maximum(){
        if(size == 0)
            throw new IllegalArgumentException("BST is empty");

        return maximum(root).e;
    }

    // 返回以node为根的二分搜索树的最大值所在的节点
    private Node maximum(Node node){
        if(node.right == null)
            return node;

        return maximum(node.right);
    }

    // 从二分搜索树中删除最小值所在节点, 返回最小值
    public E removeMin(){
        E ret = minimum();
        root = removeMin(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){

        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }

    // 从二分搜索树中删除最大值所在节点
    public E removeMax(){
        E ret = maximum();
        root = removeMax(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMax(Node node){

        if(node.right == null){
            Node leftNode = node.left;
            node.left = null;
            size --;
            return leftNode;
        }

        node.right = removeMax(node.right);
        return node;
    }

    // 从二分搜索树中删除元素为e的节点
    public void remove(E e){
        root = remove(root, e);
    }

    // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    private Node remove(Node node, E e){

        if( node == null )
            return null;

        if( e.compareTo(node.e) < 0 ){
            node.left = remove(node.left , e);
            return node;
        }
        else if(e.compareTo(node.e) > 0 ){
            node.right = remove(node.right, e);
            return node;
        }
        else{   // e.compareTo(node.e) == 0

            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }

            // 待删除节点右子树为空的情况
            if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }

            // 待删除节点左右子树均不为空的情况

            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;

            node.left = node.right = null;

            return successor;
        }
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e +"\n");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}