[模式识别复习笔记] 第9章 神经网络及BP算法

1. 基本概念

1.1 神经元

神经网络是很多的 神经元 模型按照一定的层次结构连接起来所构成的。

---

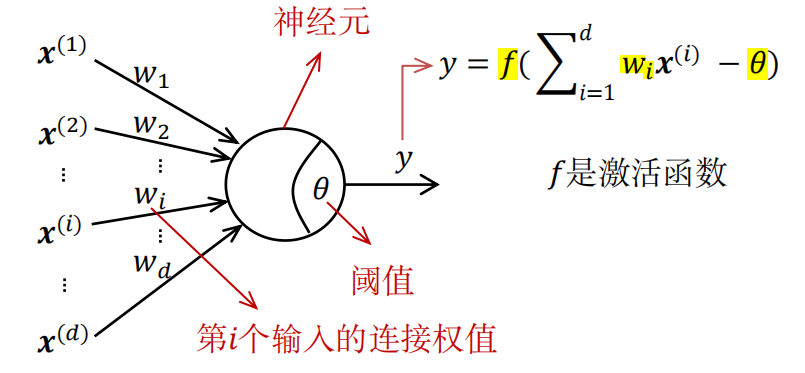
1.2 激活函数

• \(\text{ReLU}\) 函数：修正线性单元ReLU，是一种人工神经网络中常用的激活函数。

  \[\text{ReLU}(x) = \max(0, x) \]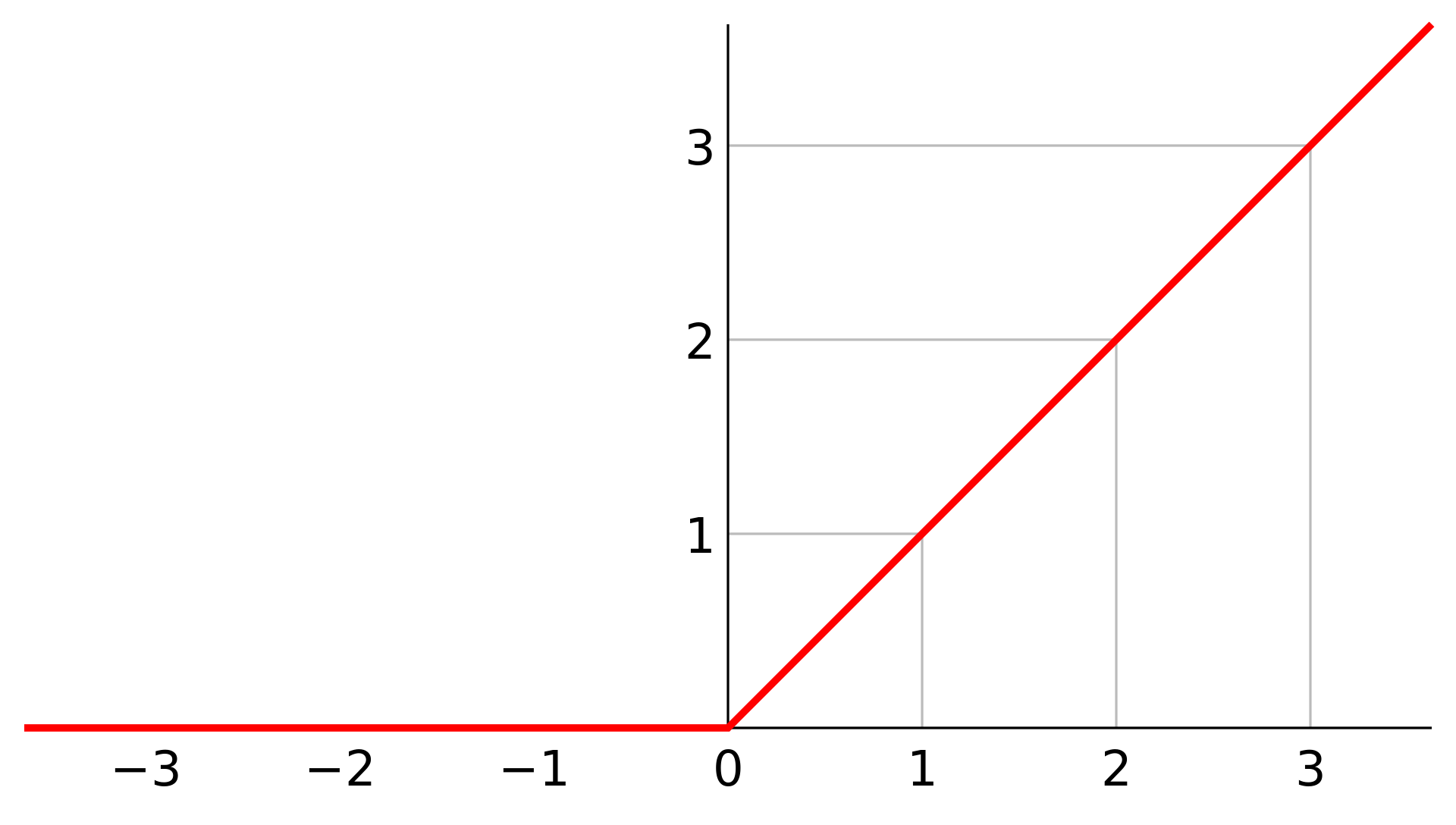
  

• \(\text{sgn}\) 阶跃函数：它将输入值映射为 \(0\) 或 \(1\)，\(0\) 表示抑制神经元，\(1\) 表示激活神经元。阶跃函数不连续、不光滑。

  \[\text{sgn}(x) = \begin{cases} 1, & x \ge 0 \\\\ 0, & x < 0 \end{cases} \]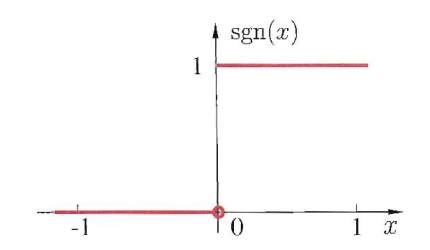
  

• \(\text{sigmoid}\) 函数：将值映射到 \((0,1)\) 范围内。该函数连续、光滑、单调。

  \[\text{sigmoid}(x) = \frac{1}{1 + e^{-x}} \]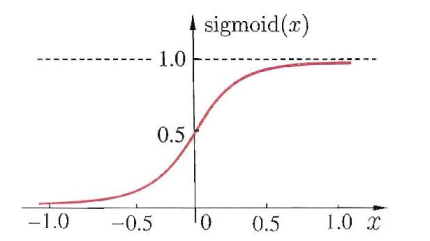
  
  
  

  \(\text{sigmoid}(x)\) 的导数为 \(f(x)(1 - f(x))\):

  证明：

  \(\text{sigmoid}\) 函数如下：

  \[f(x) = \frac{1}{1 + e^{-x}} \]

  我们先对其进行变形，得：

  \[\begin{split} f(x) &= \frac{1}{1 + e^{-x}} \\\\ &= \frac{e^x}{e^x + 1} \\\\ &= 1 - (e^x + 1)^{-1} \end{split} \]

  由此可得 \(\text{sigmoid}\) 的导数如下：

  \[\begin{split} \frac{\text{d} f}{\text{d} x} &= (e^x + 1)^{-2} e^x \\\\ &= [e^x(1 + e^{-x})]^{-2} e^x \\\\ &= (1 + e^{-x})^{-2} e^{-2x} e^x \\\\ &= (1 + e^{-x})^{-1} \; \frac{e^{-x}}{1 + e^{-x}} \\\\ &= f(x) \; (1 - f(x)) \end{split} \]

  我们可以再看下 \(f(-x)\) 的导数。显然 \(\text{sigmoid}\) 函数满足 \(f(-x) = 1 - f(x)\)，所以\(f(-x)\) 的导数就很简单了，就是 \(-f(x)(1 - f(x))\)。

---

1.3 网络结构

感知机 是模拟 单个神经元 功能的一种数学模型，只能用于求解线性可分的问题。

根据神经元连接方式和信息传递方向，神经网络可以划分为 前馈型网络 和 反馈型网络 两大类。本章的学习主要还是 前馈型网络。

在前馈型网络中，神经元有明显的层次结构，每层的神经元与下一层神经元 全互联。

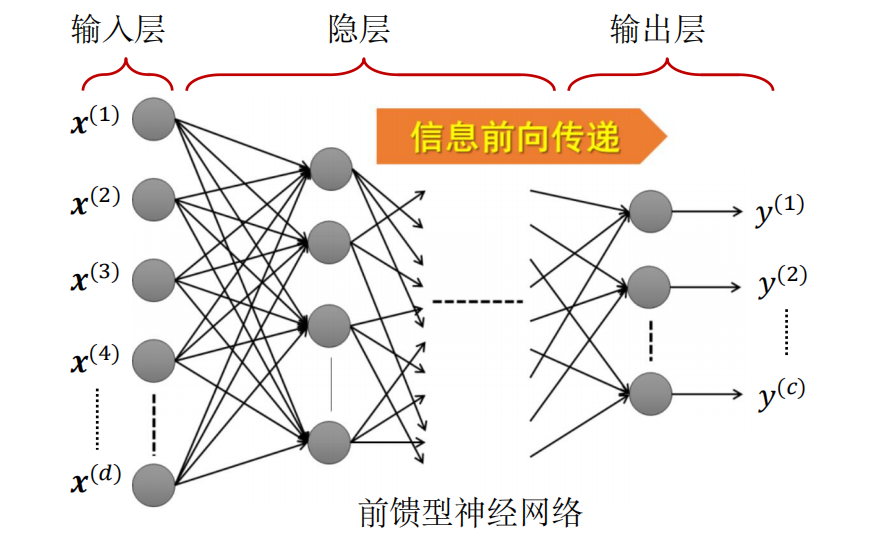
在前馈神经网络中：输入层神经元仅接收外界输入，不对输入进行处理；隐层和输出层神经元：是拥有激活函数的功能神经元，负责对输入进行加工，最终结果由输出层神经元输出。

---

1.4 网络训练

确定使用神经网络作为模式识别的算法后，需要：

• 设计网络结构：包括网络层数、每层神经元的个数、神经元之间的连接关系，神经元采用的激活函数形式。

• 训练网络参数：使用训练数据集学习得到神经元之间的连接权值和功能神经元的阈值。

神经网络的训练/学习过程，就是根据训练数据来调整 神经元之间的连接权 以及 每个功能神经元的阈值（阈值和偏置项本质是一个东西）。

---

2. BP算法

2.1 算法简介

误差反向传播(error BackPropagation，简称 BP) 算法是最常用的神经网络学习/训练算法。

给定一个训练集 \(\{ (\bm{x}_1, \bm{y}_1), \ldots, (\bm{x}_N, \bm{y}_N) \}\)，其中 \(\bm{x}_t \in \mathbb{R}^{d}, \bm{y}_t \in \mathbb{R}^{c}\)。

\(\bm{y}_t\) 是第 \(t\) 个样本 \(\bm{x}_t\) 的类标 \(\text{one-hot}\) 向量。向量中哪一个维度为 \(1\)，表示这个样本被分到哪一类。

---

2.2 结构与符号表示

---

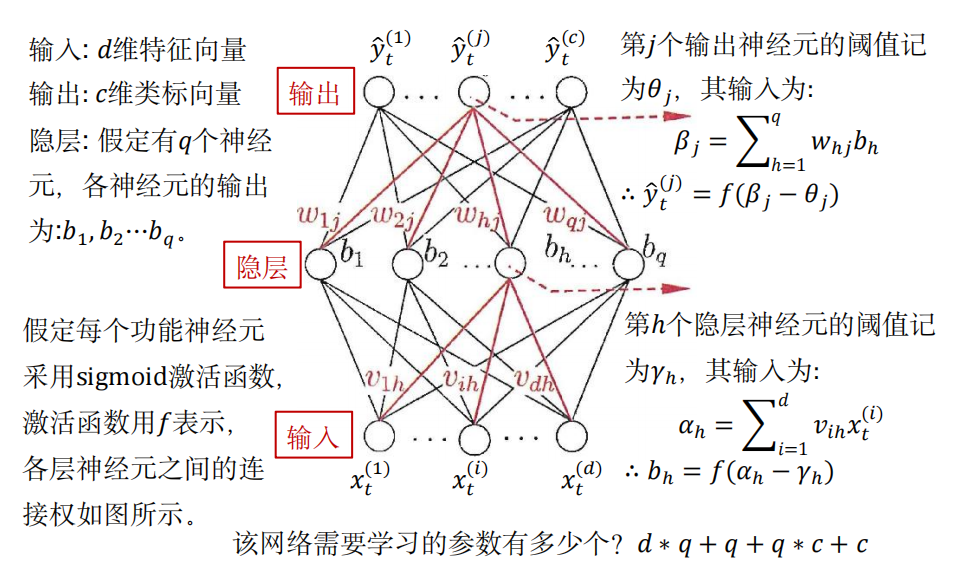
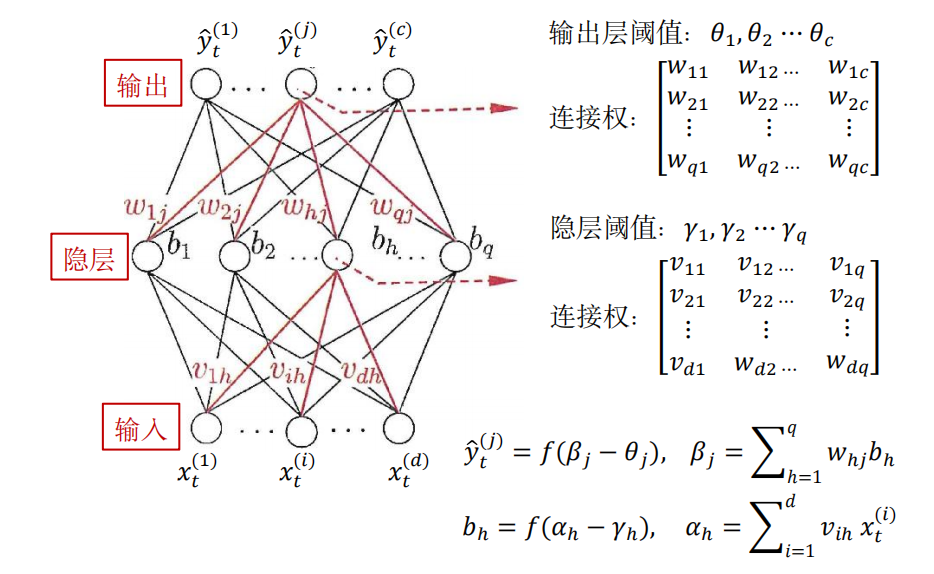
2.3 算法原理

\(\text{BP}\) 算法是为了找到一组最优网络参数，最小化全体样本上的训练误差:

\[E_t = \frac{1}{2}\sum_{i=1}^{N}||\hat{\bm{y}}_t - \bm{y}_t||^2 = \frac{1}{2}\sum_{j=1}^c (\hat{y}_t^{(j)} - y_t^{(j)})^2 \]

其中 \(\hat{\bm{y}}_t\) 是网络对 \(\bm{x}_t\) 的预测（对于一个 \(c\) 类的分类问题，在前向传播得到的 \(\hat{\bm{y}}_t\) 中 最大元素对应的类别 就是 预测的类别）；\(\bm{y}_t\) 是理想的输出。

BP算法通常采用 “随机梯度下降” (SGD) 算法最小化在当前样本上的训练误差。每次迭代调整网络参数 \(u\):

\[u \leftarrow u - \eta \frac{\partial E_t}{\partial u} \]

其中 \(\eta\) 为学习率。

---

2.4 参数更新推导

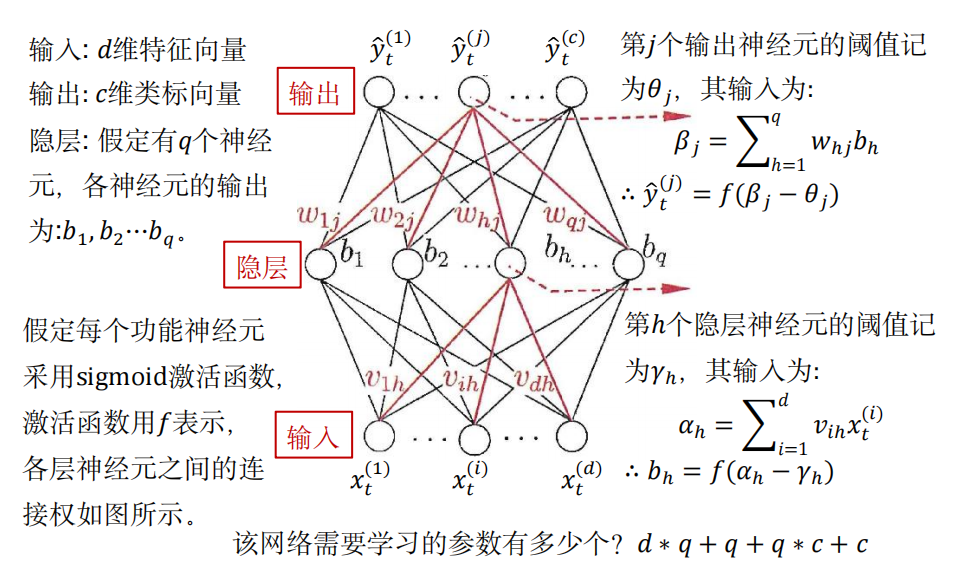
对 输出层第 \(j\) 个神经元的阈值：\(\theta_j \rightarrow \hat{y}_t^{(j)} \rightarrow E_t\)

由链式求导法则：

\[\frac{\partial E_t}{\partial \theta_j} = \frac{\partial E_t}{\partial \hat{y}_t^{(j)}} \cdot \frac{\partial \hat{y}_t^{(j)}}{\partial \theta_j} = (\hat{y}_t^{(j)} - y_t^{(j)}) \cdot \frac{\partial \hat{y}_t^{(j)}}{\partial \theta_j} \]

由 \(f(x) = \frac{1}{1 + e^{-x}}\) 函数导数为 \(f(x)(1 - f(x))\):

\[\frac{\partial E_t}{\partial \theta_j} = - (\hat{y}_t^{(j)} - y_t^{(j)}) \hat{y}_t^{(j)} (1 - \hat{y}_t^{(j)}) = -g_j \]

---

对 隐层 的 第 \(h\) 个神经元 到 输出层 的 第 \(j\) 个神经元的连接权值：\(w_{hj} \rightarrow \beta_j \rightarrow \hat{y}_t^{(j)} \rightarrow E_t\)

由链式求导法则：

\[\frac{\partial E_t}{\partial w_{hj}} = \frac{\partial E_t}{\partial \hat{y}_t^{(j)}}\cdot \frac{\partial \hat{y}_t^{(j)}}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial w_{hj}} \]

由 \(\hat{y}_t^{(j)} = f(\beta_j - \theta_j), \beta_j = \sum_{h=1}^{q} w_{hj}b_h\):

\[\frac{\partial E_t}{\partial w_{hj}} = (\hat{y}_t^{(j)} - y_t^{(j)}) \hat{y}_t^{(j)} (1 - \hat{y}_t^{(j)}) b_h = g_j b_h \]

---

对 隐层 的 第 \(h\) 个神经元的阈值：

\[\gamma_h \rightarrow b_h \rightarrow \begin{cases} \beta_1 \rightarrow \hat{y}_t^{(1)} \\\\ \vdots \\\\ \beta_c \rightarrow \hat{y}_t^{(c)} \end{cases} \Rightarrow E_t \]

由链式求导法则：

\[\frac{\partial E_t}{\partial \gamma_{h}} = \sum_{j=1}^{c} \frac{\partial E_t}{\partial \hat{y}_t^{(j)}}\cdot \frac{\partial \hat{y}_t^{(j)}}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial b_h} \cdot \frac{\partial b_h}{\partial \gamma_h} \]

由 \(\frac{\partial E_t}{\partial \hat{y}_t^{(j)}}\cdot \frac{\partial \hat{y}_t^{(j)}}{\partial \beta_j} = g_j\)，\(\frac{\partial \beta_j}{\partial b_h} = w_{hj}\)，\(\frac{\partial b_h}{\partial \gamma_h} = -b_h(1 - b_h)\):

\[\frac{\partial E_t}{\partial \gamma_{h}} = -b_h(1 - b_h)\sum_{j=1}^{c}g_j w_{hj} = -e_h \]

---

对 输入层 第 \(i\) 个神经元 到 隐层第 \(h\) 个神经元的连接权值:

\[v_{ih} \rightarrow \alpha_h \rightarrow b_h \rightarrow \begin{cases} \beta_1 \rightarrow \hat{y}_t^{(1)} \\\\ \vdots \\\\ \beta_c \rightarrow \hat{y}_t^{(c)} \end{cases} \Rightarrow E_t \]

由链式求导法则：

\[\frac{\partial E_t}{\partial v_{ih}} = \sum_{j=1}^{c} \frac{\partial E_t}{\partial \hat{y}_t^{(j)}}\cdot \frac{\partial \hat{y}_t^{(j)}}{\partial \beta_j} \cdot \frac{\partial \beta_j}{\partial b_h} \cdot \frac{\partial b_h}{\partial \alpha_h}\cdot \frac{\partial \alpha_h}{\partial v_{ih}} \]

由 \(\frac{\partial E_t}{\partial \hat{y}_t^{(j)}}\cdot \frac{\partial \hat{y}_t^{(j)}}{\partial \beta_j} = g_j\)，\(\frac{\partial \beta_j}{\partial b_h} = w_{hj}\)，\(b_h = f(\alpha_h - \gamma_h)\)，\(\alpha_h = \sum_{i=1}^{d} v_{ih}x_t^{(i)}\):

\[\frac{\partial E_t}{\partial v_{ih}} = b_h(1 - b_h)x_t^{(i)}\sum_{j=1}^{c}g_j w_{hj} = e_hx_t^{(i)} \]

---

由上述推导，得到网络参数更新公式：

---

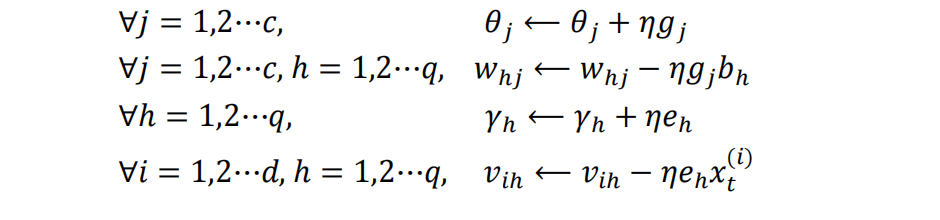
2.5 BP 算法缺点

随着网络层数增多，靠近输入端的神经元的梯度项逐渐减小，直至 消失(趋于0)，这种现象称为 “梯度消失”，
这使得无法对网络参数实现有效调节。因此，BP网络适用于浅层网络的学习，不适合深层次网络的学习。

---