[模式识别复习笔记] 第8章 决策树

1. 决策树

1.1 决策树简介

决策树（Decision Tree）是一种以 树形数据结构 来展示决策规则和分类结果的模型。每一条从根结点（对最终分类结果贡献最大的属性）到叶子结点（最终分类结果）的路径都代表一条决策的规则。

---

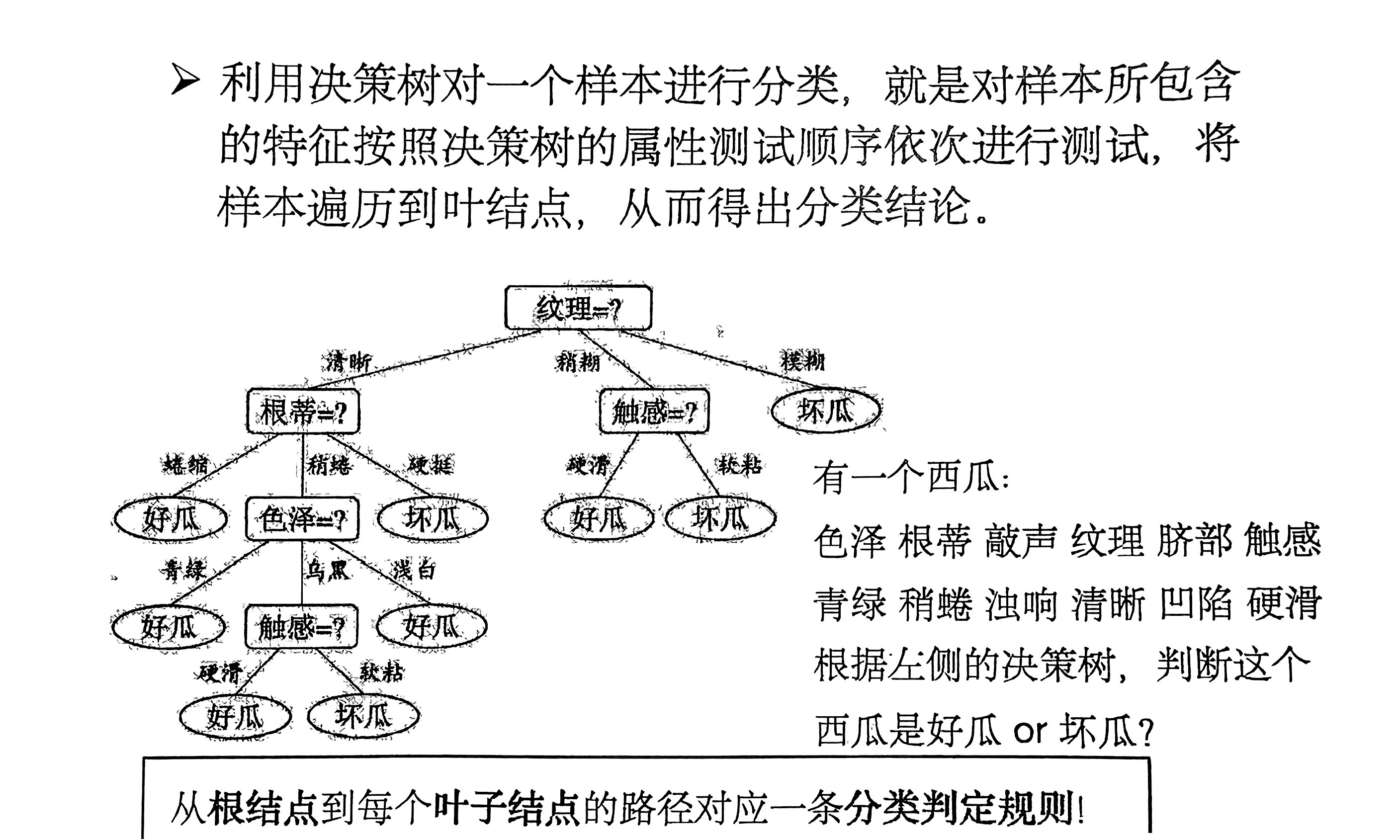
1.2 决策树的构建过程

1. 首先生成一个 根节点，其 包含所有的样本。

2. 判断划分：

   • 若 当前节点中所有样本 都属于 同一类别 \(C\)。此时 无需再进行划分，此节点 标记为 \(C\) 类别的叶子节点。

   • 若 数据为空，此时 无法进行划分，此节点 标记为 \(D\) 中样本最多的类。

3. 选择当前条件下的 最优属性进行划分。

4. 经历上步骤划分后，生成新的节点。

   继续循环判断，不断生成新的分支节点，直到所有节点都跳出循环。

   最后生成一颗决策树。

---

2. 最优划分属性的选择

2.1 信息增益

2.1.1 基本概念

• 信息熵

  熵 用来衡量一个随机变量取值的不确定程度，设 \(X\) 是一个取有限个值（\(m\) 类）的离散随机变量，其概率分布为:

  \[P(X = x_i) = p_i, \ i = 1, \ldots, m \]

  则随机变量 \(X\) 的熵定义为：

  \[\text{Ent}(X) = -\sum_{i=1}^{m}p_i \log p_i \]

  当 \(p_i = 0\) 时，定义 \(0 \log 0 = 0\)。

  当 \(\log\) 以 \(2\) 为底，此时熵的单位为比特 \(\text{bit}\)；

  当 \(\log\) 以 \(e\) 为底，此时熵的单位为纳特 \(\text{nat}\)。

• 信息熵的性质

  熵只依赖于随机变量的分布。

  对于一个有 \(m\) 个取值的随机变量 \(X\)，可以证明：

  • 当 \(p_1 = p_2 = \cdots = p_m = \frac{1}{m}\) 时，也就是 所有概率相等 时，\(X\) 的熵取得最大值 \(\log m\)。

  • 当 \(p_i = 1, \ \forall i \not = j, \ p_j = 0\) 时，\(X\) 的熵取得最小值 \(0\)。

  熵越大，表明随机变量 \(X\) 的取值的 不确定性越大。

• 条件熵 \(\text{Ent}(X|Y)\)

  衡量随机变量 \(Y\) 的取值已知的条件下，随机变量 \(X\) 取值的不确定性：

  \[\text{Ent}(X|Y) = \sum_{i=1}^{m}P(Y = y_i)\text{Ent}(X|Y=y_i) \]

• 信息增益 \(gain(X, Y)\)

  表示在得知 \(Y\) 后，随机变量 \(X\) 不确定性减少的程度，也是 确定性增加的程度:

  \[gain(X, Y) = \text{Ent}(X) - \text{Ent}(X|Y) \]

---

2.1.2 基于信息增益学习决策树

在决策树中，将样本类别看作是一个随机变量。对于一个 \(c\) 类的分类问题，类别变量的分布为：

\[P(\text{class} = i) = \frac{训练集 D 中第 i 类样本的数目}{训练集 D 中 所有样本的总数}, \ \ i = 1, \ldots, c \]

记 \(p_i = P(\text{class} = i)\)，则类别变量的熵为：

\[\text{Ent}(\text{class}) = - \sum_{i=1}^{c}p_i \log p_i \]

将类别变量的熵称为 训练集 \(D\) 的熵，记为 \(\text{Ent}(D)\)。

假设选取了属性 \(a\) 对样本进行划分，属性 \(a\) 有 \(k\) 个不同的取值 \(\{ a^{(1)}, a^{(2)}, \cdots, a^{(k)} \}\)，样本集 \(D\) 对应划分成 \(k\) 个子集 \(D_1, D_2, \ldots, D_k\)。

用 \(|D_i|\) 表示属性 \(a\) 取值为 \(a_i\) 的对应的划分出来的 \(D_i\) 的大小。

选择 \(a\) 属性对样本集 \(D\) 进行划分产生的 信息增益：

\[gain(D, a) = \text{Ent}(D) - \text{Ent}(D | a) \]

\[\text{Ent}(D | a) = \sum_{i=1}^{k}\frac{|D_i|}{|D|}\text{Ent}(D_i) \]

而选择的 最优划分属性 是信息增益最大的属性（增加确定性最多）：

\[a^{*} = \text{argmax}_{a\in A}gain(D, a) \]

例题 1

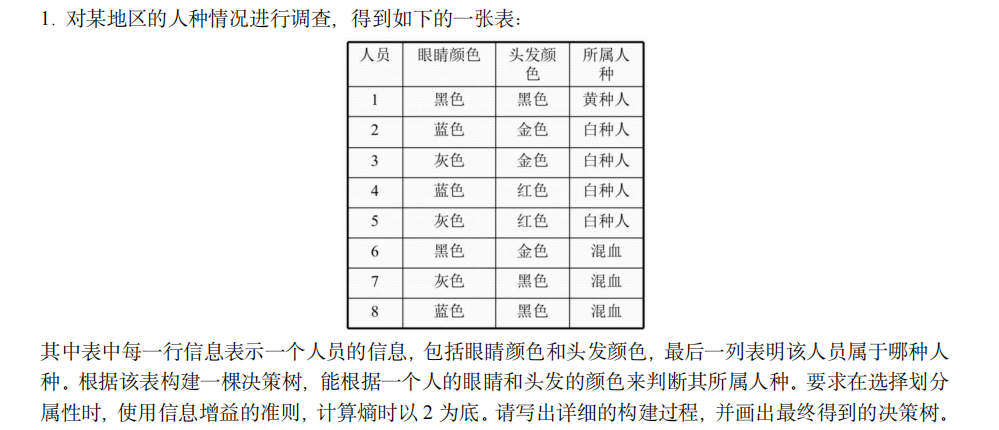
解：

---

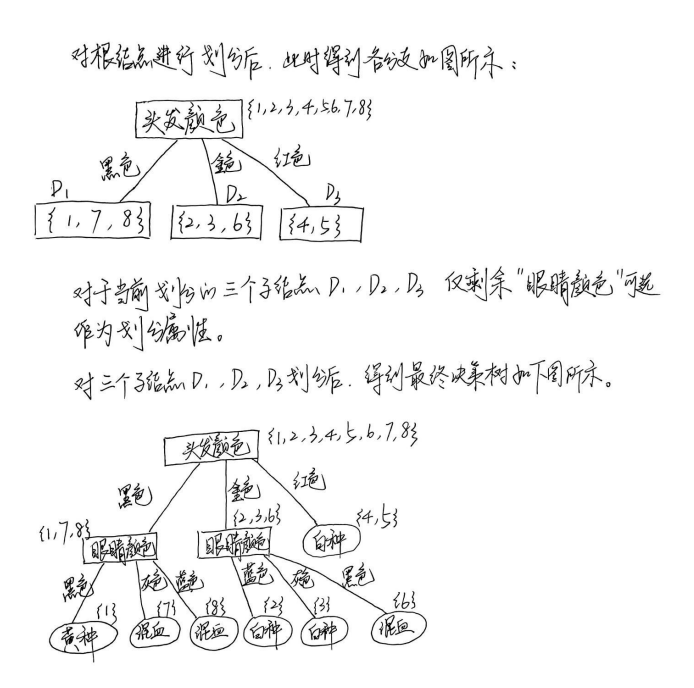
例题 2

设 \(X\) 是一个离散型随机变量，其概率分布为：

\[P(X = x_i) = p_i , i = 1,2, \cdots, m \]

求 \(X\) 的 熵的最大值，其中熵以 纳特 为单位。

---

2.2 基尼指数

2.2.1 基本概念

• 基尼值

  给定一个样本集 \(D\)，记 \(p_i\) 是 \(D\) 中第 \(i\) 类样本所占比例，\(i = 1, \ldots, c\)。从 \(D\) 中 随机抽取两个样本，则 两个样本类别不同的概率 为：

  \[\sum_{i=1}^{c}p_i(1 - p_i) = 1 - \sum_{i=1}^{c}p_i^2 \]

  样本集 \(D\) 的 基尼值 定义为：

  \[Gini(D) = 1 - \sum_{i=1}^{c}p_i^2 \]

  \(Gini(D)\) 反映了样本集 \(D\) 的不纯度。\(Gini(D)\) 越大，样本集 \(D\) 的不纯度越大（纯度越低）。

• 基尼指数

  属性 \(a\) 关于样本集 \(D\) 的 基尼指数 定义为：

  \[Gini\_index(D, a) = \sum_{i=1}^{k}\frac{|D_i|}{|D|}Gini(D_i) \]

---

2.2.2 基于基尼指数学习决策树

在候选属性集合 \(A\) 中，选择使得 基尼指数最小 的属性作为最优划分属性：

\[a^{*} = \text{argmin}_{a\in A}Gini\_index(D, a) \]

例题 1

将 2.1.2 中的例题 1 改为采用基尼指数判断最优划分属性。写出决策树的构建过程。

解：