[模式识别复习笔记] 第5章 贝叶斯分类器
1. 贝叶斯分类器
1.1 贝叶斯公式
假设有一个试验的样本空间为 \(S\)，记 \(B_1, B_2, \ldots, B_c\) 为 \(S\) 的一个划分，\(A\) 为试验的条件，且 \(P(A) \not = 0\)，则：
\(P(B_i)\) 先验概率：\(B_i\) 发生的概率，与 \(A\) 的发生无关。
\(P(A|B_i)\) 条件概率：\(B_i\) 发生的情况下，\(A\) 发生的概率。
\(P(B_i|A)\) 后验概率：\(A\) 发生的情况下，\(B_i\) 发生的概率，该概率根据 先验概率 和 条件概率 计算后得到。
对于一个包含 \(c\) 个类别 \(\{ w_1, \ldots, w_c \}\) 的一个分类问题，记 \(P(w_i|\bm{x})\) 表示观察特征向量取值为 \(\bm{x}\) 时，\(\bm{x}\) 属于 \(w_i\) 的概率，也即 后验概率。
-
若特征向量 \(\bm{x}\) 取值每一维度 连续，则贝叶斯公式为：
\[P(w_i|\bm{x}) = \frac{P(w_i)p(\bm{x}|w_i)}{p(\bm{x})} = \frac{P(w_i)p(\bm{x}|w_i)}{\sum_{j=1}^{c}P(w_j)p(\bm{x}|w_j)} \]其中 \(p(\bm{x})\) 称为特征向量取值为 \(\bm{x}\) 的概率密度；\(P(w_i)\) 为 \(w_i\) 类实例出现的概率，即 先验概率；\(p(\bm{x}|w_i)\) 为 \(w_i\) 类中特征向量取值为 \(\bm{x}\) 的概率密度，称为 类条件概率密度。
-
若特征向量 \(\bm{x}\) 取值每一维度 离散，则贝叶斯公式为：
\[P(w_i|\bm{x}) = \frac{P(w_i)P(\bm{x}|w_i)}{P(\bm{x})} = \frac{P(w_i)p(\bm{x}|w_i)}{\sum_{j=1}^{c}P(w_j)P(\bm{x}|w_j)} \]
1.2 贝叶斯分类
贝叶斯的分类规则 为将 \(\bm{x}\) 分到 后验概率 最大 的对应的类别中。
假设把 \(\bm{x}\) 分到 \(w_{i^{*}}\) 类中：
等价于:
先验概率时分类的基础，后验概率在获取更多信息后，对先验概率进行修正而得到。
1.3 贝叶斯分类的错误率
记 \(P(error|\bm{x})\) 为观察到实例的特征向量取值为 \(\bm{x}\) 时，贝叶斯分类的错误率。则：
故贝叶斯分类的总错误率为 \(P(error)\):
贝叶斯分类 通过 最小化 \(P(error|\bm{x})\) 来最小化总体的错误率。
1.4 最小化风险的贝叶斯分类
假设将 \(\bm{x}\) 分为 \(w_i\) 类，这一决策记为 \(\alpha_i\)。
损失 \(\lambda(\alpha_i|w_j)\) 定义为真实状态类别为 \(w_j\) 时，采取决策 \(\alpha_i\) 所导致的损失。通常是由一个函数设定。
条件风险 \(R(\alpha_i | \bm{x})\) 表示观察到实例对应的特征向量取值为 \(\bm{x}\) 时，将 \(\bm{x}\) 分为 \(w_i\) 类（采取决策 \(\alpha_i\)） 所产生的期望损失。有如下表达式：
PS；一般情况下，\(\lambda(\alpha_i|w_i) = 0\)。
由此得到 最小化风险的贝叶斯分类规则，即将 \(\bm{x}\) 分为 \(w_i\) 类（采取决策 \(\alpha_i\)）:
假设损失函数 \(\lambda\) 定义为：
也就是 \(\text{0-1}\) 损失函数。
带入条件风险计算公式得：
可以发现 \(1 - P(w_i|\bm{x})\) 就等价于 \(\bm{x}\) 被分为 \(w_i\) 时，贝叶斯分类的错误率。因此，当 采用 \(\text{0-1}\) 损失时，最小化风险就等价于最小化错误率（和前面找到最大后验概率的贝叶斯是等价的）：
2. 正态分布下的贝叶斯分类器
2.1 正态分布的概率密度函数
-
单变量 的正态分布
\(x \in \mathbb{R}, x \sim \mathcal{N}(\mu, \sigma^2)\)，有：
\[p(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x - \mu)^2}{2\sigma^2}} \] -
多变量 的正态分布
\(\bm{\bm{x}} \in \mathbb{R}^d, \bm{x} \sim \mathcal{N}(\mu, \Sigma)\)，有：
\[p(\bm{x}) = \frac{1}{(2\pi)^{\frac{d}{2}}|\Sigma|^{\frac{1}{2}}}e^{-\frac{1}{2}(\bm{x} - \bm{\mu})^{\text{T}}\Sigma^{-1}(\bm{x} - \bm{\mu})} \]\(\bm{x}\) 为 \(d\) 维向量，\(\bm{\mu}\) 为 \(d\) 维的均值向量。
\(\Sigma\) 为 \(d\times d\) 的协方差矩阵，\(\Sigma_{ij} = cov(x^{(i)}, x^{(j)})\)。\(|\Sigma|\) 和 \(\Sigma^{-1}\) 为 \(\Sigma\) 的行列式和逆矩阵。
2.2 判别函数表示贝叶斯分类规则
对于一个有 \(c\) 个类别的分类问题，定义 \(c\) 个判别函数：
或者
分类规则：将 \(\bm{x}\) 分到最大的 \(g_i(\bm{x})\) 对应的类别，也就是 \(w_i\) 类中。
2.3 正态分布下的贝叶斯分类
取判别函数 \(g_i(\bm{x}) = \ln p(\bm{x}|w_i) + \ln P(w_i), \ i = 1, \ldots, c\)。
假设 \(w_i\) 类实例对应的特征向量服从 \(\mathcal{N}(\mu, \Sigma)\) 正态分布：
带入到判别函数 \(g_i(\bm{x})\):
其中 \(\frac{d}{2}\ln 2\pi\) 不影响比较结果，可忽略。
故判别函数简化为：
每类正态分布的 协方差矩阵均相等，各类中 各个维度的特征相互独立且方差相同，每类样本 先验概率 相等，即 \(\Sigma_i = \sigma^2 I, \ i = 1, \ldots, c\)（其中 \(I\) 为单位阵）
可知 \(P(w_i) = \frac{1}{c}, \ i = 1, \ldots, c\)，带入 \(g_i(\bm{x})\) 可得：
其中 \(- \ln c - d \ln \sigma\) 不影响结果。
故判别函数简化为：
根据前面提到的分类规则（将 \(\bm{x}\) 分到最大的 \(g_i(\bm{x})\) 对应的类别，也就是 \(w_i\) 类中。），规则本质转化为：
也就是说，\(\bm{x}\) 距离哪一类的均值向量最近，就分为哪一类。（最近邻，欧氏距离度量）
2.4 分类决策面函数
第 \(i\) 类和 第 \(j\) 类之间的分类决策超平面方程满足：
将 \(g_i(\bm{x})\) 和 \(g_j(\bm{x})\) 带入，可以整理成：
得到:
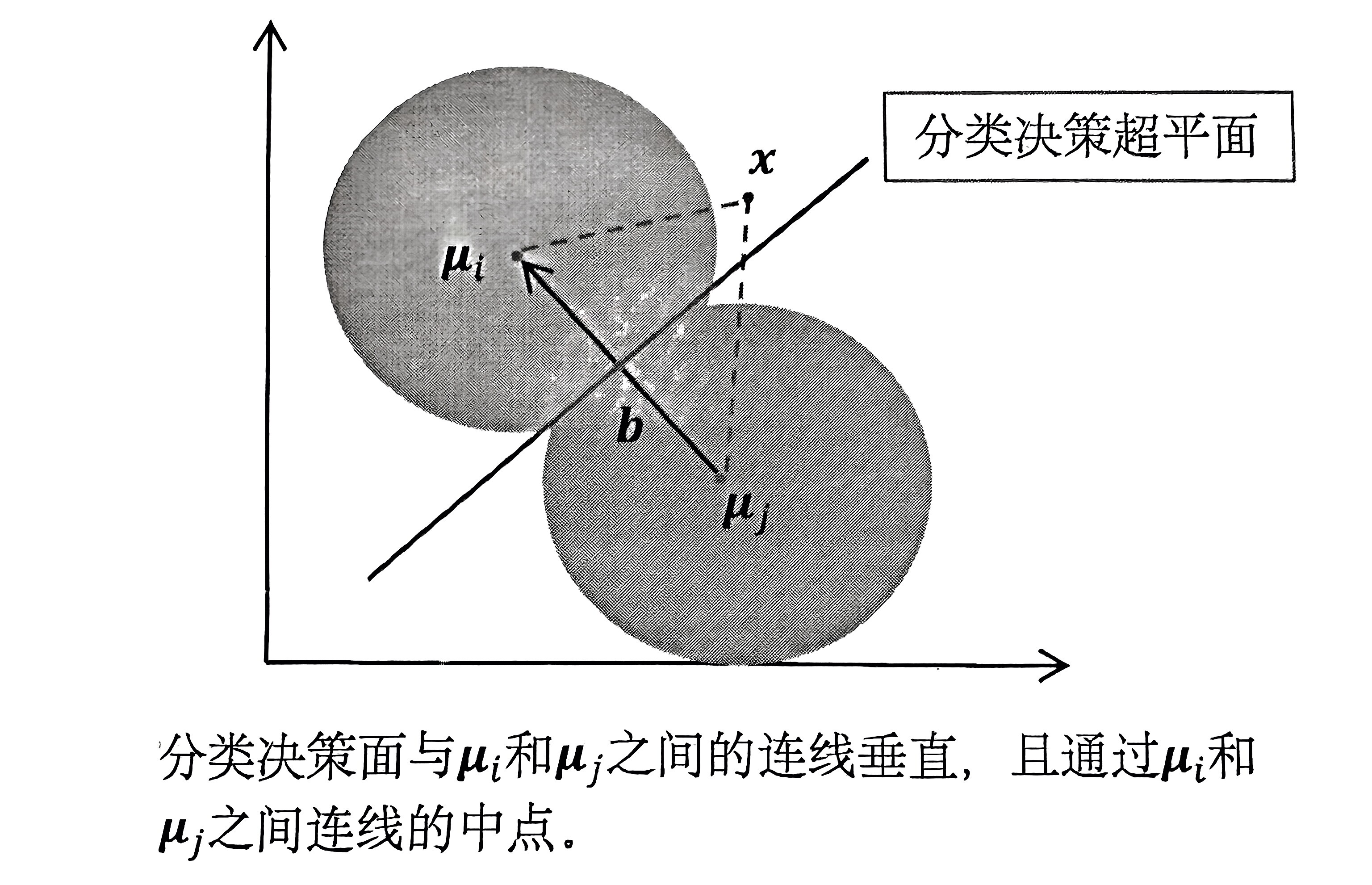
可以发现，贝叶斯分类器转换成了一个 线性分类器
3. 贝叶斯分类器的训练
3.1 参数估计
-
先验概率 \(P(w_j)\) 的估计
-
当训练样本足够多时，且每个样本随机抽取，可以直接用 训练集中 \(w_j\) 样本所占比例来估计 \(P(w_j)\)：
\[\hat P(w_j) = \frac{n_j}{N} \]其中 \(n_j\) 为训练集中 \(w_j\) 类样本的个数，\(N\) 为训练集中样本总数。
-
如果训练样本不随机，也可以假设各类样本的出现时等概率的：
\[P(w_j) = \frac{1}{c} \]其中 \(c\) 为类别的总数。
-
-
类条件概率密度 \(p(x|w_j)\) 的估计
-
非参数化估计方法
直接对概率 \(p(x|w_j)\) 函数本身进行估计，不必假设其服从某一分布。
-
参数化估计方法
先假定 \(p(\bm{x}|w_j)\) 具有特定的分布形式（如正态分布、二项分布），但是 分布参数未知，需要用 训练集来更新参数。
-
最大似然估计：将估计参数 \(\bm{\theta}\) 看作固定的量，但是取值未知。然后找到一组参数的值，最大化训练集所有样本出现的联合概率密度 \(p(D^{j}|\bm{\theta})\)。（每一类样本集 \(D^j\) 有对应不同的参数 \(\theta^{j}\)）
-
贝叶斯估计：：将估计参数 \(\bm{\theta}\) 看作随机的量，具有已知的先验概率密度函数 \(p(\bm{\theta})\)。观察到 \(w_j\) 类样本集 \(D^j\)，将参数 \(\bm{\theta}\) 的先验概率密度函数 \(p(\bm{\theta})\) 转换为 后验概率密度函数 \(p(\bm{\theta}| D^j)\)。
-
-
3.2 最大似然估计法
最大似然估计的假设：
-
\(D^{j}\) 中包含 \(n\) 个实例样本，即 \(D^{j} = \{ \bm{x}_1, \bm{x}_2, ... \bm{x}_n \}\)
-
\(p(\bm{x}|\bm{\theta^{j}})\) 记为 \(w_j\) 类的条件概率密度函数。
\(D^j\) 中每个 \(x_i\) 都是根据密度函数 \(p(\bm{x}|\bm{\theta^{j}})\) 的分布独立采样得到的。（独立同分布）
样本集 \(D^j\) 中所有样本的联合概率密度可以表示为：
称之为 似然函数 \(L(\bm{\theta}^j)\)，即：
最大似然估计就是 找到最优的 \(\bm{\theta}^j\) 的取值，使得似然函数 \(L(\bm{\theta}^j)\) 取得最大值。一般通过令导数为 0 求极值点来求解。
上述似然函数为 乘积形式，因此转换为对数更好求解：
令对数似然函数关于 \(\bm{\theta}^j\) 的导数为 \(0\) （向量）并求出极值点，从而得到 \(\bm{\theta}^j\) 的估计值：
例题 1
假设 \(D^j\) 中样本根据 正态分布 \(\mathcal{N}(\bm{\mu}, \bm{\Sigma})\) 得到，\(\bm{\mu}, \bm{\Sigma}\) 未知，要求用 \(\text{MLE}\) （最大似然估计）对这些参数进行估计。
解：
-
似然函数：
\[\begin{split} L(\bm{\mu}, \bm{\Sigma}) &= \prod_{i=1}^{n}p(\bm{x}_i | \bm{\mu}, \bm{\Sigma}) \\\\ &= (\frac{1}{(2\pi)^{\frac{d}{2}}|\bm{\Sigma}|^{\frac{1}{2}}})^{n} e^{-\frac{1}{2} \sum_{i=1}^{n}(\bm{x}_i - \bm{\mu})^{\text{T}}\bm{\Sigma}^{-1}(\bm{x}_i - \bm{\mu})} \end{split} \] -
对数似然函数：
\[\ln L(\bm{\mu}, \bm{\Sigma}) = -\frac{dn}{2}\ln 2\pi - \frac{n}{2}\ln |\bm{\Sigma}| - \frac{1}{2}\sum_{i=1}^{n}(\bm{x}_i - \bm{\mu})^{\text{T}}\bm{\Sigma}^{-1}(\bm{x}_i - \bm{\mu}) \] -
分别对 \(\bm{\mu}, \bm{\Sigma}\) 求梯度：
\[\nabla_{\bm{\mu}} \ln L(\bm{\mu}, \bm{\Sigma}) = \sum_{i=1}^{n}\bm{\Sigma}^{-1}(\bm{x}_i - \bm{\mu}) = 0 \]\[\nabla_{\bm{\Sigma}} \ln L(\bm{\mu}, \bm{\Sigma}) = -\frac{n}{2}(\bm{\Sigma}^{-1})^{\text{T}} + \frac{1}{2}\sum_{i=1}^{n}\bm{\Sigma}^{-\text{T}}(\bm{x_i} - \bm{\mu})(\bm{x_i} - \bm{\mu})^{\text{T}}\bm{\Sigma}^{-\text{T}} = 0 \]
PS：常用求导公式如下：
求解上述方程可以得到最终的参数估计值：
例题 2
假设 \(D^j\) 中样本根据 伯努利分布 得到，即 \(p(x|\theta) = \theta^{x}(1 - \theta)^{1 - x}\) ，其中 \(x = {0, 1}\) ，\(0 \le \theta \le 1\)，要求用 \(\text{MLE}\) （最大似然估计）对 \(\theta\) 进行估计。
解：
-
似然函数：
\[\begin{split} L(\theta) &= \prod_{i=1}^{n}p(x_i|\theta) \\\\ &= \prod_{i=1}^{n}\theta^{x_i}(1 - \theta)^{1 - x_i} \\\\ &= \theta^{\sum_{i=1}^{n}x_i} (1 - \theta)^{\sum_{i=1}^{n}(1 - x_i)} \end{split} \] -
对数似然函数：
\[\ln L(\theta) = (\sum_{i=1}^{n}x_i)\ln \theta + (\sum_{i=1}^{n}(1 - x_i))\ln (1 - \theta) \] -
对 \(\theta\) 求梯度：
\[\nabla_{\theta}\ln L(\theta) = \frac{1}{\theta}\sum_{i=1}^{n}x_i - \frac{1}{1 - \theta}\sum_{i=1}^{n}(1 - x_i) = 0 \]整理可得：
\[\frac{1}{\theta}\sum_{i=1}^{n}x_i + \frac{1}{1 - \theta}\sum_{i=1}^{n}x_i = \frac{n}{1 - \theta} \]即：
\[\frac{1}{\theta (1 - \theta)} \sum_{i=1}^{n}x_i = \frac{n}{1 - \theta} \]
求解上述方程可以得到最终的参数估计值：
3.3 贝叶斯估计法
贝叶斯估计法的假设：
-
\(p(\bm{x}|\bm{\theta^{j}})\) 形式已知，参数 \(\bm{\theta}^j\) 未知，是一个随机量。具有已知的先验概率密度函数 \(p(\bm{\theta}^j)\)。
-
\(D^j\) 中每个 \(x_i\) 都是根据密度函数 \(p(\bm{x}|\bm{\theta^{j}})\) 的分布独立采样得到的。
样本集 \(D^j\) 中所有样本的联合概率密度可以表示为：
利用贝叶斯公式，计算观察到 \(D^j\) 后 \(\bm{\theta}^j\) 的 后验概率密度：
求得参数 \(\hat{\bm{\theta}^j}\):
例题 1
给定一个样本集 \(D = \{ x_1, x_2, \ldots, x_n \}\)，设 \(D\) 中的每个样本都是根据 一维的正态分布 \(\mathcal{N}(\mu, \sigma^2)\) 相互独立采样得到，参数 \(\mu\) 未知，\(\sigma^2\) 已知。参数 \(\mu\) 服从一个已知的先验概率分布 \(\mathcal{N}(\mu_0, \sigma_0^2)\)。
要求用贝叶斯估计法对参数 \(\mu\) 进行估计。
解：
由题意可知：
-
计算 \(p(D | \mu)\):
\[\begin{split} p(D | \mu) &= \prod_{i=1}^{n}p(x_i | \mu) \\\\ &= (\frac{1}{\sqrt{2\pi} \sigma})^{n} e^{-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(x_i - \mu)^2} \end{split} \] -
计算参数 \(\mu\) 的 后验概率密度 \(p(\mu | D)\):
\[\begin{split} p(\mu | D) & \propto p(\mu)p(D | \mu) \\\\ & \propto e^{-\frac{1}{2}[(\frac{n}{\sigma^2} + \frac{1}{\sigma^2_0})\mu^2 - 2(\frac{1}{\sigma^2}\sum_{i=1}^{n}x_i + \frac{\mu_0}{\sigma^2_0}\mu)]} \\\\ & \propto e^{-\frac{1}{2\sigma^2_n}(\mu - \mu_n)^2} \end{split} \]其中：
\[\mu_n = \frac{\sigma^2}{n\sigma^2_0 + \sigma^2}\mu_0 + \frac{n\sigma_0^2}{n\sigma^2_0 + \sigma^2}\mu_{\text{MLE}} \]\[\mu_{\text{MLE}} = \frac{1}{n}\sum_{i=1}^{n} x_i \]\[\frac{1}{\sigma_n^2} = \frac{n}{\sigma^2} + \frac{1}{\sigma_0^2} \] -
密度函数 \(p(\mu | D)\) 的分布的 数学期望 是 \(\mu_n\)，因此参数 \(\mu\) 的贝叶斯估计为：
\[\hat{\mu} = \mu_n \]
例题 2
给定一个训练集 \(D = \{ x_1, x_2, \ldots, x_n \}\)，样本是根据 伯努利 分布采样得到，即 \(p(x|\theta) = \theta^x (1 - \theta)^{1-x}\) ，其中参数 \(\theta\) 未知，\(x = \{ 0, 1 \}\)，\(0 \le \theta \le 1\)。
已知参数 \(\theta\) 服从一个已知的先验概率分布为 \(Beta\) 分布，即 \(\theta \sim Beta(\alpha, \beta)\):
PS：\(Beta\) 分布的期望为 \(\frac{\alpha}{\alpha + \beta}\) 。
要求用贝叶斯估计法对参数 \(\theta\) 进行估计。
解：
-
计算 \(p(D | \theta)\):
\[\begin{split} p(D|\theta) &= \prod_{i=1}^{n}p(x_i|\theta) \\\\ &= \prod_{i=1}^{n}\theta^{x_i}(1 - \theta)^{1 - x_i} \\\\ &= \theta^{\sum_{i=1}^{n}x_i} (1 - \theta)^{\sum_{i=1}^{n}(1 - x_i)} \end{split} \] -
计算参数的 后验概率密度 \(p(\theta | D)\):
\[\begin{split} p(\theta | D) &= \frac{p(\theta)p(D | \theta)}{p(D)} \\\\ & \propto \theta^{\alpha + \sum_{i=1}^n x_i - 1}(1 - \theta)^{\beta + n - \sum_{i=1}^{n}x_i - 1} \end{split} \]可以看出 \(p(\theta | D)\) 服从一个 \(Beta(\alpha + \sum_{i=1}^{n}x_i, \beta + n - \sum_{i=1}^{n}x_i)\) 的分布。
-
由密度函数 \(p(\theta | D)\) 的分布的 数学期望 ，得到参数 \(\theta\) 的贝叶斯估计为：
\[\begin{split} \hat{\theta} &= \frac{\alpha + \sum_{i=1}^{n}x_i}{\alpha + \beta + n} \\\\ &= \frac{\alpha + \beta}{\alpha + \beta + n}\cdot \frac{\alpha}{\alpha + \beta} + \frac{n}{\alpha + \beta + n}\theta_{\text{MLE}} \end{split} \]其中 \(\theta_{\text{MLE}} = \frac{1}{n}\sum_{i=1}^n x_i\) 。
一切都是命运石之门的选择，本文章来源于博客园，作者：MarisaMagic，出处：https://www.cnblogs.com/MarisaMagic/p/18259679，未经允许严禁转载
