[NLP复习笔记] 神经网络及BP算法
1. 神经网络
1.1 神经元
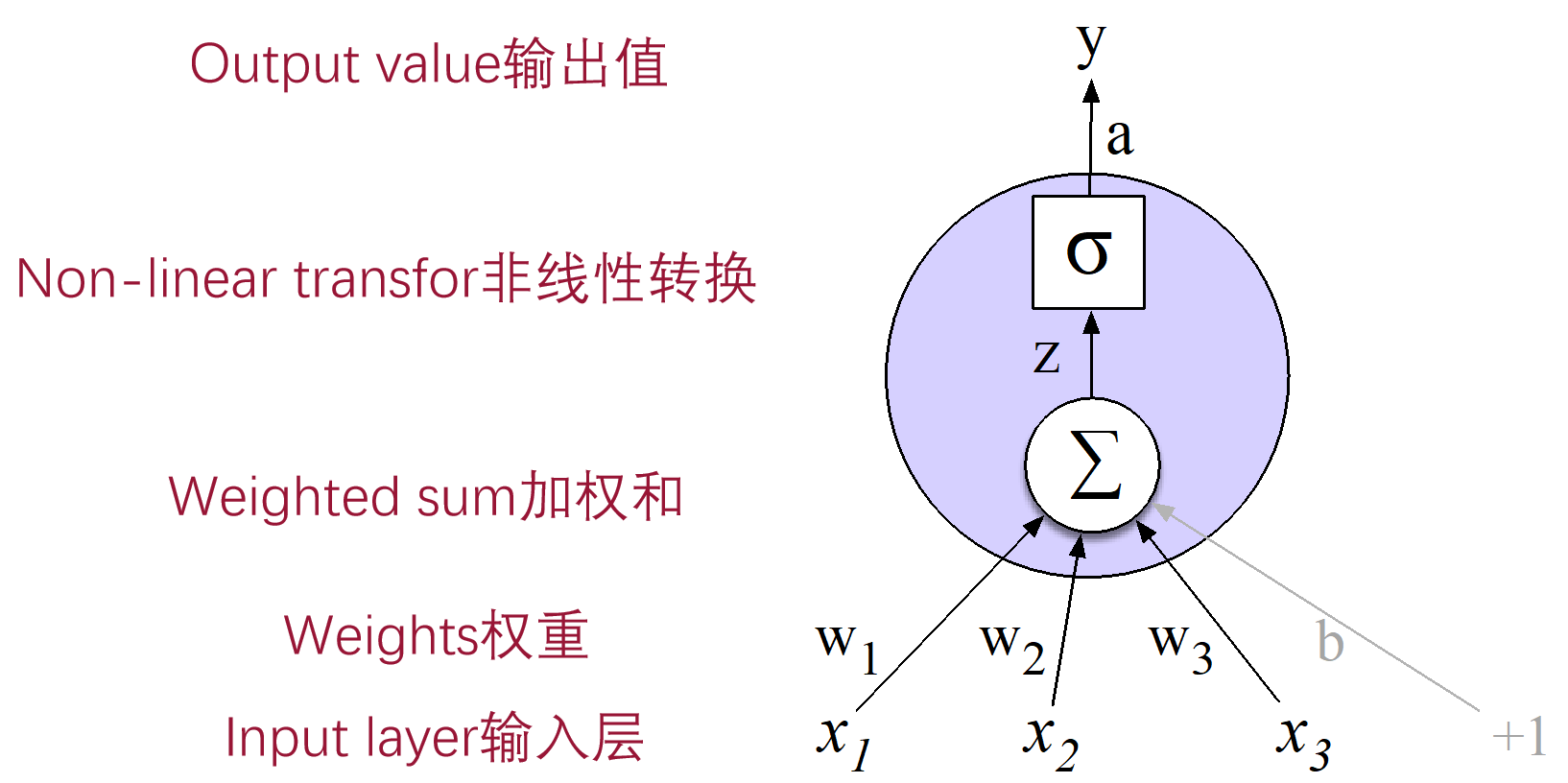
神经元(Neuron)或节点(Node) 是神经网络的基本单元。下图是一个简单的神经元示意图,\(x\) 表示 输入(\(\text{Input}\)), \(x_i\) 表示来自于前面第 \(i\) 个 神经元(\(\text{Neuron}\))的输入,通常会增加一个虚拟的 \(x_0 = 1\) 用于对应连接当前神经元的 权重 \(w\) 中的 偏置量(\(\text{bias}\))。
在进行数据的加权和偏置处理,以及通过 激活函数 \(\sigma\) 后,得到 隐藏输出(\(\text{Hidden}\)),在图中就是 \(a\)。这是神经网络进行特征学习的所在。
最后生成一个值/向量 \(y\) 作为当前这个神经元的输出(\(\text{Output}\))。
1.2 神经网络
通常情况下,神经网络有三种类型的层,每个层都由若干个神经元组成:
-
输入层(\(\text{Input Layer}\)):这是数据进入神经网络的地方,不进行任何计算。
-
隐藏层(\(\text{Hidden Layers}\)):介于输入层和输出层之间的层,可以有一个或多个。隐藏层进行数据的加权和偏置处理,以及激活函数的应用。
-
输出层(\(\text{Output Layer}\)):生成最终的输出,如分类预测或回归值。
在输入层到隐藏层、隐藏层到输出层之间,往往都会有 权重矩阵,权重决定了输入对于输出的贡献大小,是神经网络中的可学习参数。
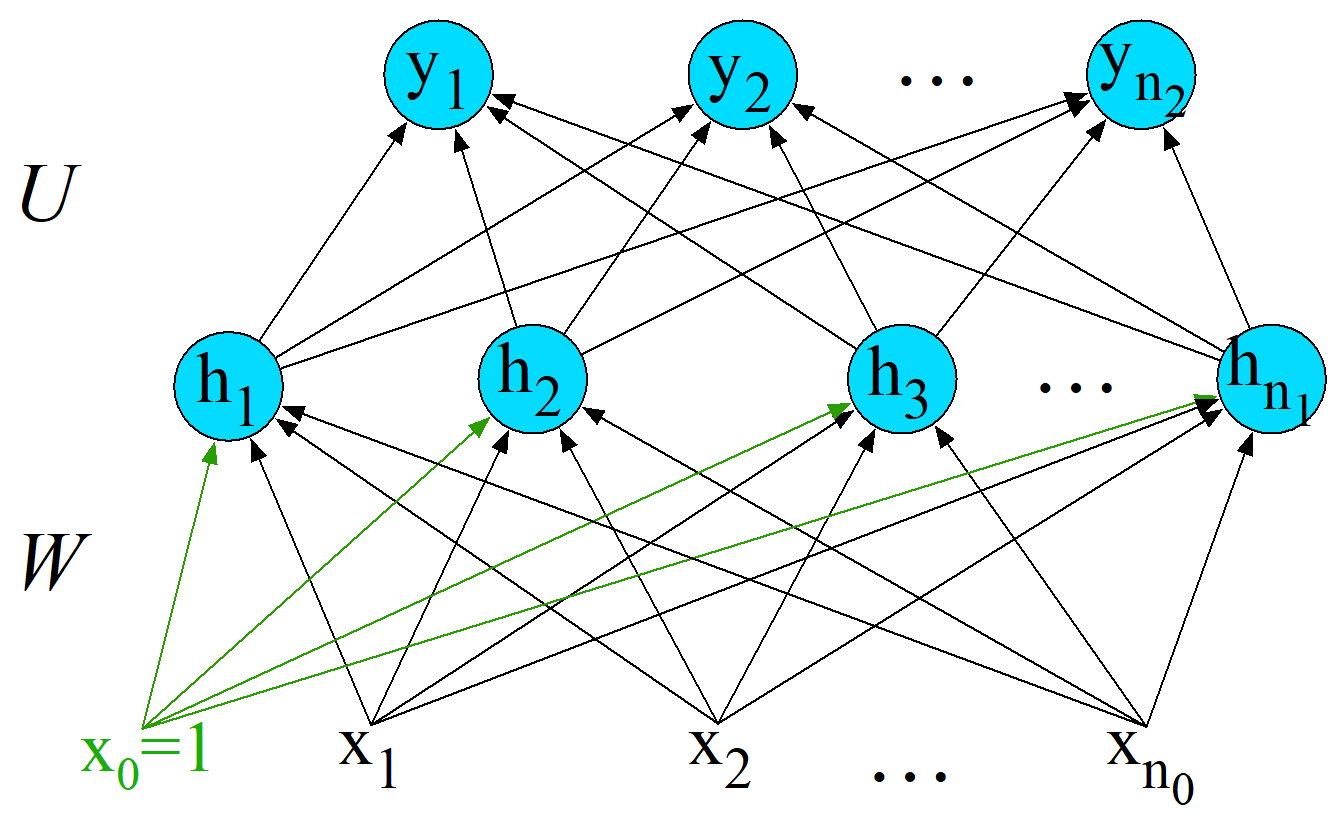
图中,\(x\) 表示输入层,\(W\) 为输入层到隐藏层的权重矩阵,\(h\) 表示隐藏层,\(U\) 为隐藏层到输出层的权值矩阵,\(y\) 为输出层。
假设输入层 \(x \in \mathbb{R}^{n \times 1}\),隐藏层 \(h \in \mathbb{R}^{d \times 1}\),显然权重矩阵 \(W \in \mathbb{R}^{d \times n}\),通过:
得到隐藏层向量,而这个 \(d\) 就是我们经过加权求和和偏置处理后,提取的特征的数量,相当于将 \(n\) 维度的空间映射到了 \(d\) 维度。隐藏层 \(h\) 往往会再通过一个激活函数 \(\sigma\),图中没有展示出来。
假设输出层 \(y \in \mathbb{R}^{m \times 1}\),那么隐藏层到输出层的权重矩阵 \(U \in \mathbb{R}^{m \times d}\),通过:
得到输出。不过,往往会再通过一个激活函数,此处一般采用 \(\text{softmax}\)。
2. 正向传播
正向传播 其实就是将一个样本 \(x\) 输入到神经网络,经过多层向前计算,最终得到输出 \(y\) 的过程。
最后,在正向传播结束后产生了预测输出 \(y\),然后与实际的标签或输出比较,计算 损失函数 \(L\)。
在神经网络中,损失函数 \(L\) 一般采用 交叉熵损失(\(\text{Cross-Entropy Loss}\)),常用于 分类任务。而本篇文章只讨论比较简单的二分类任务,所以用到的是 二分类交叉熵损失 (\(\text{Binary Cross-Entropy}\))
对于当前问题,我们有如下的损失函数 \(L\) :
3. 反向传播(BP算法)
3.1 BP算法简介
\(\text{BP}\) 算法,即 反向传播算法(\(\text{Backpropagation Algorithm}\)),是一种用于训练神经网络的常用方法。
在前面,我们定义了损失函数 \(L\),而反向传播的关键就是将输出误差以一种特定的方式传回网络,用于计算相对于每个权重的误差导数(梯度),而每个权重的梯度则反映了增加或减少这个权重,损失函数的值的变化。
使用这些梯度以及一个学习率参数来更新网络中的权重,我们通常采用 梯度下降法 。
经过反复迭代后,最小化损失函数,得到最优参数(权重)。
但是,我们无法直接得到导数 \(\frac{\partial L}{\partial w}\),此时就需要向前计算,采用 链式法则 来计算导数:

3.2 典型示例
我们用一个比较简单的示例来理解 \(\text{BP}\) 算法。如下图所示,是一个神经网络(虽然看起来很简陋),经过正向传播后计算出了每个神经元的值以及最后的损失函数值:
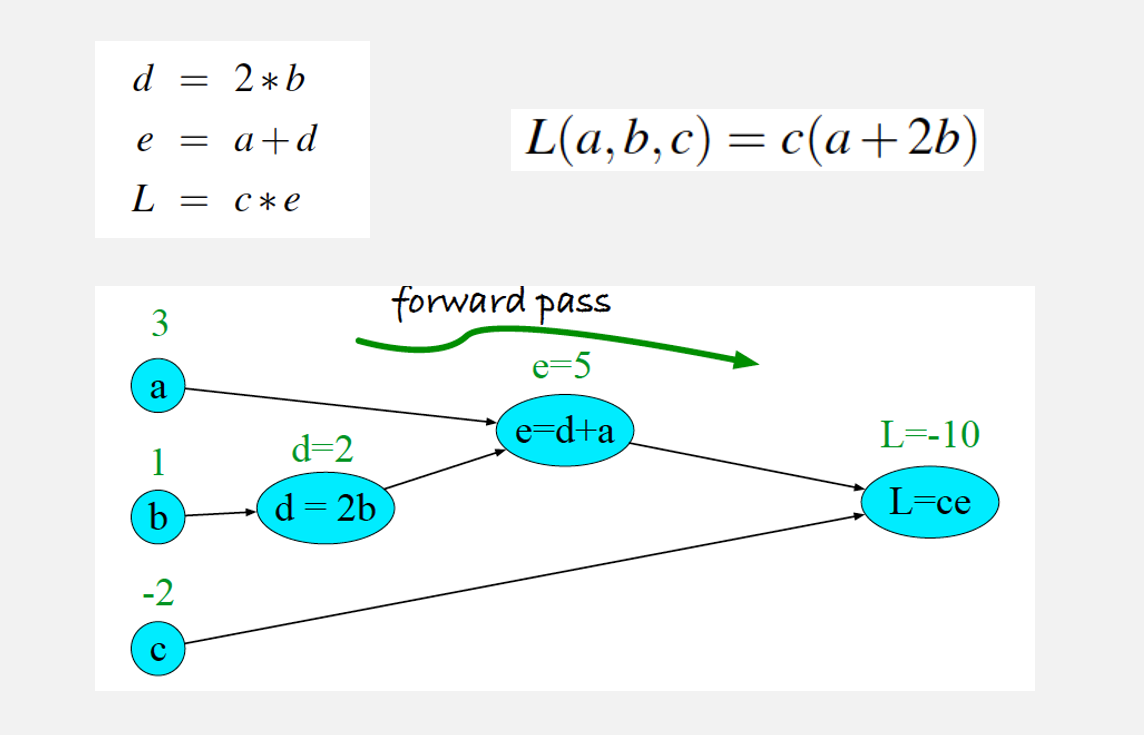
然后,我们从损失函数开始需要进行反向传播。因此,我们需要损失函数中每个权重对应的导数。
由链式求导法则:
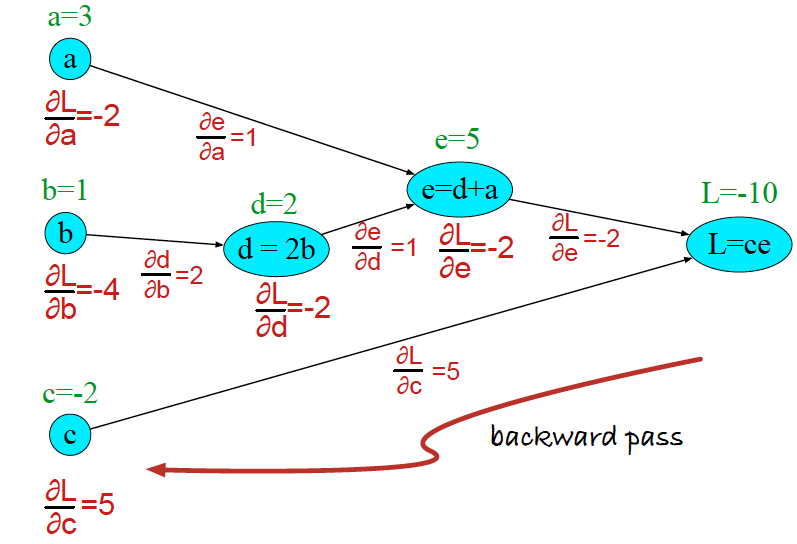
然而实际上的问题不止这么简单,对于一个分类问题,损失函数往往采用 交叉熵损失,且往往涉及激活函数 \(\text{sigmoid}\) 的求导、\(\text{ReLU}\) 的求导。
下图就是一个简单的示例:
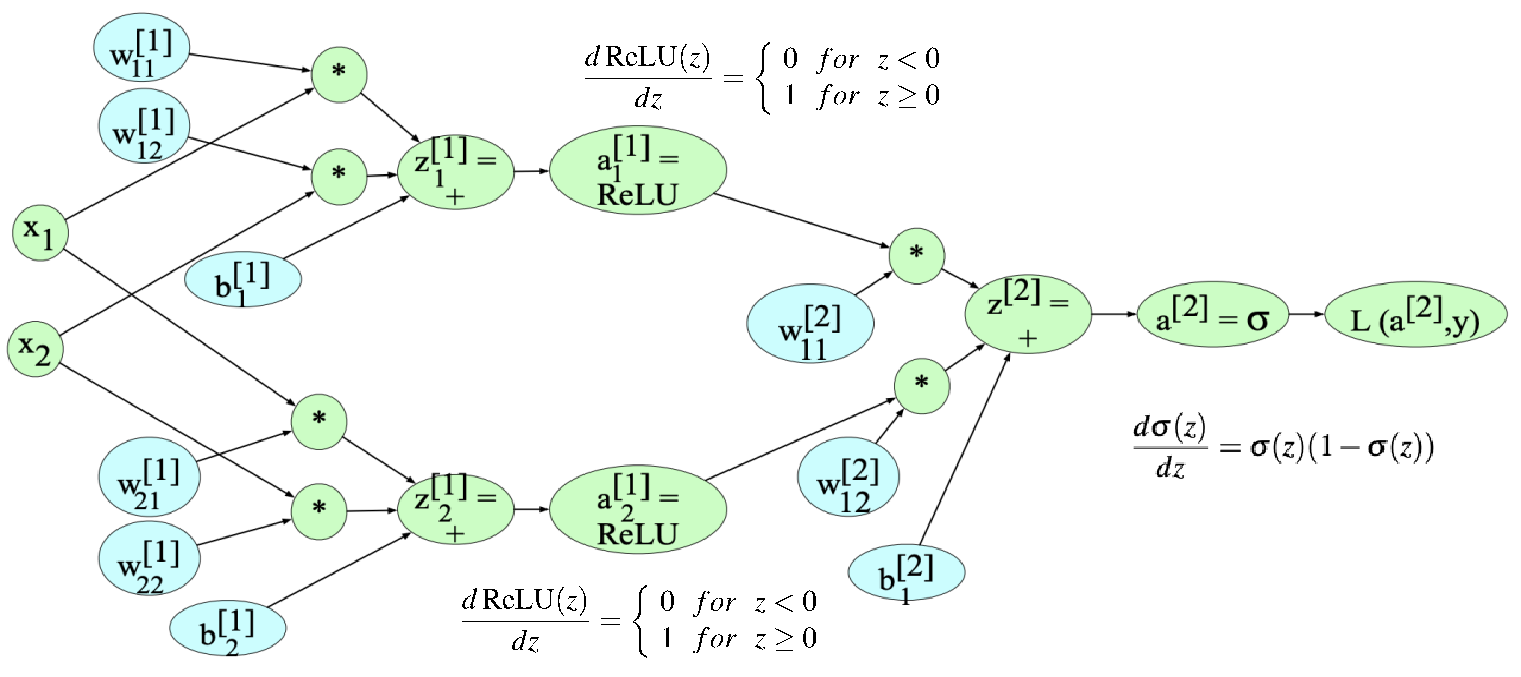
图中,输入层 \(x \in \mathbb{R}^{2 \times 1}\),输入层到隐藏层的权重矩阵 \(W^{[1]} \in \mathbb{R}^{2 \times 2}\),经过加权求和以及偏置后得到 \(z^{[1]} \in \mathbb{R}^{2 \times 1}\),经过 \(\text{ReLU}\) 函数激活得到隐藏层 \(a^{[1]} \in \mathbb{R}^{2 \times 1}\)。隐藏层到输出层的权重矩阵 \(W^{[2]} \in \mathbb{R}^{1 \times 2}\),经过加权求和与偏置得到 \(z^{[2]}\),然后经过 \(\text{sigmoid}\) 函数(也就是 \(\sigma\))得到最终的输出层 \(a^{[2]}\)。最后当前的计算损失函数值。
\(\text{sigmoid}\) 函数求导后为 \(\sigma(x)(1 - \sigma(x))\),具体证明可见 sigmoid函数求导-只要四步
类似于前面那个非常简陋的例子的过程,采用链式求导法则,可以得到如下导数公式的推导:
-
每一层的表达式
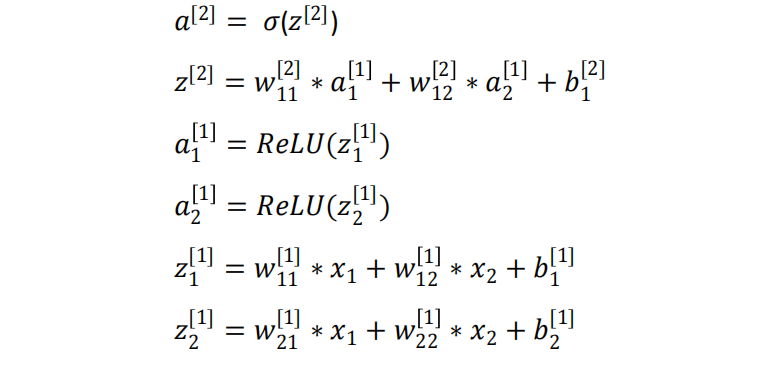
-
损失函数
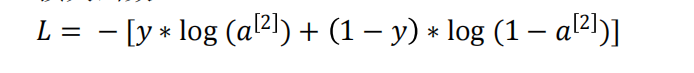
-
阶段求导
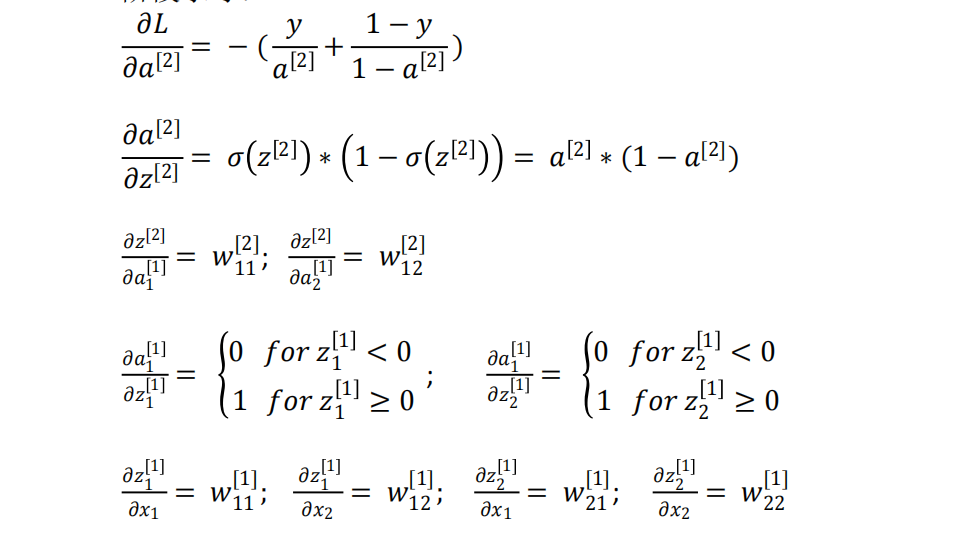
-
链式求导
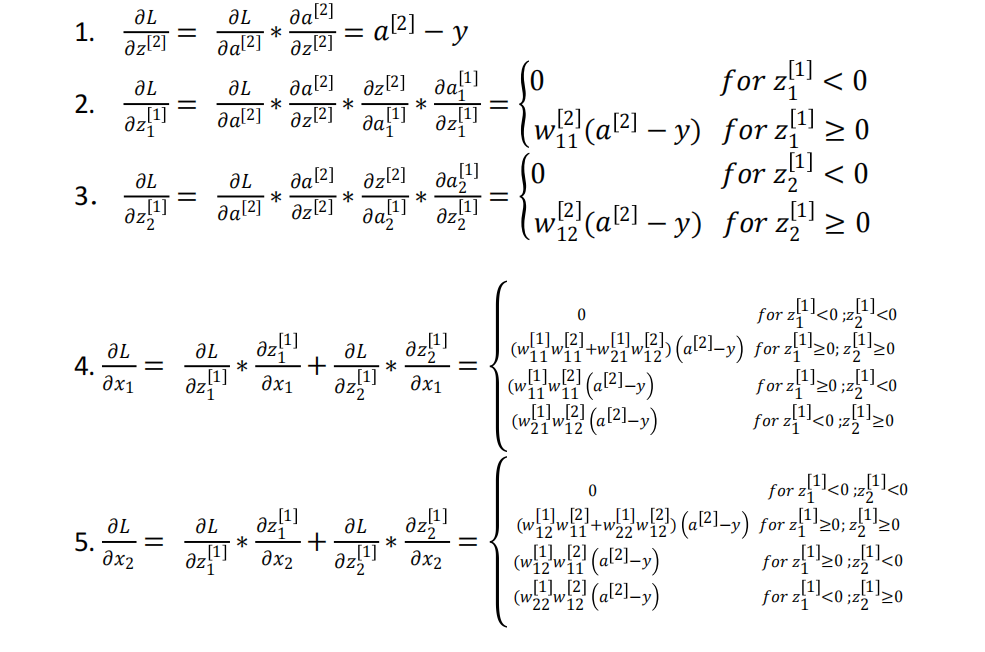
PS:这个是作业里的题目,直接贴图片了,还是很好理解的。
参考
《机器学习》周志华
一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MarisaMagic/p/17950907,未经允许严禁转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号