[最优化方法笔记] 非线性规划 拉格朗日乘子法

1. 拉格朗日乘子法

拉格朗日乘子法 是一种 将约束优化问题 转化 为 无约束优化问题 的方法。其核心思想就是通过 拉格朗日乘子 将 含有 \(n\) 个变量和 \(m\) 个约束条件的带约束优化问题转换为含有 \(n + m\) 个变量的无约束优化问题。

对于如下约束优化问题：

\[\begin{split} & \min f(x) \\ & \; \text{s.t.} \; g(x) = 0 \end{split} \]

其中 \(x \in \mathbb{R}^n\)

显然，约束 \(g(x) = 0\) 限制了解的空间，所以我们引入 拉格朗日乘子 \(\lambda\)，得到 拉格朗日函数：

\[L(x, \lambda) = f(x) + \lambda g(x) \]

拉格朗日函数 \(L\) 本身为一个无约束优化问题，原问题的 最优解 \(x^*\) 由如下方程组求解得到：

\[\begin{cases} \nabla_x L(x, \lambda) = 0 \\\\ g(x) = 0 \end{cases} \]

拉格朗日函数 \(L\) 对 \(x\) 的各个分量求偏导数，并且令偏导数为 \(0\)，求解上述方程组得到 可行解 \(x^*\)。

方程组所有条件是满足优化问题的必要条件，所以求出的解 不一定是最优解 ，但一定是可行的，且 最优解 \(x^*\) 一定包含在所有可行解中。

特别地，当 目标函数 \(f\) 是一个 凸函数 ，约束函数 也为 凸函数（其中如果是等式约束，要求其为仿射函数，仿射函数同时是凸函数和凹函数），方程组的解一定是 最优解。此时，就是一个 凸优化问题。

---

2. 等式约束优化问题

2.1 等式约束优化

假设如下等式约束优化问题：

\[\begin{split} & \min f(x, y) \\ & \;\text{s.t.} \; g(x, y) = c \end{split} \]

构造拉格朗日函数：

\[L(x, y, \lambda) = f(x, y) + \lambda(g(x, y) - c) \]

由此转化为无约束优化问题，有如下方程组：

\[\begin{cases} \nabla L(x, y, \lambda) = \nabla f(x, y) + \lambda \nabla g(x, y) = 0 \\ \lambda(g(x, y) - c) = 0 \end{cases} \]

我们可以形象化理解拉格朗日乘子法，如下图所示：

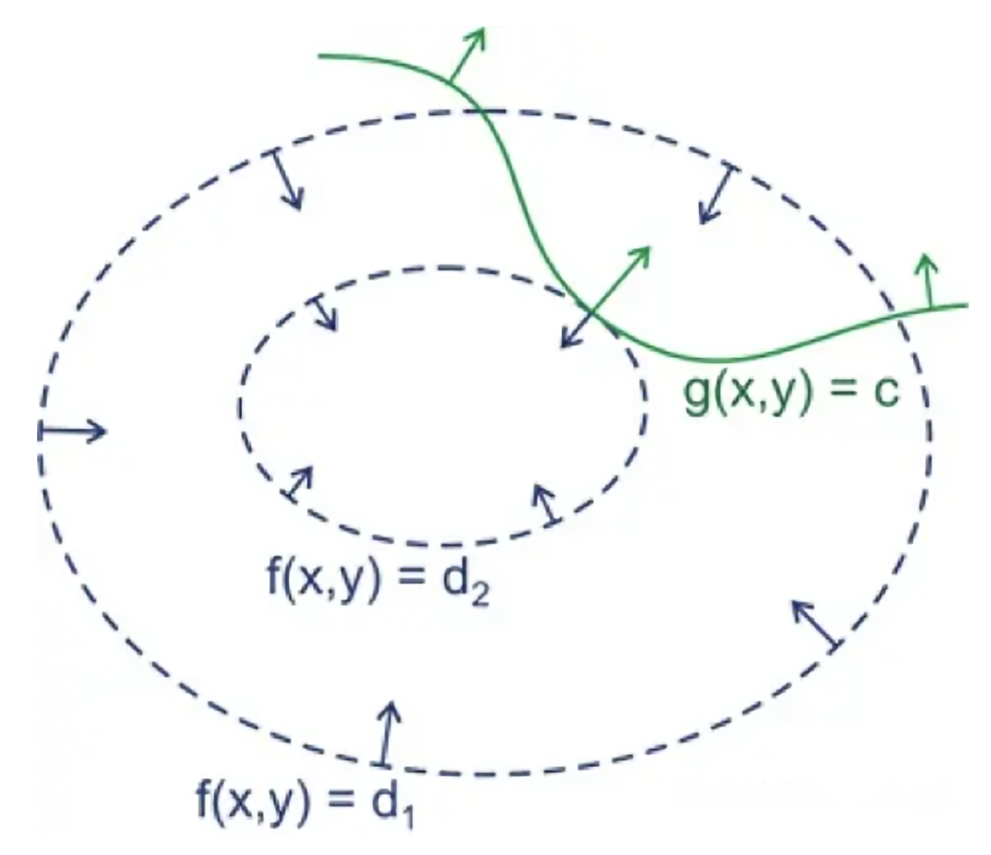
图中 绿色 的线表示 约束条件，蓝色 的虚线表示 目标函数 \(f\) 的等高线。

分为以下三种情况：

• 相离

• 相交

  两个函数相交的表明当前焦点是两个函数的解，但是相交得到的点不是最优值，因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小。

• 相切

  等高线与条件函数相切，只存在一个交点。

  目标函数 \(f\) 的梯度为 \(\nabla f(x, y)\) ，约束条件函数的梯度为 \(\nabla g(x, y)\)，因为 相切，所以两个函数的梯度有 \(\nabla f(x, y) = - \lambda \nabla g(x, y)\)

  显然，整理后得到：

  \[\nabla f(x, y) + \lambda \nabla g(x, y) = 0 \]

  恰好满足方程组中 \(\nabla L(x, y, \lambda) = 0\) 的条件。

2.2 等式约束二次规划

二次规划 是 非线性规划问题 中最简单的一类，我们这里用拉格朗日乘子法求解典型的等式约束二次规划来助于理解。

假设有二次规划问题如下：

\[\begin{split} & \min f(x) = \frac{1}{2} x^T Px + q^Tx \\ & \; \text{s.t.} \; Ax = b \end{split} \]

其中 \(x \in \mathbb{R}^n\) 为 \(n\) 元列向量，\(A \in \mathbb{R}^{m \times n}, \; b \in \mathbb{R}^m\) 表示了 \(m\) 个等式约束条件。

我们可以将所有等式约束写成：

\[a^T_i x = b_i \;, i = 1, 2, ... , m \]

引入拉格朗日乘子 \(\lambda_i, \; i = 1, 2, ... , m\), 那么我们可以得到拉格朗日函数：

\[L(x, \lambda) = \frac{1}{2} x^T Px + q^Tx + \sum_{i=1}^m \lambda_i (a_i^Tx - b_i) \]

有如下方程组：

\[\begin{cases} \nabla_x L(x, \lambda) = Px + q + \sum_{i=1}^m \lambda_i a_i = 0 \\ a_i^T x - b_i = 0, \; i = 1, 2, ... , m \end{cases} \]

求解得到可行解 \(x^*\) 以及满足条件的拉格朗日乘子 \(\lambda_i, \; i = 1, 2, ... , m\)。

---

3. 不等式约束优化问题

3.1 不等式约束优化

假设如下不等式约束优化问题：

\[\begin{split} & \min f(x, y) \\ & \;\text{s.t.} \; g(x, y) \le 0 \end{split} \]

此时可行区域变成了二维的。

为了形象理解，我们假定不等式约束条件 \(g(x, y) = x + y - 1\)，可行区域如图所示：

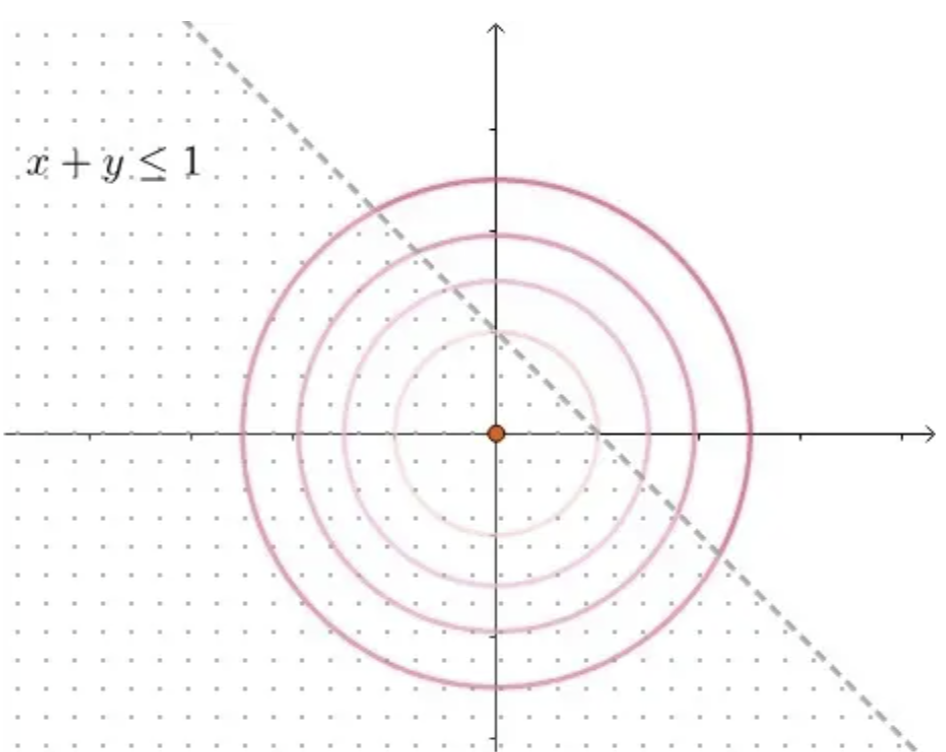
显然，最优解 \((x^*, y^*)\) 已经处于可行区域内。也就是说 \(x^*\) 在 \(g(x, y) < 0\) 的情况下取到。

我们假定不等式约束条件 \(g(x, y) = x + y + 2\)，可行区域如图所示：

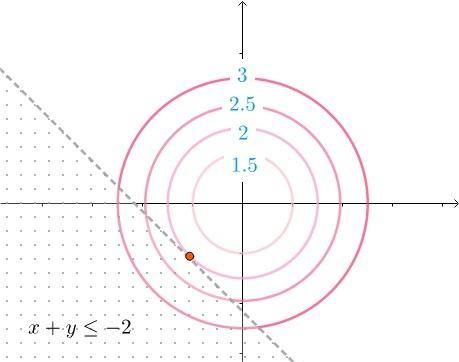
显然，最优解 \(x^*\) 处于可行区域且位于目标函数等高线和约束条件相切的位置。也就是说 \((x^*, y^*)\) 在 \(g(x, y) = 0\) 的情况下取到。

故可以不等式约束优化问题可以分为以下两种情况讨论：

• 最优解 \(x^*\) 位于 \(g(x) < 0\)，此时约束条件无作用，直接令 \(\nabla f(x) = 0\) 进行求解。此时 等价于拉格朗日乘子 \(\lambda = 0\)。

• 最优解 \(x^*\) 位于 \(g(x) = 0\)，相当于等式约束，在相切处取得最优解。显然，最优解 \(x^*\) 处的 \(\nabla f(x^*)\) 和 \(g(x^*)\) 反向，故一定存在常数 \(\lambda > 0\) 使得 \(\nabla f(x^*) = -\lambda \nabla g(x^*)\)。

综合上面两种情况，可以得出 拉个朗日乘子满足 \(\lambda g(x) = 0\)

所以，可以转换为如下几个约束条件：

\[\begin{cases} \nabla_x L(x, \lambda) = 0 \\ g(x) \le 0 \\ \lambda \ge 0 \\ \lambda g(x) = 0 \end{cases} \]

以上也被称为 \(\text{KKT}\) 条件。

3.2 混合情形

一般约束优化问题就是既有等式约束也有不等式约束，而且有多个。设有如下约束优化问题：

\[\begin{split} & \min f(x) \\ & \;\text{s.t.} \; h_i(x) = 0, \; i = 1, 2, ... , m_1 \\ & \;\;\; \quad g_j(x) \le 0, \; j = 1, 2, ... , m_2 \end{split} \]

其中 \(x \in \mathbb{R}^n\)

引入拉格朗日乘子 \(\lambda_i, \; i = 1, 2, ... , m_1\) 和 \(\mu_j \ge 0, \; j = 1, 2, ... , m_2\) 构造拉格朗日函数：

\[L(x, \lambda, \mu) = f(x) + \sum_{i=1}^{m_1} \lambda_i h_i(x) + \sum_{j=1}^{m_2} \mu_j g_j(x) \]

有如下方程组(\(\text{KKT}\) 条件)：

\[\begin{cases} \nabla_x L(x, \lambda, \mu) = 0 \\ h_i(x) = 0, \; i = 1, 2, ... , m_1 \\ g_j(x) \le 0, \; j = 1, 2, ... , m_2 \\ \mu_j \ge 0, \; j = 1, 2, ..., m_2 \\ \mu_j g_j(x) = 0, \; j = 1, 2, ... ,m_2 \end{cases} \]

---

参考

优化-拉格朗日乘子法

约束优化的拉格朗日乘子（KKT）

形象理解拉格朗日乘子法