[最优化方法笔记] 共轭梯度法

1. 共轭方向

设 \(A \in \mathbb{R}^{n \times n}\) 为 对称阵，\(p, q \in \mathbb{R}^{n \times 1}\) 为 n元列向量。如果:

\[p^T A q = 0 \]

则称 \(p\) 和 \(q\) 关于 \(A\) 共轭。

特别地，若 \(A = I\)，其中 \(I\) 为 单位阵，满足 \(p^T I q = p^T q = 0\)，则称 \(p\) 和 \(q\) 正交。

共轭向量组：

若存在 一组非零向量 \(\{p_i\}, i = 1, 2, ... , m\)关于对称阵 \(A\) 共轭，即：

\[p^T_iAp_j = 0, \quad i \not = j \]

则称这组向量 \(\{p_i\}, i = 1, 2, ... , m\) 为 共轭向量组。

---

2. 共轭方向法

2.1 共轭方向法与梯度下降法

对于一个 二次型优化问题：

\[f(x) = \frac{1}{2}x^T A x \]

一般情况下，分别用 梯度下降法（GD） 和 共轭方向法（CG），有如下图的收敛轨迹：

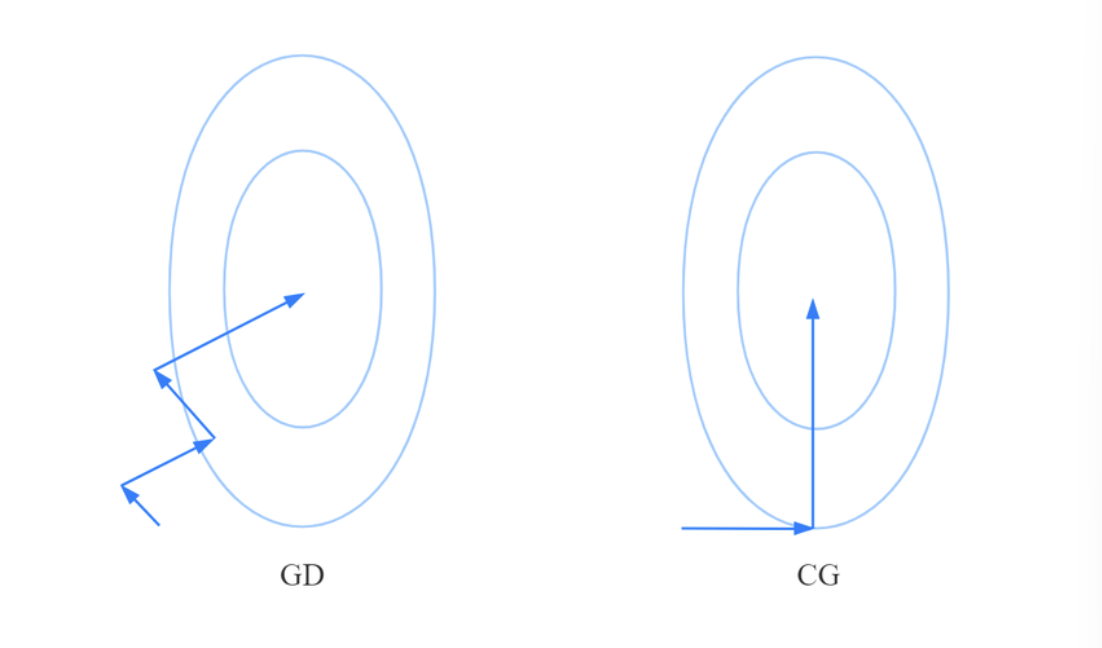
显然可以看出，梯度下降法需要经过多次迭代，而共轭方向法只需要经过两次迭代。

2.2 共轭方向法定义

假设有两个搜索方向 \(d_1\) 和 \(d_2\)，且有 \(d^T_1 d_2 = 0\)。有空间线性变换矩阵 \(A\)，那么经过线性变换后有：

\[d^T_1 A d_2 = 0 \]

我们可以由上述表达式，来 更新 迭代算法过程中的 搜索方向 \(d^k\)，故有：

\[(d^{k + 1})^TA d^k = 0, \quad k \in \mathbb{R}^+ \]

这就是 共轭方向法 的 搜索方向更新公式。

2.3 共轭方向法基本过程

• 选择初始值 \(x^0\) 以及初始搜索方向 \(d^0\) ，令 \(k = 0\)

• 若满足终止条件 \(||\nabla f(x^k)|| < \varepsilon\)，记 \(x^* = x^k\)，结束整个算法

• 确定步长: \(\alpha_k = \text{arg} \min_{\alpha > 0} f(x^k + \alpha d^k)\)，采用线搜索方法。

• 更新迭代点：$x^{k + 1} = x^k + \alpha_k d^k $

• 更新搜索方向: \(d^{k + 1}\)，使得 \((d^{k + 1})^TAd^k = 0\)

---

3. 共轭梯度法

3.1 共轭梯度

共轭梯度法 下的搜索方向构造需要满足如下条件：

• 所有搜索方向相互共轭

• 搜索方向 \(d^{k+1}\) 是 \(-\nabla f(x^{k + 1})\) 和 \(d^{k}\) 的 线性组合。

故构建的关系如下：

\[d^{k + 1} = - \nabla f(x^{k + 1}) + \beta_{k} d^k \]

由 \(\text{Hestenes-Stiefel}\) 公式 来确定系数 \(\beta\)。对上述等式两边同乘 \((d^k)^TA\)，且有 \((d^k)^T A d^{k + 1} = 0\):

\[\beta_{k}^{\text{HS}} = \frac{\nabla f(x^{k + 1})^T A d^k}{(d^k)^T A d^k} \]

经过一系列修正后，可以得到 \(\text{Fletcher-Reeves}\) 公式：

\[\beta_{k}^{\text{FR}} = \frac{\nabla f(x^{k + 1}) ^{T} \nabla f(x^{k + 1})}{\nabla f(x^k)^T \nabla f(x^k)} \]

这个公式是比较常用的。（想睡觉了，证明很多地方没来得及看明白，所以就速度整整了）

3.2 共轭梯度法基本过程

• 选择初始值 \(x^0\) 以及初始搜索方向 \(d^0 = -\nabla f(x^0)\) ，令 \(k = 0\)

• 若满足终止条件 \(||\nabla f(x^k)|| < \varepsilon\)，记 \(x^* = x^k\)，结束整个算法

• 确定步长: \(\alpha_k = \text{arg} \min_{\alpha > 0} f(x^k + \alpha d^k)\)，采用线搜索方法。(当然，这里可以根据共轭梯度得到步长的迭代表达式 \(\alpha_k = \frac{\nabla f(x^k)^T \nabla f(x^k)}{(d^k)^T A d^k}\)，但是我现在想睡觉了)

• 更新迭代点：$x^{k + 1} = x^k + \alpha_k d^k $

• 计算新梯度 \(\nabla f(x^{k + 1})\)

• 计算系数 \(\beta\): \(\beta_k = \frac{\nabla f(x^{k + 1})^T\nabla f(x^{k + 1})}{\nabla f(x^k)^T\nabla f(x^k)}\)

• 更新搜索方向: \(d^{k + 1}\)，使得 \(d^{k + 1} = - \nabla f(x^{k + 1}) + \beta_{k} d^k\)

---

参考

最优化方法复习笔记（六）共轭梯度法

---

这篇整得挺烂的，共轭梯度法很多地方的证明没太看，而且tmd明天就要考试了！！！

上白泽慧音 老师保佑我 \(\text{da}\)★\(\text{ze}\)