[最优化方法笔记] 线搜索方法

1. 线搜索方法

无约束优化问题求解的基本方法是迭代算法，通过逐步逼近的方法来逼近精确解。

假设精确解所在的点为 $x^*$，初始点为 $x_0$，通过不断迭代 $x^1, x^2, ... x^k$ 使得 $x \rightarrow x^*$。

一般的迭代过程如下：

一般有两种主要的求解方式：

线搜索
- 确定 下降方向：负梯度、牛顿方向、拟牛顿方向...... ( 满足 $\nabla f(x^k)^T d^k < 0$ )
- 确定步长：一些准则......
信赖域

构造一元辅助函数：

\[\phi(\alpha) = f(x^k + \alpha d^k) \]

其中 $d^k$ 是 下降方向，$\alpha > 0$ 是辅助函数的 自变量

选取的 $\alpha$ 尽可能让 $\phi (\alpha_k)$ 小，故有最优化问题：

\[\alpha_k = \text{arg} \min_{\alpha > 0} \phi(\alpha) \]

$\alpha_k$ 为当前的最佳步长。

根据最优解的一阶必要条件，选取的 $\alpha_k$ 满足：

\[\phi ^{'}(\alpha) = \nabla f(x^k + \alpha d^k)^T d^k = 0 \]

根据等式求出解析解，并通过 $\text{Hessen}$ 矩阵判断是否为最优解。

但是，该方法存在一些缺点：

采用 基于搜索区间 的 直接搜索法，要求事先知道一个包含最优解 $ \alpha_k$ 的搜索区间。

设 $\alpha_k$ 是 $\phi(\alpha)$ 的极小点，若存在区间 $[l, r]$ ，使得 $\alpha_k \in [l, r]$ ，并且要求 $\phi(\alpha)$ 在此区间是 单峰函数。

搜索区间的确定：

一般采用 进退算法 确定 初始的搜索区间 和 初始点 。进退算法的步骤一般如下：

任选一个初始点 $\alpha_0$ 和初始步长 $h > 0$，计算 $\phi(\alpha_0)$
向前进一步搜索得到 $\alpha_0 + h$，如果该点的目标函数值较之前减小，那么加大步长 $h$，并继续向前搜索；如果反而减小了，那么取步长 $h = -h$，向反方向进行搜索。
不断迭代得到一个确定的区间 $[l, r]$，并设定初始点为 $\frac{l + r}{2}$

常见的直接搜索法：

求解 $\phi(\alpha)$ 的精确解会导致计算量很大，而且有时候复杂的导数表达式使得难以求解。

可以适当放松对 $\alpha_k$ 的要求，只要求满足适当的条件即为 $\phi(\alpha)$ 的最优解。

$\text{Armijo}$ 准则

步长 $\alpha$ 满足 $\text{Armijo}$ 准则即：

\[f(x^k + \alpha d^k) \le f(x^k) + c_1 \alpha \nabla f(x^k)^Td^k \]
其中 $d^k$ 为点 $x^k$ 处的下降方向，$c_1 \in (0, 1)$ 是一个常数。

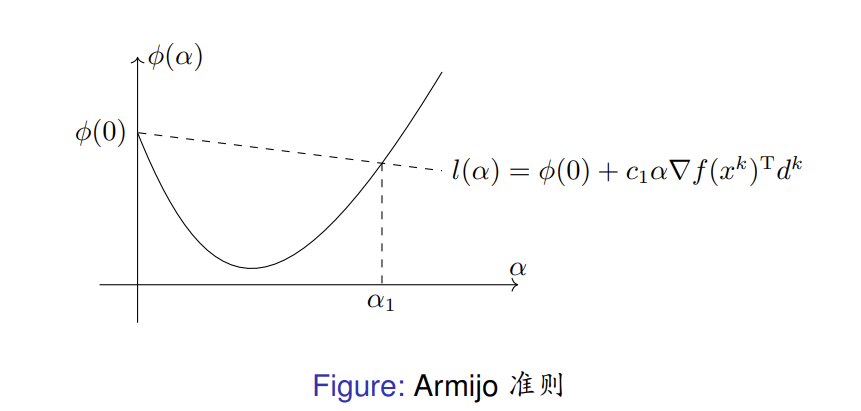
可以看出，点 $(\alpha, \phi(\alpha))$ 位于直线 $l(\alpha) = \phi(0) + c_1 \alpha \nabla f(x^k)^Td^k$ 的下方，区间 $[0, \alpha_1]$ 内的所有点均满足 $\text{Armijo}$ 准则。

通常 $c_1$ 是一个很小的正数，例如 $c_1 = 10^{-3}$

$\text{Goldstein}$ 准则

步长 $\alpha$ 满足 $\text{Goldstein}$ 准则即：

\[\begin{split} & f(x^k + \alpha d^k) \le f(x^k) + c \alpha \nabla f(x^k)^T d^k \\\\ & f(x^k + \alpha d^k) \ge f(x^k) + (1 - c)\alpha \nabla f(x^k)^Td^k \end{split} \]
其中 $d^k$ 为点 $x^k$ 处的下降方向，$c \in (0, \frac{1}{2})$ 是一个常数。

可以看出，区间 $[\alpha_1, \alpha_2]$ 内的点位于直线 $l_1(\alpha) = \phi(0) + c \alpha \nabla f(x^k)^Td^k$ 的下方，而位于 $l_2(\alpha) = \phi(0) + (1-c) \alpha \nabla f(x^k)^Td^k$ 上方。

$\text{Wolfe}$ 准则

步长 $\alpha$ 满足 $\text{Wolfe}$ 准则即：

\[\begin{split} & f(x^k + \alpha d^k) \le f(x^k) + c_1 \alpha \nabla f(x^k)^T d^k \\\\ & \nabla f(x^k + \alpha d^k)^T d^k \ge c_2 \alpha \nabla f(x^k)^Td^k \end{split} \]
其中 $d^k$ 为点 $x^k$ 处的下降方向，$c_1, c_2 \in (0, 1)$ 是常数，且 $c_1 < c_2$。

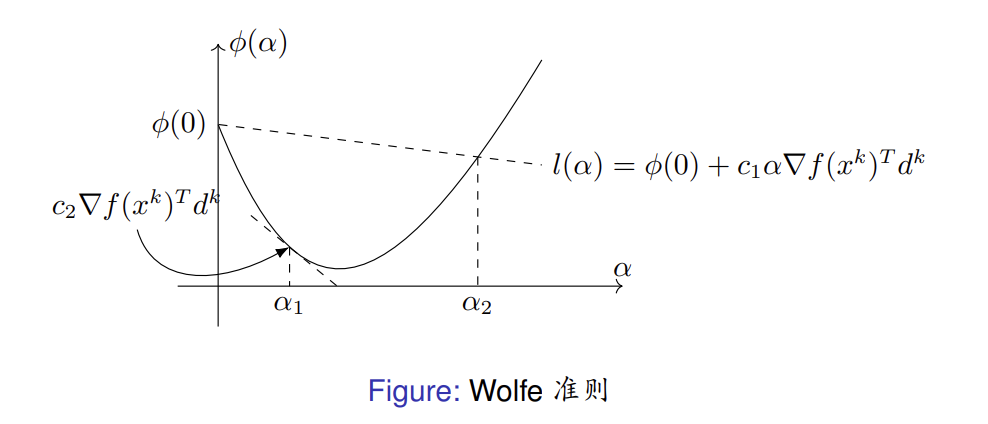
$\nabla f(x^k + \alpha d^k)^T d^k$ 恰好就是 $\phi(\alpha)$ 的导数，要求 $\phi (\alpha)$ 在点α 处切线的斜率不能小于 $\phi ^{'} (0)$ 的 $c_2$ 倍。

$\phi(\alpha)$ 的极小值点 $\alpha^*$ 处有 $\phi^{'}(\alpha^*) = \nabla f(x^k + \alpha^* d^k)^T d^k = 0$，且永远满足条件二。

选择较小的 $c_1$ 可使得 $\alpha^*$ 同时满足条件一。$\text{Wolfe}$ 准则在绝大多数情况下会包含线搜索子问题的精确解。