[最优化方法笔记] 凸集、凸函数、凸优化

1. 凸集

1.1 凸集的几何定义

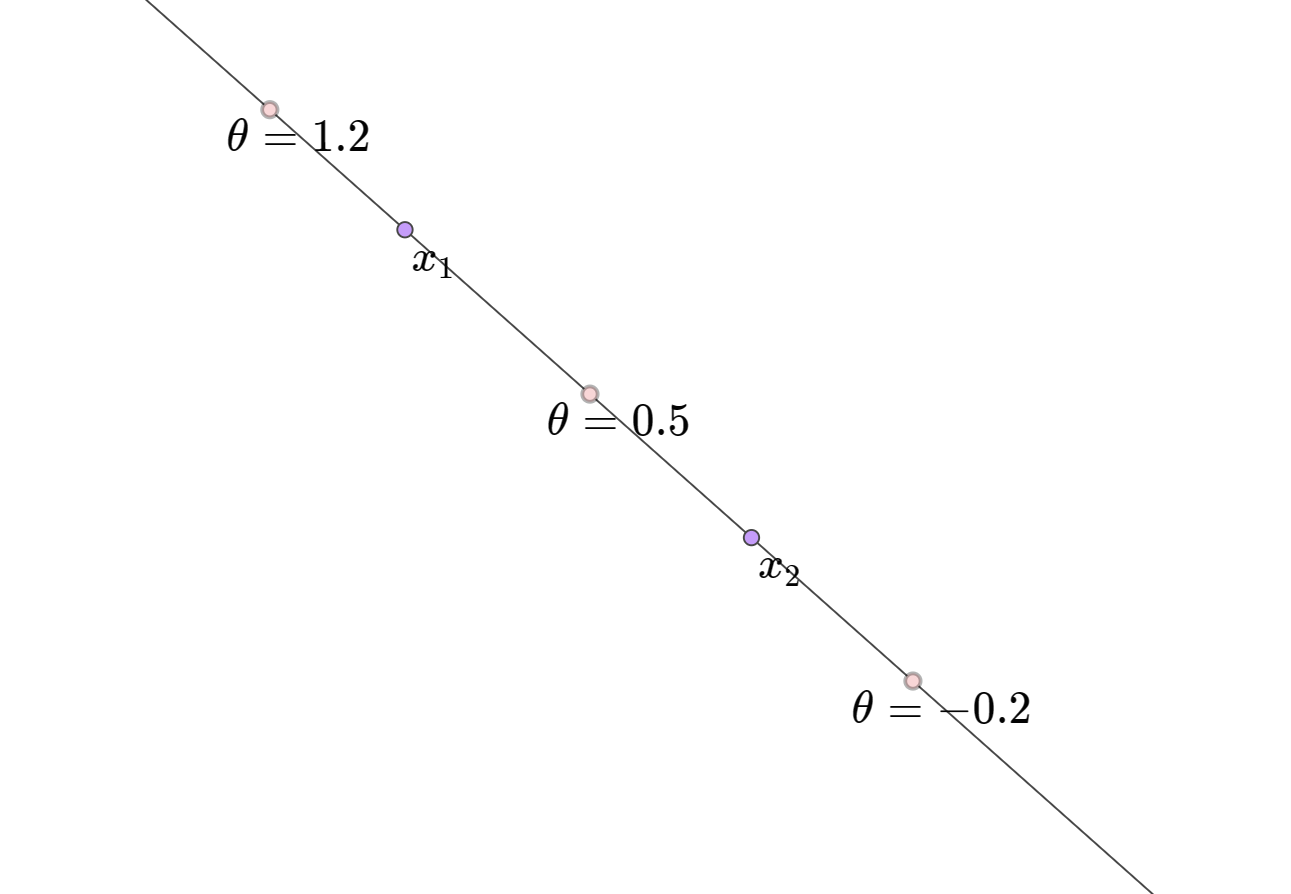
在 \(\mathbb{R}^n\) 空间中，经过两个不同的点 \(x_1\) 和 \(x_2\) 可以确定一条直线，方程如下：

\[y = \theta x_1 + (1 - \theta)x_2, \; \theta \in \mathbb{R} \]

特别地：

• 当 \(\theta = 0\) 时，\(y = x_2\)

• 当 \(\theta = 1\) 时，\(y = x_1\)

• 当 \(0 \le \theta \le 1\) 时，\(y\) 是点 \(x_1\) 和 \(x_2\) 之间构成的 线段 上的点

• 当 \(\theta < 0\) 或 \(\theta > 1\) 时，点 \(y\) 是在 \(x_1\) 和 \(x_2\) 构成的 直线上 的但是在所构成 线段之外 的点。

仿射集:

如果经过集合 \(\mathcal{C}\) 的任意两个点的直线都在 \(\mathcal{C}\) 内，则称 \(\mathcal{C}\) 为 仿射集 。

\[x_1, x_2 \in \mathcal{C} \Rightarrow \theta x_1 + (1 - \theta)x_2 \in \mathcal{C}, \; \forall \theta \in \mathbb{R} \]

凸集:

如果经过集合 \(\mathcal{C}\) 的任意两个点的 线段 都在 \(\mathcal{C}\) 内，则称 \(C\) 为 凸集 。

\[x_1, x_2 \in \mathcal{C} \Rightarrow \theta x_1 + (1 - \theta)x_2 \in \mathcal{C}, \; \forall \; 0 \le \theta \le 1 \]

显然，仿射集 都是 凸集 。

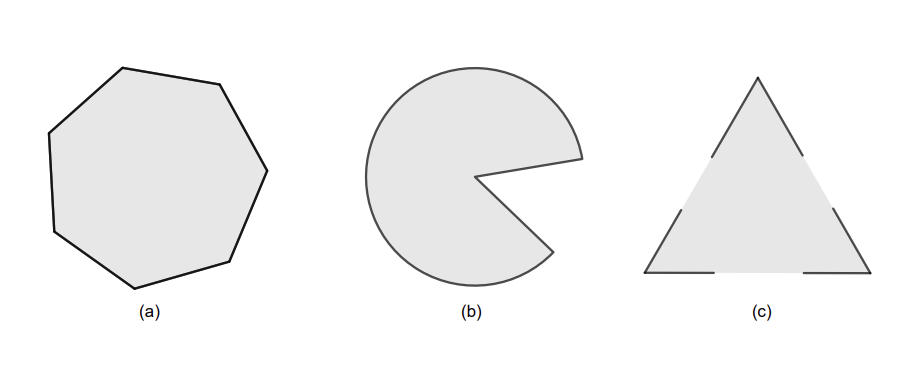
上图中的 (a) 为 凸集，而 (b), (c) 不是凸集。

其中，(b) 存在空隙，显然不是凸集；(c) 存在一些边不在集合中，故也不是凸集。

1.2 凸集的性质

• 若 \(\mathcal{S}\) 为凸集，则 \(k \mathcal{S} = \{ks | k \in \mathbb{R}, s \in \mathcal{S} \}\) 也是凸集

• 若 \(\mathcal{S}\) 和 \(\mathcal{T}\) 都是凸集，则 \(\mathcal{S} + \mathcal{T} = \{s + t | s \in \mathcal{S}, t \in \mathcal{T} \}\) 也是凸集

• 若 \(\mathcal{S}\) 和 \(\mathcal{T}\) 都是凸集，则 \(\mathcal{S} \cap \mathcal{T}\) 也是凸集。任意多凸集的交都是凸集

• 凸集的内部和闭包都是凸集

---

2. 凸函数

2.1 凸函数定义

凸函数：

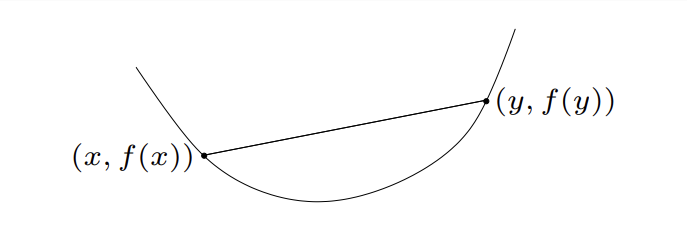
\(f: \mathbb{R}^n \rightarrow \mathbb{R}\) 为适当函数，函数 \(f\) 的 定义域 为 凸集 且

\[f(\theta x + (1 - \theta)y) \le \theta f(x) + (1 - \theta)f(y) \]

对于所有的 \(x, y \in \text{dom} f, \; 0 \le \theta \le 1\) 都成立（dom即定义域），那么称 \(f\) 为 凸函数 。

• 若 \(f\) 为凸函数，则 \(-f\) 为 凹函数

• 若对于所有 \(x, y \in \text{dom} f, \; x \not = y, \; 0 < \theta < 1\) 有

  \[f(\theta x + (1 - \theta)y) < \theta f(x) + (1 - \theta)f(y) \]

  则称 \(f\) 为 严格凸函数

凸函数举例：

• 一元凸函数

  • 仿射函数: 对任意 \(a, b \in \mathbb{R}，ax + b\) 是\(\mathbb{R}\) 上的凸函数

  • 指数函数：对任意 \(a \in \mathbb{R}\)，\(e^{ax}\) 是 \(\mathbb{R}\) 上的凸函数

  • 幂函数：对 \(a \ge 1\) 或 \(a \le 0\)，\(x^a\) 为 \(\mathbb{R}_{+}\) 上的凸函数

• 多元凸函数

  • 仿射函数：\(f(x) = a^Tx + b\)

  • 范数：\(||x||_p = (\sum_{i=1}^n |x_i|^p)^{\frac{1}{p}}, \; p \ge 1\)

2.2 凸函数判定条件

一阶条件：

对于定义在凸集上的 可微函数 \(f\)，\(f\) 是凸函数当且仅当 \(f(y) \ge f(x) + \nabla f(x)^T (y - x) \quad \forall\;x, y \in \text{dom} f\)

显然，凸函数永远位于其切线的上方。

二阶条件：

对于定义在凸集上的 二阶可微函数 \(f\)，\(f\) 是凸函数当且仅当

\[\nabla ^2 f(x) \succeq 0, \quad \forall \; x \in \text{dom} f \]

显然，函数 \(f\) 的导数是 非递减的。

如果 \(\nabla ^2 f(x) \succ 0, \quad \forall \; x \in \text{dom} f\)，则 \(f\) 是 严格凸函数 。

---

3. 凸优化

3.1 凸优化问题

凸优化问题 要求目标函数为凸函数，定义域为凸集。

\[\begin{split} & \min \; f(x) \\ & \; \text{s.t.} \quad g_i(x) \le 0, \quad i = 1, ... , m \\ & \;\; \qquad Ax = b \end{split} \]

其中 目标函数 \(f\) 和 不等式约束 \(g_i\) 均为 凸函数；等式约束 均为 仿射函数。

3.2 凸优化问题最优解

凸优化问题的 任意局部极小点 都是 全局最优 。

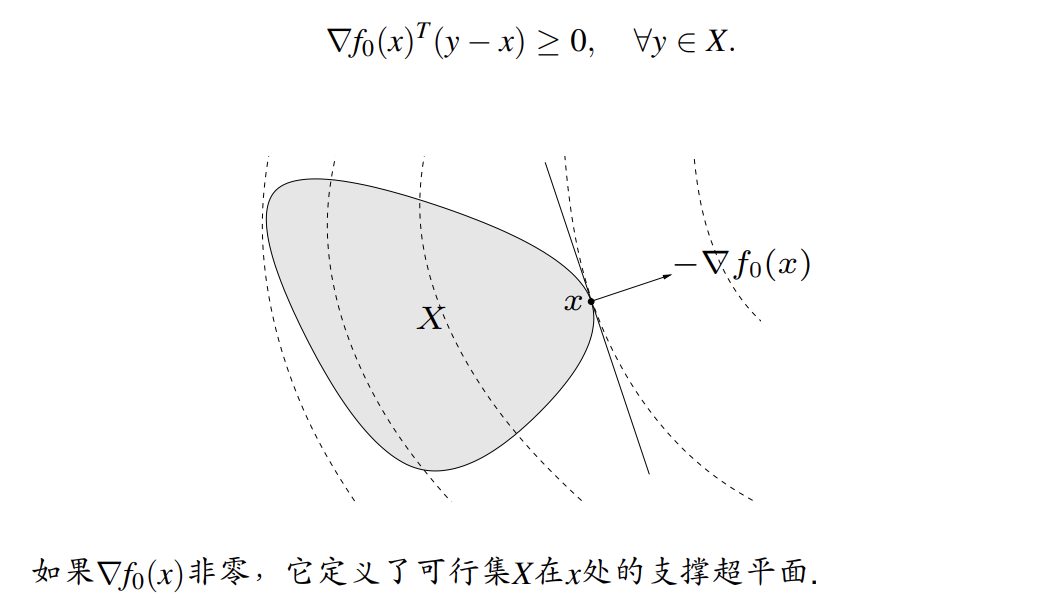
\(x\) 是凸优化问题 \(\min_{x\in X} f(x)\) 的最优解当且仅当 \(x\) 可行且

\[\nabla f(x)^T (y - x) \ge 0, \; \forall y \in X \]

可以由凸函数判定 一阶条件 得出此结论。

3.3 常见凸优化问题

• 线性规划 (\(\text{LP, Linear Program}\))

  \[\begin{split} & \min_{x \in \mathbb{R}^n} \; c^Tx \\ & \; \text{s.t.} \quad Gx \le e, \\ & \;\; \qquad Ax = b \end{split} \]

  其中 \(c \in \mathbb{R}^n, \; A \in \mathbb{R}^{m \times n}, \; b \in \mathbb{R}^m, \; G \in \mathbb{R}^{p \times n},\;e \in \mathbb{R}^p\)

• 二次规划 (\(\text{QP, Quadradic Program}\))

  \[\begin{split} & \min \; \frac{1}{2}x^T P x + q^Tx + r \\ & \; \text{s.t.} \quad Gx \le e, \\ & \;\; \qquad Ax = b \end{split} \]

  目标函数是凸二次型的

3.4 凸优化一般求解

凸优化问题中局部最优解即全局最优解，故求解过程可以简化为：找到一个点使得目标函数值持续减少，直到触发停止条件或达到一个最小值。

\[x_{k + 1} = x_k + \alpha_k d_k \]

其中 \(x_k\) 为 第 \(k\) 次迭代的值，\(d_k\) 为 第 \(k\) 次迭代时的搜索方向，\(\alpha_k\) 为 第 \(k\) 次迭代的步长。

搜索方向满足：

• \(\nabla f(x_k)^T d_k < 0\)，即沿着梯度相反的方向进行搜索

• \(f(x_{k + 1}) = f(x_k + \alpha_k d_k) < f(x_k)\)

---

参考

刘浩洋, 户将, 李勇锋, 文再文 《最优化：建模、算法与理论》

Convex Optimization——凸函数

机器学习必知必会：凸优化