[数字图像处理笔记] 第八章 图像分割

1. 概述

图像分割 是图像识别和图像理解的 前提 步骤，图像分割质量的好坏直接影响图像处理的结果。

图像分割是将一幅图像分解为若干互不相交、有意义的、具有 相同性质 的区域。

  • 分割出来的各区域在灰度、纹理等方面具有相似性，区域内部是连通的

  • 区域边界是明确的

  • 相邻区域对分割所依据的性质有明显的差异


图像分割算法一般是基于灰度值 不连续性 和 相似性 的。

  • 基于亮度的 不连续性变化 分割图像，比如 图像的边缘

  • 基于事先预定的准则将图像分割为 相似区域


2. 边缘检测和连接

2.1 边缘检测

  • 边缘

    边缘图 可以用 表示边缘点位置 的 二值图像 来表示。

    边缘图通过 边缘点连接 完成物体的检测，勾画出各个物体的轮廓。

    边缘的一些特性：

    • 根据人类视觉特性，首先感受到的是边缘

    • 在边缘处，灰度和结构等信息发生 突变

    • 边缘可以是一个区域的结束，也可以是一个区域的开始。利用这个特性来分割图像。

    边缘上的突变，可以用 微分算子 进行检测。



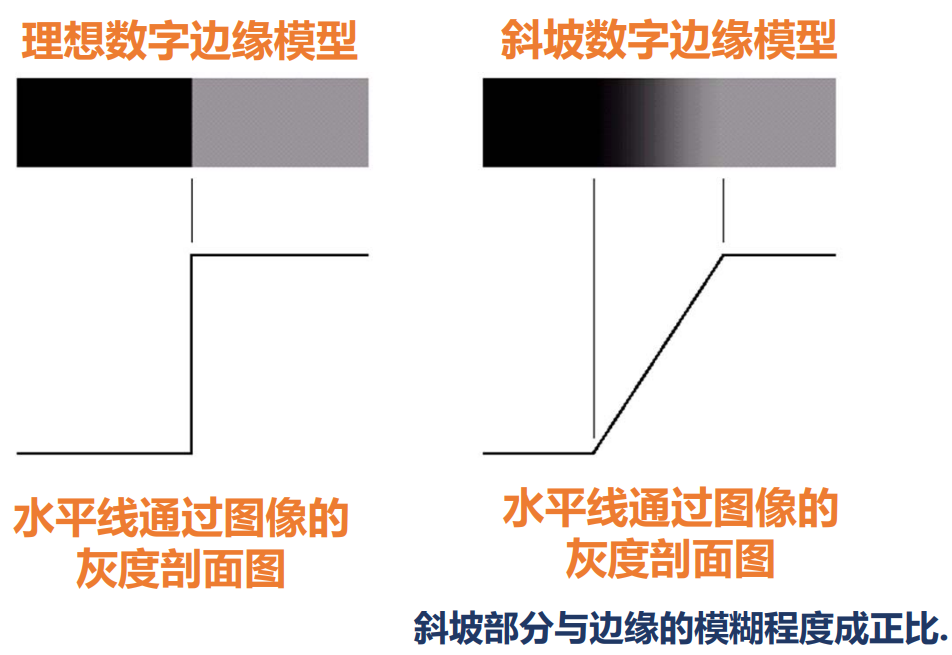
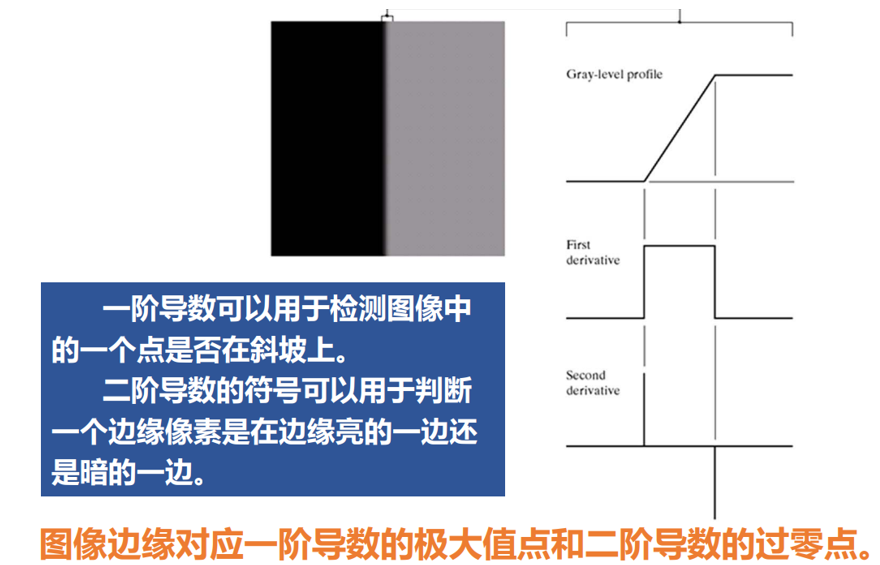
  • 梯度算子

    • 一阶导数算子

      \[\nabla f(x, y) = \begin{bmatrix} G_x \\\\ G_y \end{bmatrix} = \begin{bmatrix} \frac{\partial f}{\partial x} \\\\ \frac{\partial f}{\partial y} \end{bmatrix} \]

    • \(\text{Roberts}\) 算子

    • \(\text{Prewitt}\) 算子

    • \(\text{Sobel}\) 算子


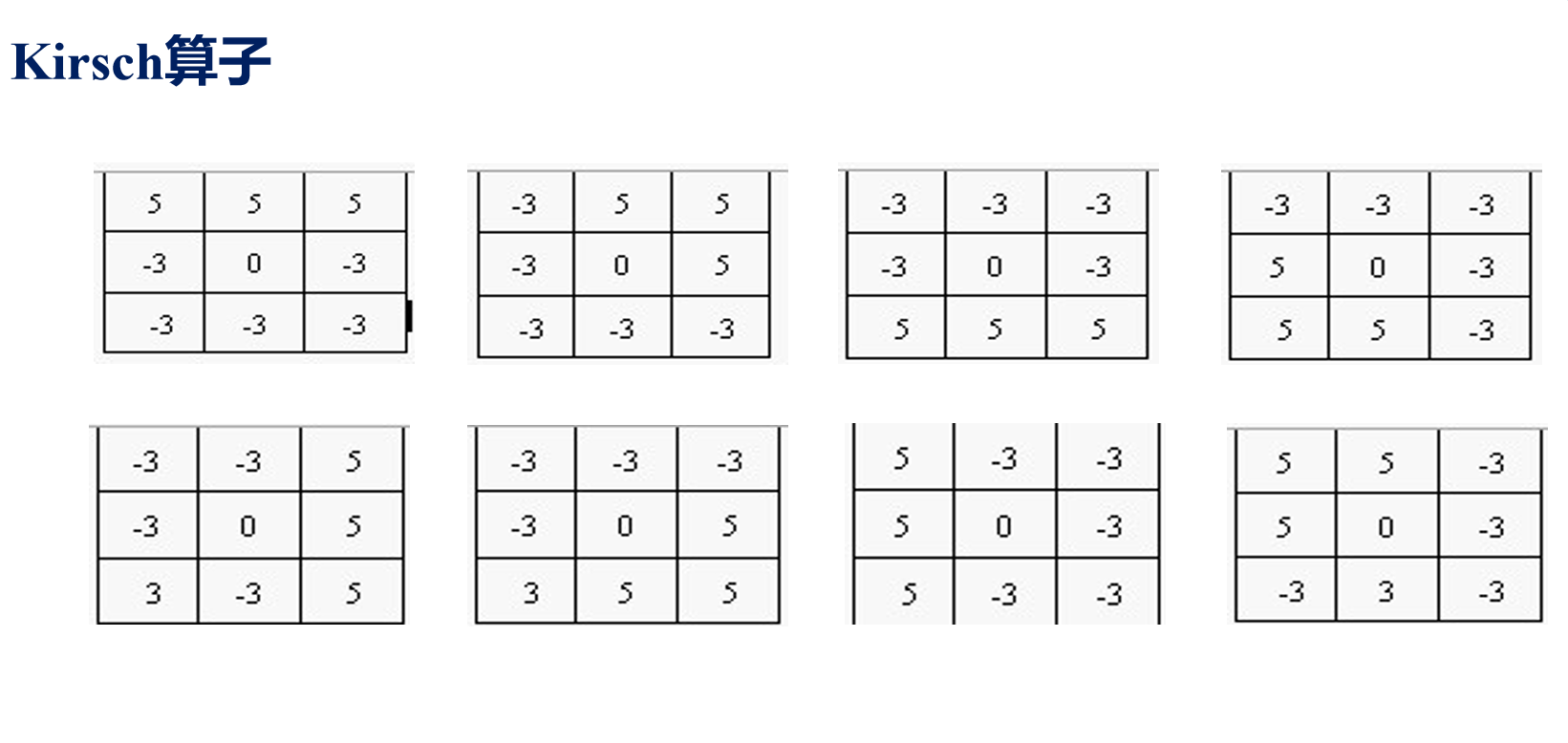
  • Kirsch算子

    图像中的每个点均与这8个模板进行卷积，每个掩模对某个特定边缘方向作出最大响应。

    所有8个方向中的 最大值 作为边缘幅度图像的输出。

    最大响应掩模的序号构成了对边缘方向的编码。

    \[G(x, y) = \max(|M_1|, |M_2|, ... , |M_8|) \]

    (一个模板，8个角度)


  • 拉普拉斯算子

  • 算子性能检测

相关代码：

I = imread('1.png');
I = rgb2gray(I);

figure;
imshow(I), title('initial img');

figure;
I1 = edge(I, 'roberts');
subplot(2, 2, 1);
imshow(I1), title('roberts');

I2 = edge(I, 'prewitt');
subplot(2, 2, 2);
imshow(I2), title('prewitt');

I3 = edge(I, 'sobel');
subplot(2, 2, 3);
imshow(I3), title('sobel');

I4 = edge(I, 'log');
subplot(2, 2, 4);
imshow(I4), title('log');

  • \(\text{Roberts}\) 算子：

    \(\text{Roberts}\) 算子利用 局部差分 算子寻找边缘，边缘定位精度较高，但容易丢失一部分边缘，不具备抑制噪声的能力。

    该算子对 具有陡峭边缘 且 含噪声少 的图像 效果较好。

  • \(\text{Sobel}\) 算子和 \(\text{Prewitt}\) 算子

    都是对图像 先做加权平滑 处理，然后再做 微分 运算，所不同的是平滑部分的权值有些差异，因此 对噪声具有一定的抑制 能力，但不能完全排除检测结果中出现的虚假边缘。

    虽然这两个算子边缘定位效果不错，但 检测出的边缘容易出现多像素宽度。

  • \(\text{Laplacian}\) 算子

    是不依赖于边缘方向的 二阶微分 算子，对图像中的阶跃型边缘点定位准确，该算子 对噪声非常敏感，它使噪声成分得到加强，这两个特性使得该算子容易丢失一部分边缘的方向信息，造成一些不连续的检测边缘，同时 抗噪声能力比较差。

  • \(\text{LOG}\) 算子

    该算子首先用 高斯函数 对图像作 平滑滤波 处理，然后才使用 Laplacian算子 检测 边缘，因此克服了Laplacian算子抗噪声能力比较差的缺点，但是在抑制噪声的同时也可能将原有的比较尖锐的边缘也平滑掉了，造成这些尖锐边缘无法被检测到。


2.2 边缘连接

利用前面的方法检测出边缘点，但由于 噪声、光照不均等因素 的影响，获得边缘点有 可能是不连续 的，必须使用连接过程将边缘像素组合成有意义的边缘信息，以备后续处理。

在邻域中找出其它端点并填充上必要的边界像素，从而将它们连接起来。

这种方法可能会对图像过度分割。为了避免过度的分割，可以规定：两个端点只有在边缘强度和走向相近的情况下才能连接。

...


3. 阈值分割

将所有灰度值 大于或等于 某阈值的像素都判为物体；

将所有灰度值 小于 该阈值的像素排除在物体之外。

...


4. 区域分割

阈值分割法由于没有或很少考虑空间关系，该方法应用受到限制。

区域分割法 可以弥补这点不足，它利用的是图像的空间性质，该方法认为分割出来的属于同一区域的像素应具有相似的性质，其概念是相当直观的。

传统的区域分割算法有 区域生长法 和 区域分裂合并法。该类方法在没有先验知识可以利用时，对含有复杂场景或自然景物等先验知识不足的图像进行分割，也可以取得较好的性能。但是，空间和时间开销都比较大。

4.1 区域生长法

区域生长法是一种根据事先定义的准则将像素或子区域聚合成更大区域的过程，该方法主要考虑像素及其 空间邻域 像素之间的关系。

  • 开始时确定 一个或多个像素点 作为 种子。

  • 然后按某种相似性准则增长区域，逐步生成具有某种均匀性的空间区域，将 相邻的具有相似性质 的像素或区域归并从而逐步增长区域，直至没有可以归并的点 或其它 小区域为止。

  • 区域内像素的相似性度量可以包括平均 灰度值、纹理、颜色 等信息。

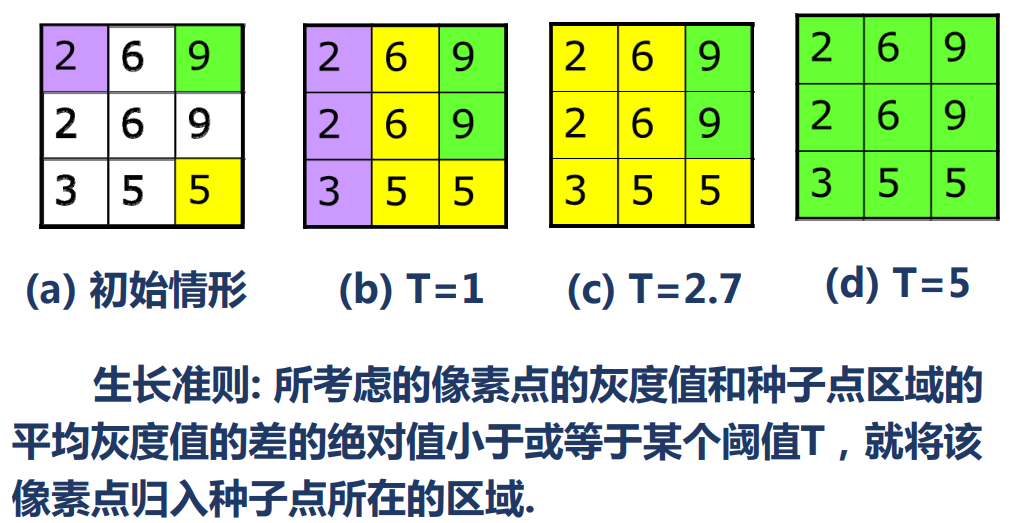
就是 \(bfs\) 求连通块


4.2 区域分裂法

如果区域的某些特性差别比较大，即不满足一致性准则时，则区域应该采用分裂法。

分裂过程从从图像的 最大区域开始，一般情况下，是从整幅图像开始。

  • 确定 分裂准则(一致性准则)

  • 确定 分裂方法，即如何分裂区域，使得分裂后的子区域的特性尽可能都满足一致性准则。


4.3 区域合并法

单纯的区域分裂只能把图像分成许多满足一致性谓词的区域，相邻的具有相同性质的区域并没有合成一体。

  • 合并运算就是把相邻的 具有相似性质的区域合成为一个区域。

  • 合并算法中最重要的运算是确定两个区域的相似性。

  • 可以基于区域的 灰度值，也可以基于 区域边界的强弱性 等因素评判区域的相似度。


4.4 区域分裂合并法

区域分裂合并法无需预先指定种子点，它 按某种一致性准则分裂或者合并区域。

可以先进行分裂运算，然后再进行合并运算；也可以分裂和合并运算同时进行，经过连续的分裂和合并，最后得到图像的精确分割效果。

...


5. 二值图像处理

二值图像 是只具有两个灰度级的图像，它是数字图像的一个重要子集。

  • 一个二值图像通常是由一个图像分割操作产生的。

  • 如果初始的分割不够令人满意，对二值图像的某些形式的处理通常能提高其质量。

\(bfs\) 求连通块

典型示例：


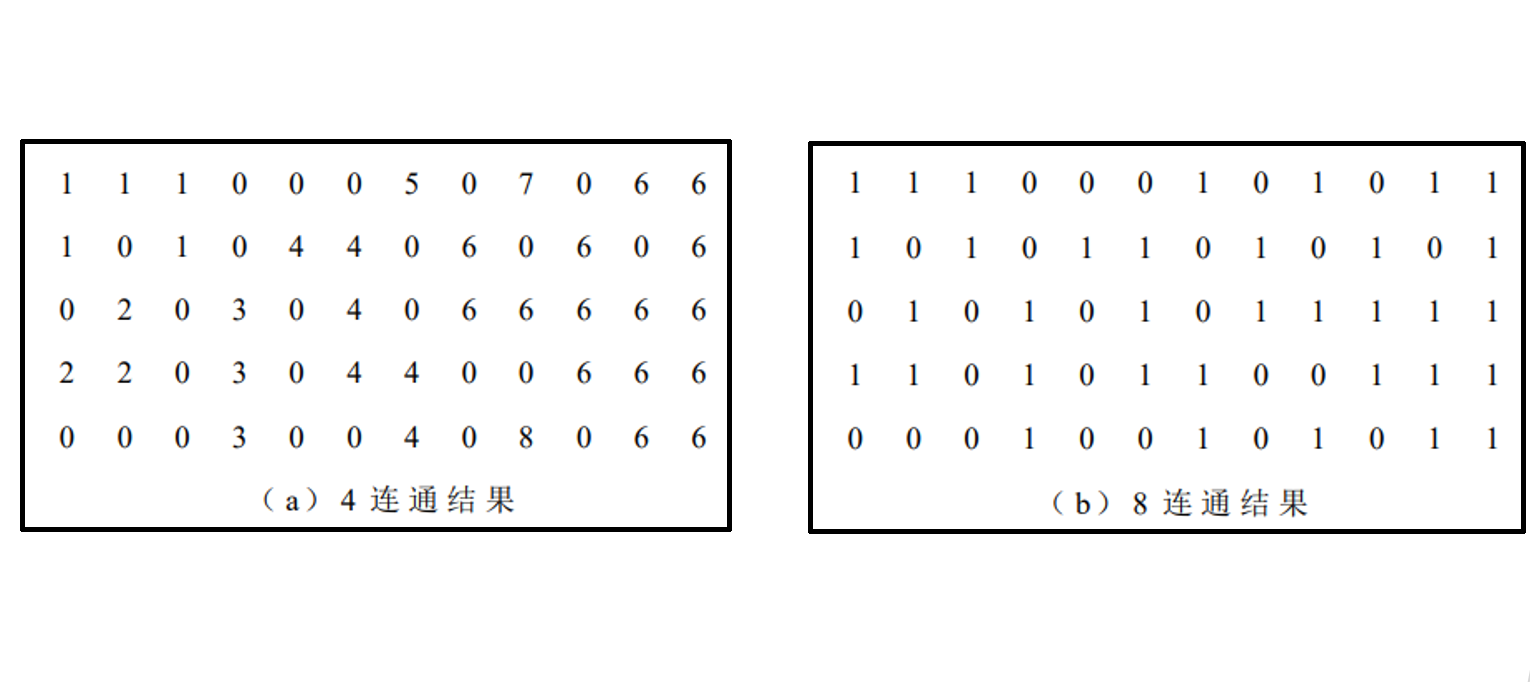
5.1 数学形态学图像处理

  • 腐蚀

\[E = A \Theta B = \{(x, y) | B_{xy} \subseteq A \} \]

其中 \(A\) 是原始图像，\(B\) 为腐蚀的模板。对于每个点 \((x, y)\)，其作为原点的模板块如果完全包含于 \(A\) 中，那么保留这个点。

  • 膨胀

\[D = A \oplus B = \{(x, y) | B_{xy} \cap A \not = \emptyset \} \]

对于每个像素点 \((x, y)\)，用模板 \(B\) 进行扩展。


5.2 开运算和闭运算

  • 开运算：先腐蚀，后膨胀

  • 闭运算：先膨胀，后腐蚀


5.3 一些基本形态学算法

  • 边界提取

    腐蚀操作后保留的物体都是内部的点，用原图像减去腐蚀后的图像，即可得到所有边界像素。

    \[\beta (A) = A - (A \Theta B) \]

    如图所示：

相关代码：

I = imread('1.png');
I = im2bw(I);
subplot(2, 2, 1);
imshow(I), title('bw img');

s = strel('square', 3);
I_erode = imerode(I, s);
I1 = I - I_erode;
subplot(2, 2, 2);
imshow(I1), title('edge img, img - eroded img');

I2 = bwperim(I, 4);
subplot(2, 2, 3);
imshow(I2), title('edge img, use bwperim 4');

I3 = bwperim(I, 8);
subplot(2, 2, 4);
imshow(I3), title('edge img, use bwperim 8');

  • 区域填充

    获取图像边界内的点，并对每个点 \((x, y)\) 使用 结构化元素（模板） \(B\) 进行膨胀操作。由此达到填充区域内部所有点的效果。

    \[X_k = (X_{k-1} \oplus B) \cap A^c \]

    其中 \(A^c\) 是 \(A\) 的补集，\(X_k\) 为当前第 \(k\) 步得到的图像，\(B\) 为结构化元素。


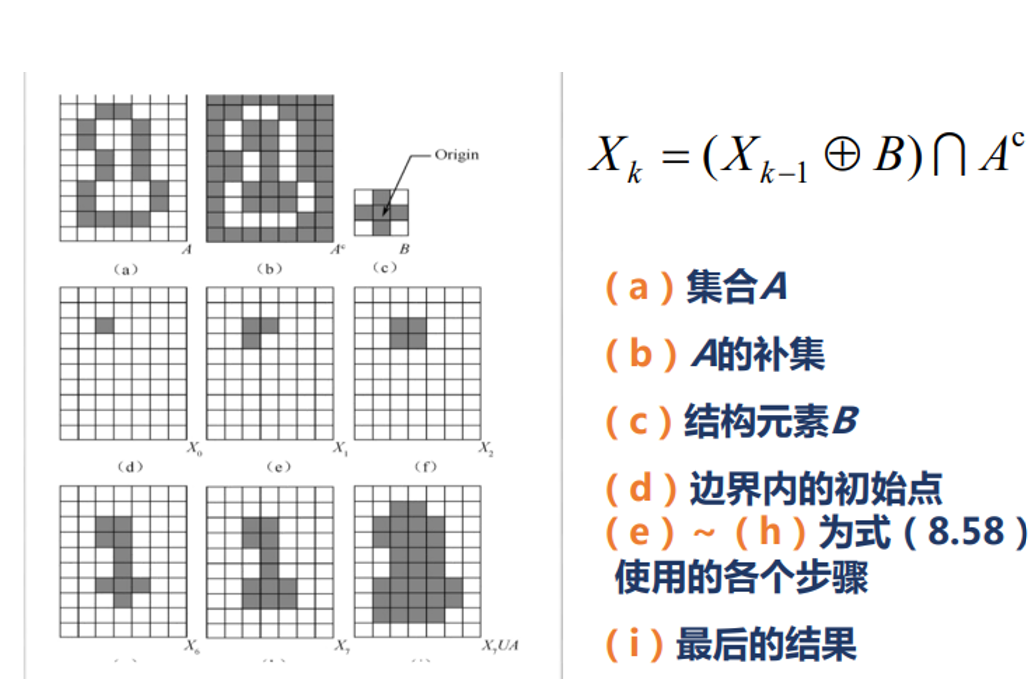
如图所示：

相关代码：

I = imread('2.jpg');
I = im2bw(I);
subplot(1, 2, 1);
imshow(I), title('bw img');

I_fill = bwfill(I, 'holes');
subplot(1, 2, 2);
imshow(I_fill), title('fill img');
posted @ 2023-12-13 02:03  MarisaMagic  阅读(400)  评论(0)  编辑  收藏  举报