[数字图像处理笔记] 第五章 图像增强
1. 图像增强概念和分类
1.1 图像增强的目的
-
改善图像的视觉效果
-
减少 图像中的 噪声,提高 目标与背景的 对比度
-
强调或抑制 图像中的某些 细节
1.2 图像增强分类
-
空间域
-
点处理:灰度变换、直方图处理(均衡化、规定化)、伪彩色处理
-
模板处理:图像平滑、图像锐化
-
-
频率域
-
高通滤波
-
低通滤波
-
同态滤波
-
2. 空间域图像增强
2.1 灰度变换
将输入图像 \(f(x, y)\) 中灰度 \(r\),通过映射函数映射成输出图像 \(g(x, y)\) 中的灰度 \(s\),其运算结果与图像像素位置及被处理像素邻域灰度无关。
其中 \(T\) 为灰度级变换函数。
-
线性变换
\[g(x, y) = af(x, y) + b \]当 \(b=0\) 时:
-
\(a > 1\) : 对比度增加,黑白对比越明显
-
\(a < 1\) : 对比度降低,黑白对比减弱
-
\(a=1\) : 不变
当 \(b \not = 0\) 时:
-
\(b < 0\) : 亮度降低
-
\(b > 0\) : 亮度增加
-
-
分段线性变换
-
反转变换
\[s = -r + (L-1) \]图像灰度级范围为 \([0, L - 1]\)
即将图像进行反色处理
-
对数变换
\[s = c\text{log}_2(1 + r) \] -
幂次变换
\[s = cr^{\gamma} \] -
灰度切分
增强图像中的某个灰度段,其他灰度细节被去掉或保持不变,其目的在于将某个灰度值范围变得比较突出,用于提取图像中的特定细节。
PS: 此部分简略整理了一下,大部分内容在 [数字图像处理笔记] 第三章 图像基本运算 中有。
2.2 直方图处理
2.2.1 直方图
灰度直方图 是图像的一种统计表达,反映了图中不同灰度级出现的统计概率。
假设图像有 \(L\) 个灰度级,灰度级范围是 \([0, L - 1]\),第 \(k\) 个灰度级 \(n_k\) 出现的次数为:
概率为:
如图所示:
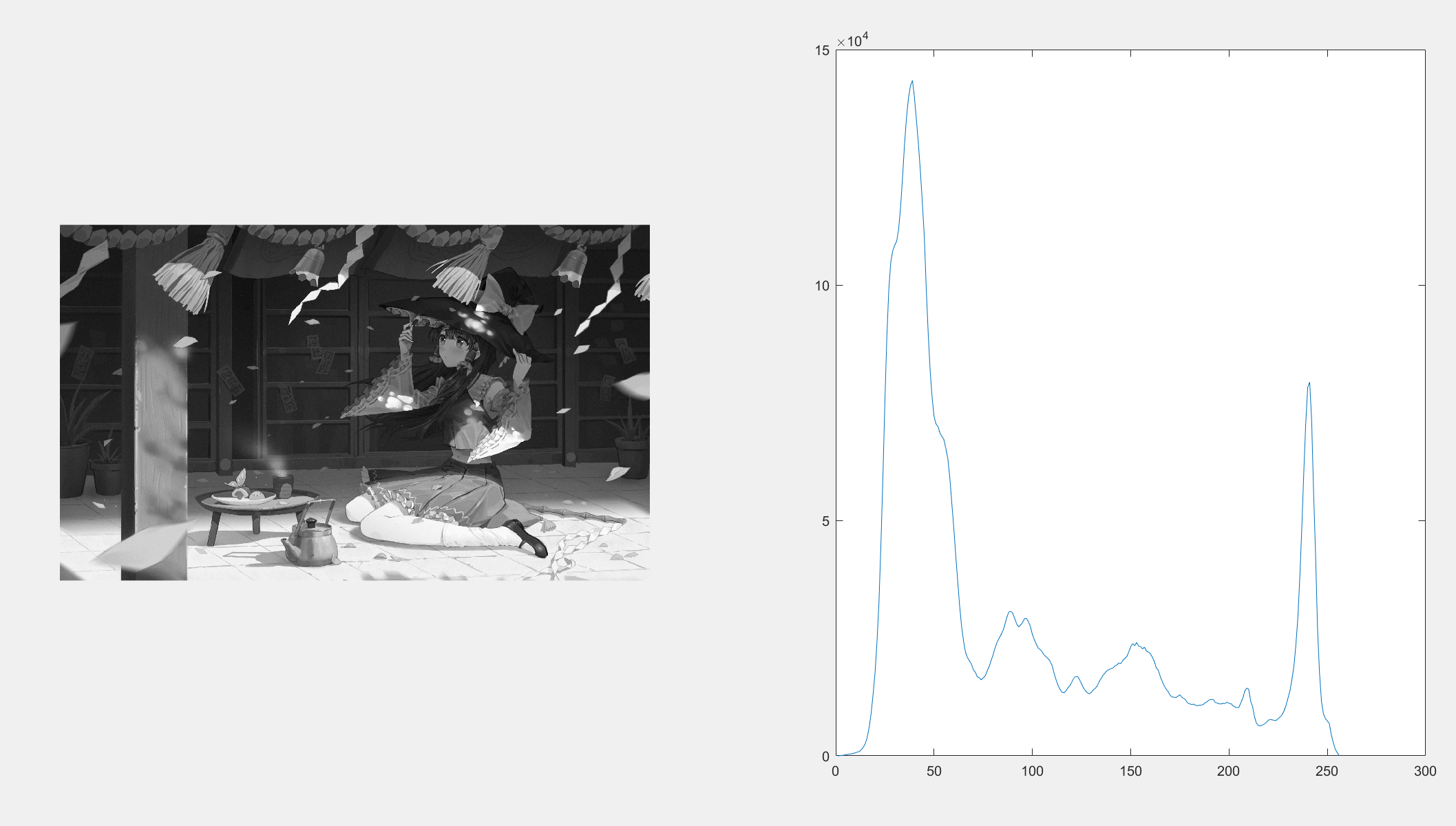
相关代码:
I = imread('2.jpg');
I = rgb2gray(I);
for i=1:256
h(i) = sum(sum(I==i-1));
% fprintf("%d\n", sum(sum(I==i-1)));
end
subplot(1, 2, 1);
imshow(I);
subplot(1, 2, 2);
plot(h);
通过直方图可以看出图像整体性质
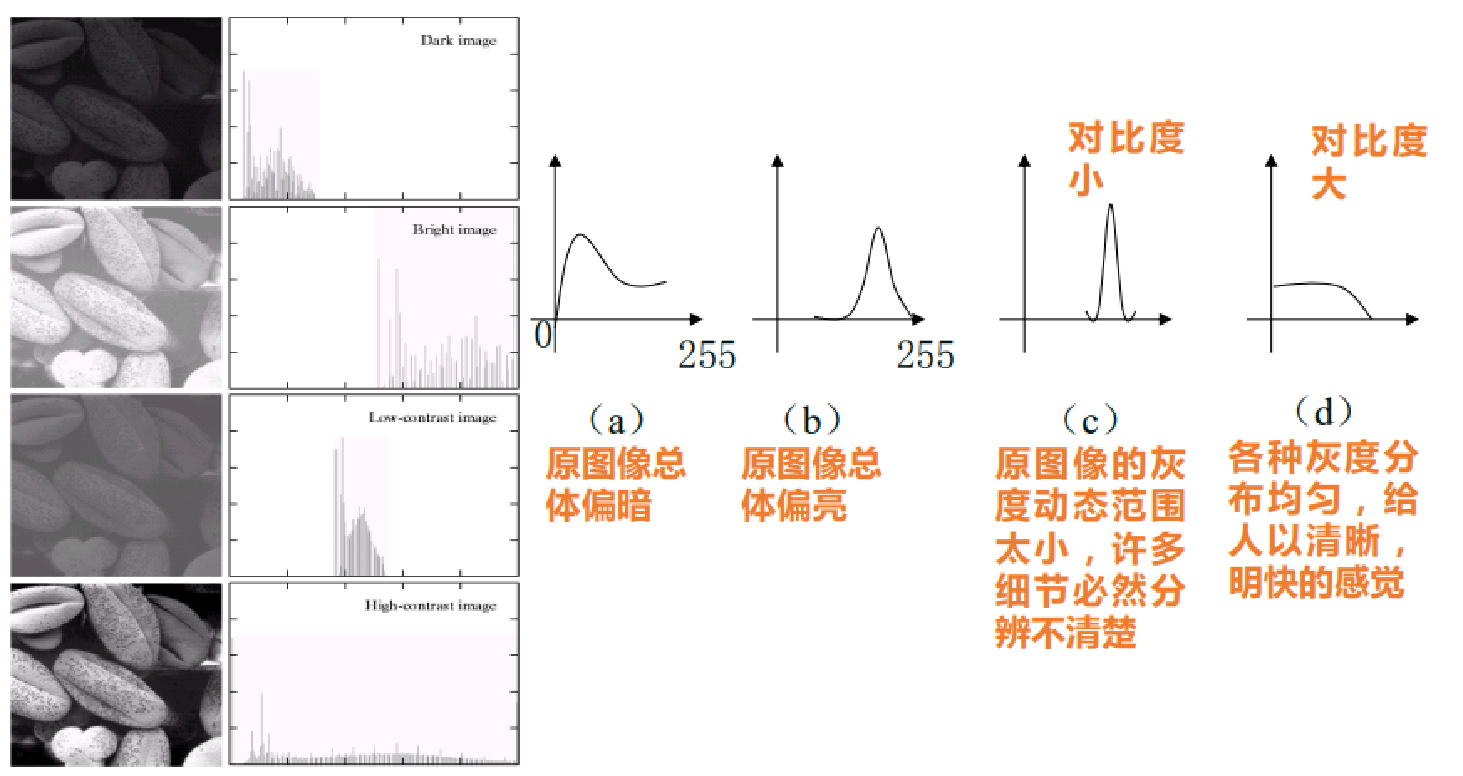
2.2.2 直方图均衡化
把 原始图像的直方图 变换为 均匀分布 的形式,从而增加图像灰度的动态范围,达到增强图像对比度的效果。
经过均衡化处理的图像,其灰度级出现的概率相同,此时图像的熵最大,图像所包含的信息量最大。
计算步骤:
-
统计原始图像的直方图
\[p_r(r_k) = \frac{n_k}{n} \]其中 \(r_k\) 是归一化的输入图像灰度级, \(0 \le r_k \le 1\)。
-
计算直方图累积分布曲线
\[s_k = (L - 1)\sum_{i=0}^kp_r(r_i) = (L-1)\sum_{i=0}^k \frac{n_i}{n} \] -
用累积分布函数作为变换函数进行图像灰度级变换。
重新定位累积分布函数 \(s_k\),与归一化的灰度级 \(r_k\) 进行比较,寻找 最接近的一个 作为原灰度级 \(k\) 变换后的新灰度级。
下表为书上的示例:
一幅64×64像素的图像,灰度级数为8
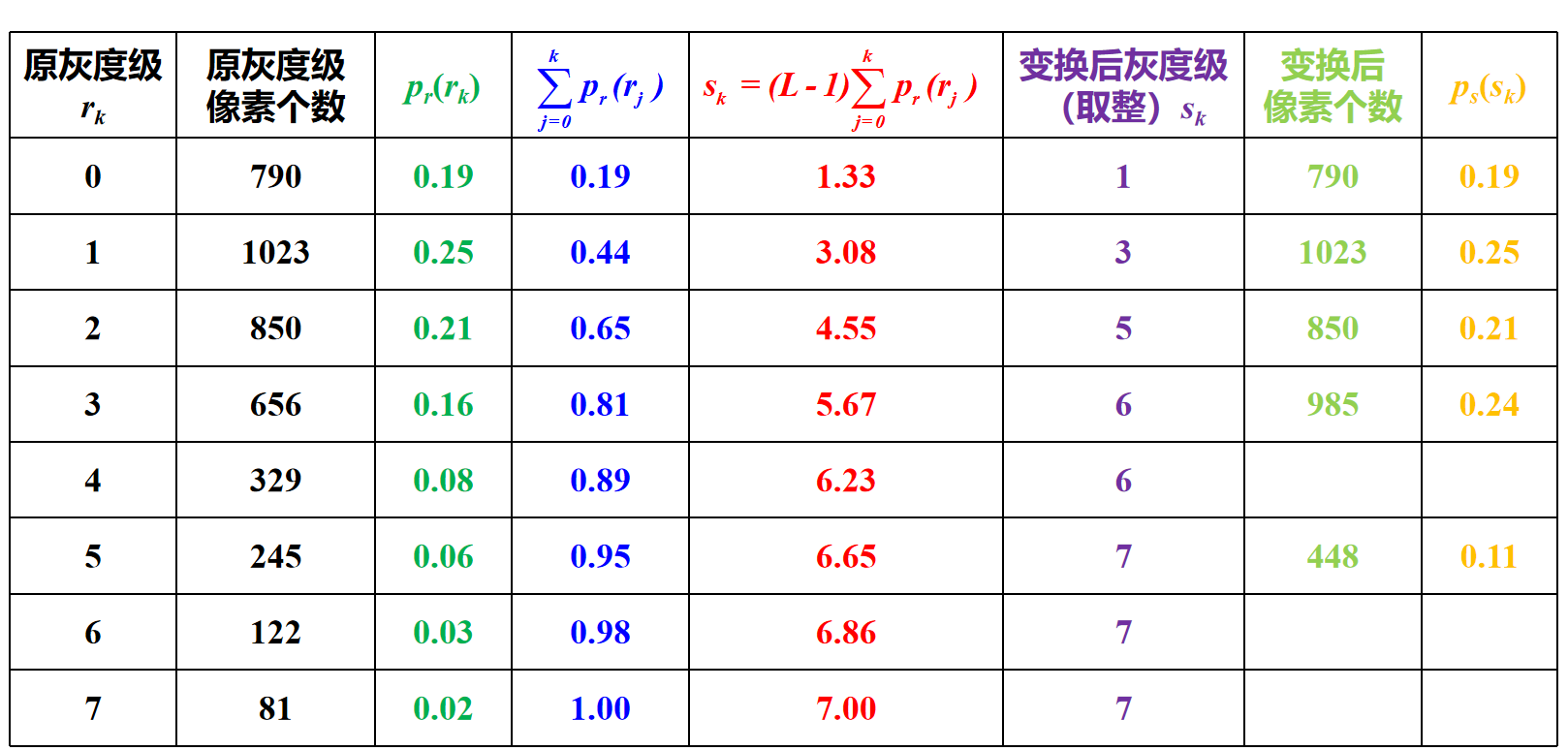
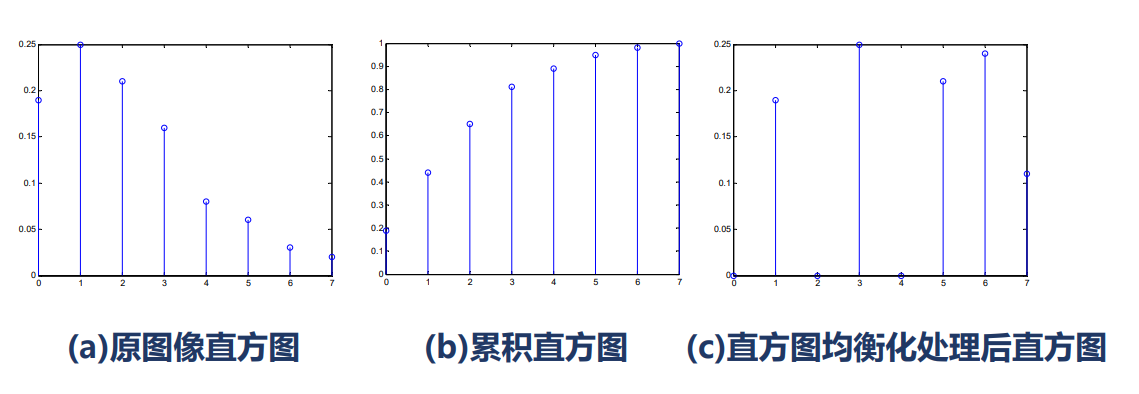
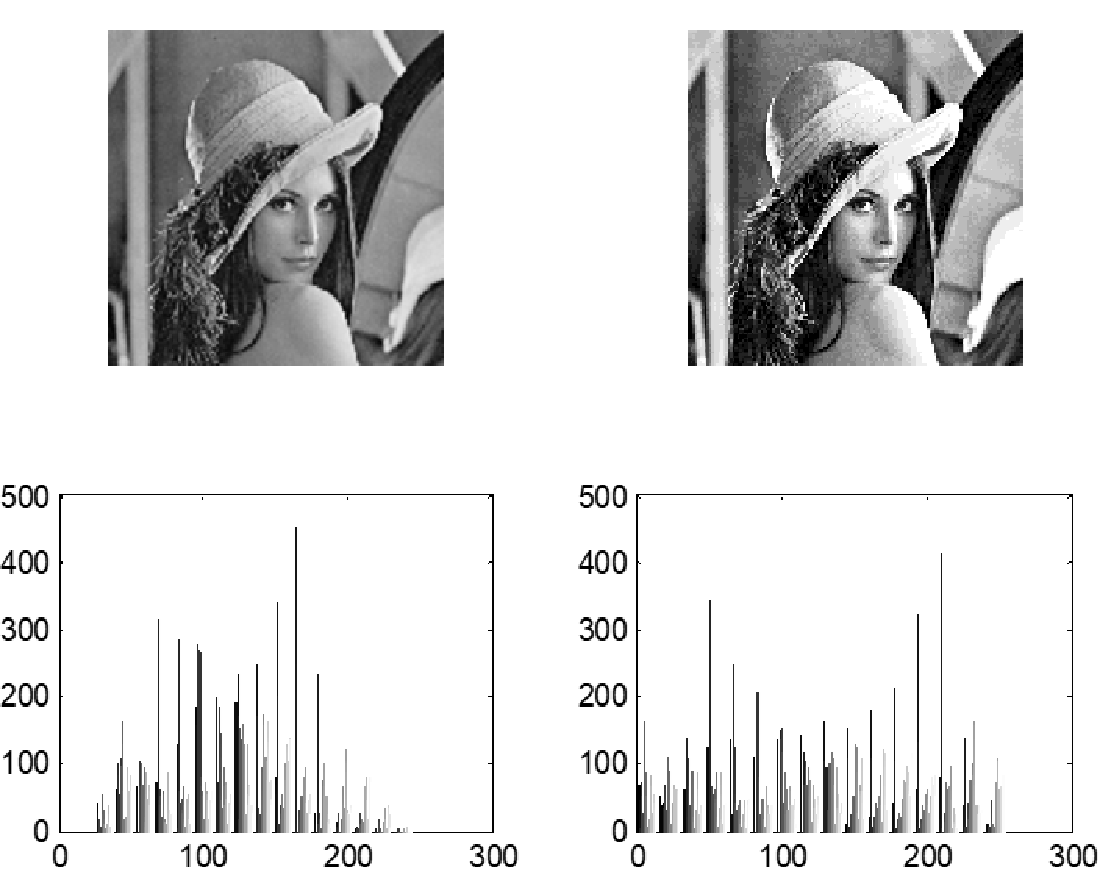
变换后直方图 趋向平坦,灰度级减少,灰度合并。
原始图像 含有像素数多的几个灰度级间隔被拉大 了。
压缩的只是像素数少的几个灰度级,实际视觉能够接受的信息量大大增强了。
2.2.3 直方图规定化
将 输入图像灰度分布 变换成一个 期望的灰度分布直方图。
\(p_r(r)\) 为原图的灰度密度函数, \(p_z(z)\) 为期望得到的灰度密度函数。
基本步骤如下:
-
分别对 \(p_r(r)\)、 \(p_z(z)\) 作直方图均衡化处理
\[s = T(r) = (L - 1)\int_0^rp_r(r) \text{d}r \]\[v = G(z) = (L - 1)\int_0^rp_z(z)\text{d}z \]期望变换后的灰度 \(s\) 和 \(v\) 具有相同的密度函数
-
找出 \(s\) 和 \(v\) 的对应关系(单映射 或 组映射),一般选择较近的
\[s \Leftrightarrow v \] -
确定 \(r\) 到 \(z\) 的变换关系
\[r \rightarrow s \Leftrightarrow v \rightarrow z \]
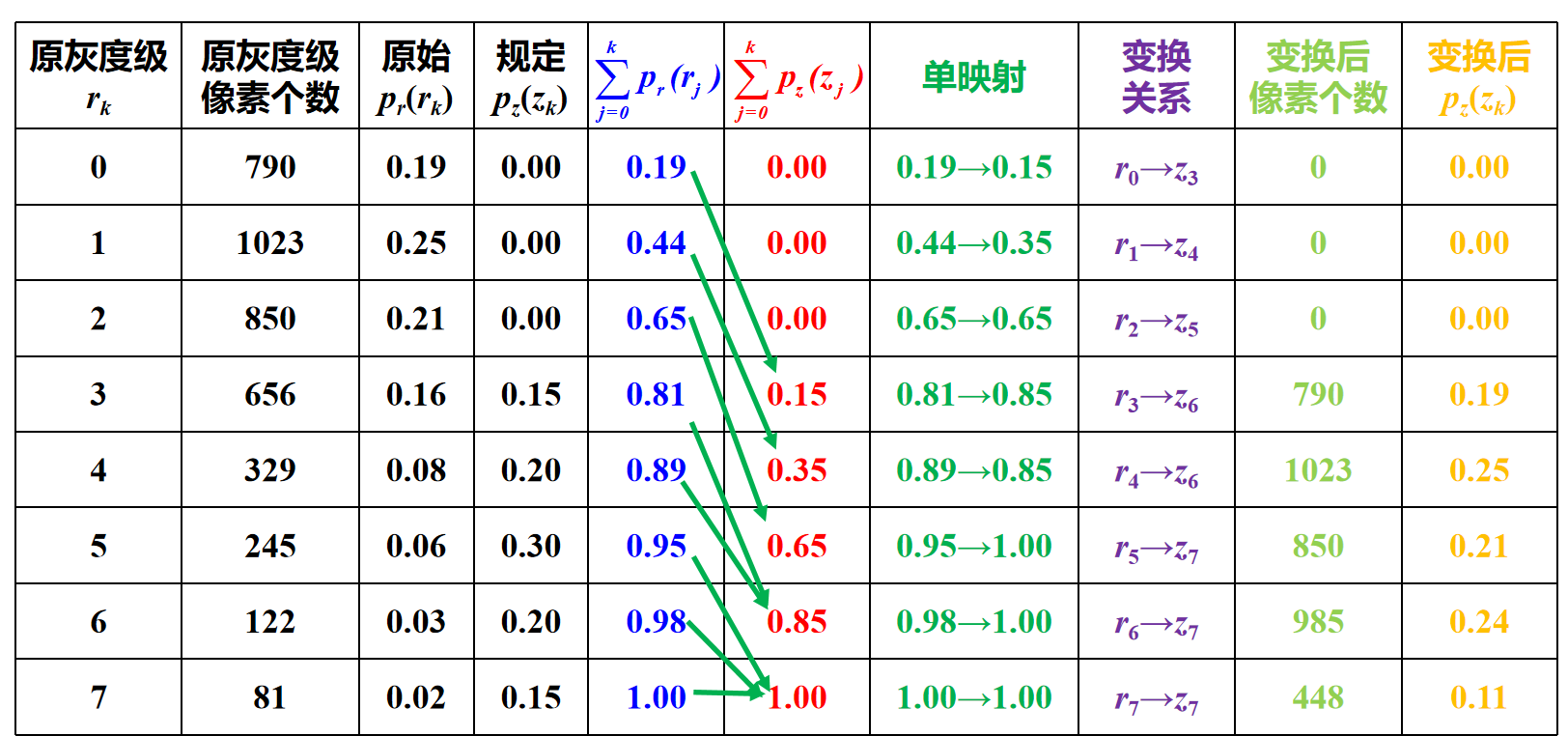
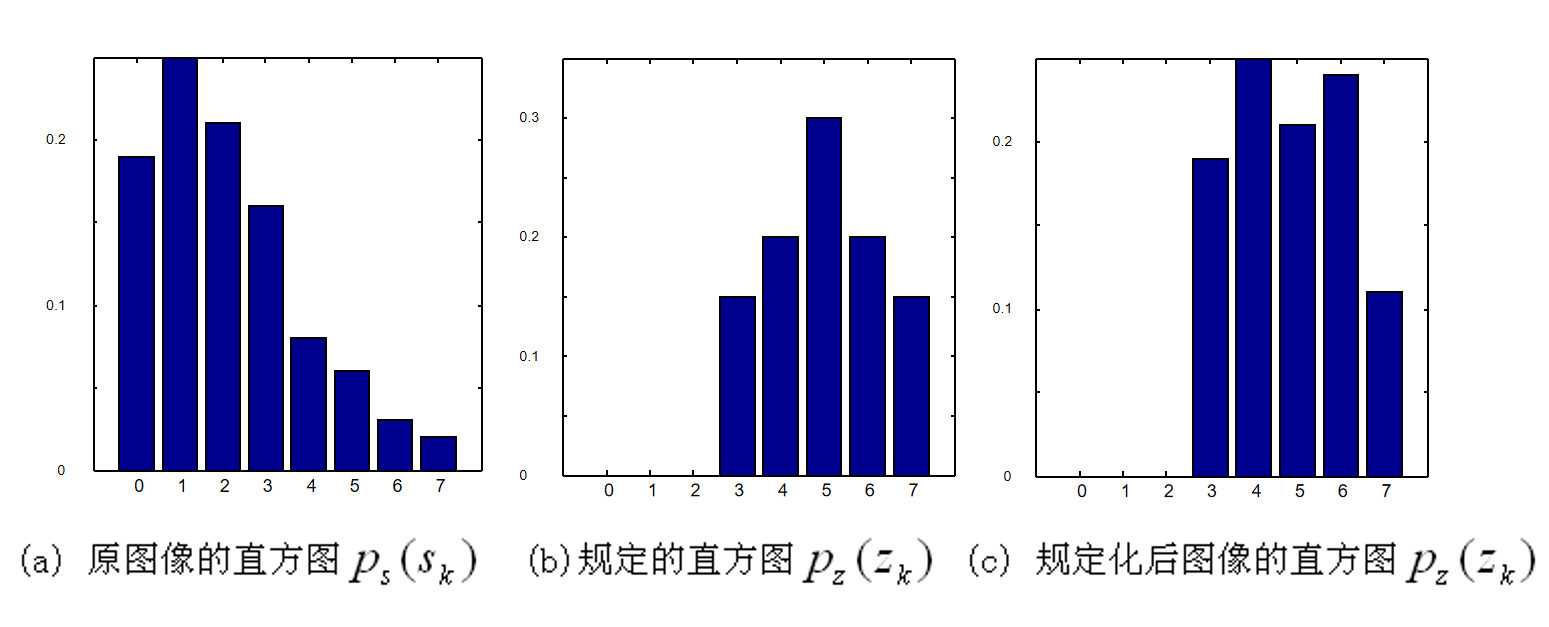
下表为书上的示例:
一幅64×64像素的图像,灰度级数为8
2.3 空间域滤波
2.3.1 空间域滤波概念
空间域滤波增强采用 模板处理方法 对图像进行滤波,去除图像噪声或增强图像的细节。
最常用的模板是一个小的 \(3×3\) 二维阵列,模板的系数值决定了处理的性质,如 图像平滑 或 锐化 等。
2.3.2 空间域平滑滤波器
-
局部平滑法
局部平滑处理算法很简单,但是在降低噪声的同时也使图像变得模糊了,特别在图像的边缘和细节处。
一般采用领域均值法进行滤波。
邻域越大,在 去噪能力增强 的同时 模糊程度越严重。

相关代码:
I = imread('4.png'); I = im2double(I); subplot(1,3,1); imshow(I); title('Original Image'); I_noised = imnoise(I, 'salt & pepper', 0.05); subplot(1,3,2); imshow(I_noised); title('Image after noised'); I_filtered = imfilter(I_noised, fspecial('average', 5)); subplot(1,3,3); imshow(I_filtered); title('Image after Local Smoothing'); -
超限像素平滑法
超限像素平滑法是对领域均值法的改进。
将 \(f(x, y)\) 和邻域平均 \(g(x, y)\) 的差的绝对值与选定的阈值进行比较,根据比较结果确定点 \((x, y)\) 最后的灰度 \(h(x, y)\)
\[h(x, y) = \begin{cases} g(x, y), \; |f(x, y) - g(x, y)| > T \\ f(x, y), \; |f(x, y) - g(x, y)| \le T \end{cases} \]这种算法对保护仅有微小灰度差的细节及纹理也有效。
同样的,邻域越大,在 去噪能力增强 的同时 模糊程度越严重。
-
灰度K近邻平均法
在 \(n×n\) 的窗口内,属于同一集合体的像素,它们的灰度值将高度相关。
可用窗口内与中心像素的灰度 最接近的 \(K\) 个邻点像素 的 平均灰度 来代替窗口中心像素的灰度值。
较小的 \(K\) 值使噪声方差下降较小,但保持细节效果较好:而较大的 \(K\) 值平滑噪声较好,但会使图像边缘模糊。
-
空间低通滤波法
根据问题选取合适的 滤波器。
滤波器的权值之和必须为1,由此可以保证输出图像的灰度值在灰度范围内,不会 出现 溢出。
2.3.3 空间域锐化滤波器
图像锐化就是 增强图像的边缘或轮廓。
图像平滑通过积分过程使得图像边缘模糊。图像锐化则 通过微分 而使图像 边缘突出、清晰。
-
梯度锐化法
对于图像 \((x, y)\),在 \((x, y)\) 处的梯度为:
\[\text{grad}(x, y) = \begin{bmatrix} f_x^{'} \\\\ f_y^{'} \end{bmatrix} = \begin{bmatrix} \frac{\partial f(x, y)}{\partial x} \\\\ \frac{\partial f(x, y)}{\partial y} \end{bmatrix} \]大小和方向为:
\[|\text{grad}(x, y)| = \sqrt{(f_x^{'})^2 + (f_y^{'})^2} \]\[\theta = \text{arctan}(\frac{f_y^{'}}{f_x^{'}}) \]对于离散图像而言,一阶偏导数采用一阶差分近似表示:
\[\begin{split} f_x^{'} = f(x + 1, y) - f(x, y) \\\\ f_y^{'} = f(x, y + 1) - f(x, y) \end{split} \]一般采用简化计算(两种形式):
\[\begin{split} & \text{grad}(x, y) = \max(|f_x^{'}|, |f_y^{'}|) \\\\ & \qquad \text{or} \\\\ & \text{grad}(x, y) = |f_x^{'}| + |f_y^{'}| \end{split} \]如图所示:

相关代码:
I = imread('4.png'); I = rgb2gray(I); I = im2double(I); % 定义水平和垂直方向上的梯度算子 hy = -fspecial('sobel'); % 水平方向 hx = hy'; % 垂直方向 % 计算水平和垂直方向上的梯度 gy = imfilter(I, hy); gx = imfilter(I, hx); % 计算梯度幅度 g = sqrt(gx.^2 + gy.^2); % 以0.02为阈值,对梯度图像进行阈值处理,得到二值图像 bw = g>0.02; subplot(221), imshow(I), title('Original Image') subplot(222), imshow(g), title('Gradient Magnitude') subplot(223), imshow(bw), title('Binary Gradient Magnitude (Thresholded at 0.02)') subplot(224), imshow(bw.*I), title('Enhanced Edges') -
拉普拉斯算子
有如下定义:
\[\begin{split} & \nabla^2 f = \frac{\partial ^2 f}{\partial x^2} + \frac{\partial ^2 f}{\partial y^2} \\\\ & \nabla^2 f = \Delta_x^2f(x, y) + \Delta_y^2f(x, y) \\\\ & \Delta_x^2f(x, y) = f(x + 1, y) + f(x - 1, y) - 2f(x, y) \\\\ & \Delta_y^2f(x, y) = f(x, y + 1) + f(x, y - 1) - 2f(x, y) \\\\ & \nabla^2 f = f(x + 1, y) + f(x - 1, y) + f(x, y + 1) + f(x, y - 1) - 4 f(x, y) \end{split} \]相当于用如下滤波器进行卷积:
\[\begin{bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{bmatrix} \] -
低频分量消减法
-
从原始图像中减去 平滑低频图像 \(\bar f(x, y)\),得到输出图像 \(g(x, y)\)
\[g(x, y) = f(x, y) - \bar f(x, y) \] -
对原图像进行加权,减去低通成分
\[g(x, y) = Kf(x, y) - f_{Lp}(x, y) \] -
2.4 频率域滤波
2.4.1 频率域滤波概念
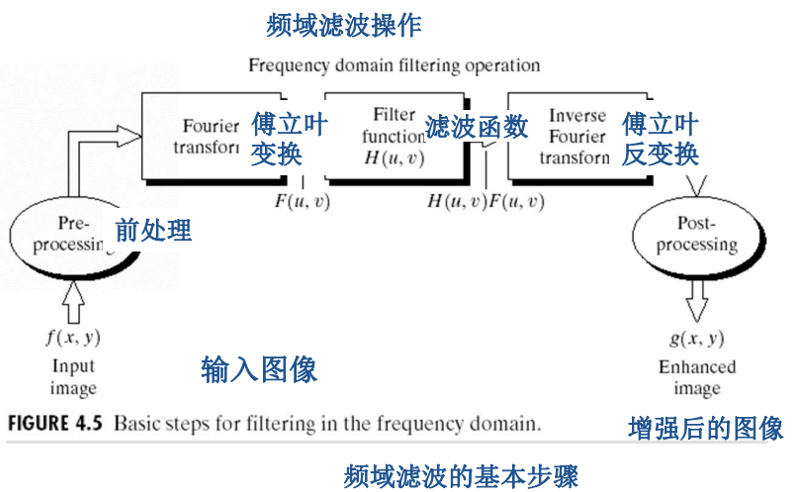
图像空间域的线性领域卷积相当于图像经过滤波器对图像信号频率成分成分的滤波。
关键在于 设计频域滤波器的传递率函数 \(H(u, v)\)
2.4.2 频域率平滑滤波器
- 理想低通滤波器
假设傅里叶平面上理想低通滤波器离开原点的 截至频率 为 \(D_0\),有如下传递函数:
输入信号在通带内所有频率分量完全无损地通过,而在阻带内所有频率分量完全衰减。
该方法有陡峭频率的截止特性,但会产生振铃现象使图像变得模糊,该滤波器具有物理不可实现性。
- 巴特沃斯低通滤波器
\(n\) 阶 \(\text{Butterworth}\) 低通滤波器的传递函数:
其中 \(D_0\) 为截止频率。
传递函数 比较平滑,连续性衰减,不像理想滤波器那样陡峭变化。
采用该滤波器滤波在 抑制噪声 的同时,图像边缘的 模糊程度大大减小 。
一阶没有振铃,二阶则稍有感受但几乎没有,而在高阶则可明显地感受到振铃的现象。
如图所示;

相关代码:
I = imread('3.png');
I = rgb2gray(I);
I = im2double(I);
subplot(1, 2, 1);
imshow(I), title('Original Image');
I1 = fftshift(fft2(I));
[M, N] = size(I1);
n = 2;
D0 = 30;
n1 = floor(M / 2);
n2 = floor(N / 2);
I2 = zeros(M, N);
for i=1:M
for j=1:N
D = sqrt((i - n1) ^ 2 + (j - n2) ^ 2);
H = 1 / (1 + (D / D0) ^ (2 * n));
I2(i, j) = H * I1(i, j);
end
end
I3 = real(ifft2(ifftshift(I2)));
subplot(1, 2, 2);
imshow(I3), title('filtered Image');
- 指数低通滤波器
图像边缘的模糊程度比巴特沃斯稍微大一些,无明显的振铃效应。
- 梯形低通滤波器
性能介于低通滤波器和指数滤波器之间,有一定模糊和振铃效应。
2.4.3 频域率锐化滤波器
图像的边缘、细节主要位于高频部分,图像的模糊主要由于高频成分比较弱导致的。
频域率锐化是为了 消除模糊、突出边缘。
采用高频滤波器让高频成分通过,使得低频成分削弱,在经过傅里叶逆变换得到边缘锐化的图像。
- 理想高通滤波器
- 巴特沃斯高通滤波器
如图所示:

相关代码:
I = imread('3.png');
I = rgb2gray(I);
I = im2double(I);
subplot(1, 2, 1);
imshow(I), title('Original Image');
I1 = fftshift(fft2(I));
[M, N] = size(I1);
n = 2;
D0 = 30;
n1 = floor(M / 2);
n2 = floor(N / 2);
I2 = zeros(M, N);
for i=1:M
for j=1:N
D = sqrt((i - n1) ^ 2 + (j - n2) ^ 2);
H = 1 / (1 + (D0 / D) ^ (2 * n));
I2(i, j) = H * I1(i, j);
end
end
I3 = real(ifft2(ifftshift(I2)));
subplot(1, 2, 2);
imshow(I3), title('filtered Image');
- 指数高通滤波器
- 梯形高通滤波器
2.4.4 同态滤波器
真实的图像除了有加性噪声外,往往还存在乘性或卷积性噪声。此时,直接用频域滤波的方法,将无法消减乘性或卷积性噪声。
同态滤波 基本思想是 将非线性问题转化成线性问题 处理。
即先对非线性混杂信号作某种数学运算,变换成相加的两个分量,然后用线性滤波方法处理,最后作逆运算,恢复处理后图像。
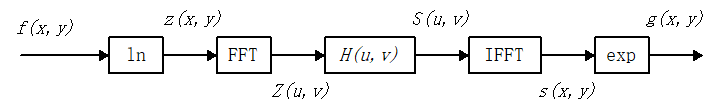
一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MarisaMagic/p/17895929.html,未经允许严禁转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号