[数字图像处理笔记] 第三章 图像基本运算

1. 基本运算概述

  • 点运算

    指对一幅图像中每个像素点的灰度值按照一定的映射关系进行计算的方法。

  • 代数运算、逻辑运算

    指将两幅或多幅图像通过对应像素之间的 加、减、乘、除、逻辑 与、或、非 等运算得到输出图像的方法。

  • 几何运算

    指改变图像中物体对象 (像素) 之间的空间关系，进行图像的 平移、镜像、旋转、缩放 以及 复合变换。


2. 点运算

2.1 线性点运算

线性点运算的灰度变换函数可以采用线性方程描述：

\[s = ar + b \]

其中，\(r\) 为输入的灰度值，\(s\) 为对应的输出的灰度值，\(a\), \(b\) 为函数参数。

  • 当 \(a = 1\) 且 \(b = 0\) 时，图像不变；当 \(a = 1\) 但 \(b \not = 0\) 时，所有像素的灰度值会上升或下降，即 \(a=1\) 时，当 \(b > 0\) 整体所有像素的亮度会增加，反之，当 \(b < 0\) 整体所有像素的亮度会降低。

    如图所示，\(b\) 的取值分别为 0, 50, 100, 150，随着 \(b\) 增大，图像的亮度也越来越高。

    相关代码如下：

    I = imread("1.png");
I = rgb2gray(I);

subplot(221);
imshow(I);
title("s = r");

I2 = I + 50;
subplot(222);
imshow(I2);
title("s = r + 50");

I3 = I + 100;
subplot(223);
imshow(I3);
title("s = r + 100");

I4 = I + 150;
subplot(224);
imshow(I4);
title("s = r + 150");

    如图所示，如图所示，\(b\) 的取值分别为 0, -50, -100, -150，随着 \(b\) 不断减小，图像的亮度也越来越低。

    相关代码如下：

    I = imread("2.png");
I = rgb2gray(I);

subplot(221);
imshow(I);
title("s = r");

I2 = I - 50;
subplot(222);
imshow(I2);
title("s = r - 50");

I3 = I - 100;
subplot(223);
imshow(I3);
title("s = r - 100");

I4 = I - 150;
subplot(224);
imshow(I4);
title("s = r - 150");

  • 当 \(a > 1\) 时，图像的 对比度增大，黑白对比越明显。

    如图所示，当 \(b\)不变，\(a\) 的取值为 1, 1.5, 2, 2.5 时，随着 \(a\) 不断增大，黑白对比越来越明显。当然 \(a\) 不能过大，否则会接近全部白色。

    相关代码如下：

    I = imread("3.jpg");
I = rgb2gray(I);

subplot(221);
imshow(I);
title("s = r");

I2 = 1.5 .* I;
subplot(222);
imshow(I2);
title("s = 1.5 * r");

I3 = 2 .* I;
subplot(223);
imshow(I3);
title("s = 2 * r");

I4 = 2.5 .* I;
subplot(224);
imshow(I4);
title("s = 2.5 * r");

  • 当 \(a < 1\) 时，图像的 对比度降低。

    如图所示，当 \(b\)不变，\(a\) 的取值为 1, 0.8, 0.5, 0.2 时，随着 \(a\) 不断减小。当然 \(a\) 不能过小，否则会接近全部黑色。

    相关代码如下：

    I = imread("3.jpg");
I = rgb2gray(I);

subplot(221);
imshow(I);
title("s = r");

I2 = 0.8 .* I;
subplot(222);
imshow(I2);
title("s = 0.8 * r");

I3 = 0.5 .* I;
subplot(223);
imshow(I3);
title("s = 0.5 * r");

I4 = 0.2 .* I;
subplot(224);
imshow(I4);
title("s = 0.2 * r");

  • 当 \(a < 0\) 时，则 暗区变亮，亮区变暗，完成了图像求补。

    如图所示，当 \(a = -1, b = 255\) 时，求得原图的补，即图像反色。

    \(b = 0\) 时，当 \(a<0\) ，其灰度值会变为负数，而灰度值的范围是 \([0，255]\)，故会取最小值0，因此，当a取值为负时，所运算后的结果会显示为一幅全黑图片。

    相关代码如下：

    I = imread("4.png");
I = rgb2gray(I);

subplot(121);
imshow(I);
title("s = r");

I2 = -double(I) + 255;
subplot(122);
imshow(I2);
title("s = -1 * r + 255");

2.2 非线性点运算

非线性点运算的输出灰度级与输入灰度级呈非线性关系，常见的非线性变换为 对数变换 和 幂次变换 。

2.2.1 对数变换

一般有表达式：

\[s = c \;\text{log}_2(1 + r) \]

其中 \(c\) 是常数，\(r \ge 0\)

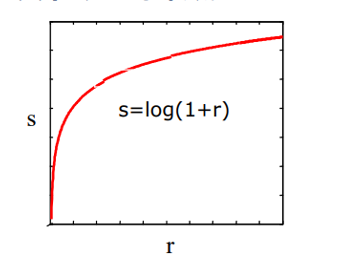
对数变换 扩展图像的低灰度级，压缩图像的高灰度级，起到了 图像加亮、减暗 的效果。

如图所示

相关代码：

I = imread("5.png");
I = rgb2gray(I);

subplot(121);
imshow(I);
title("s = r");

I2 = 1.5 * log(1 + im2double(I));
subplot(122);
imshow(I2);
title("s = c * log(1 + r)");

2.2.2 幂次变换

幂次变换一般有如下形式：

\[s = c\;r^\gamma \]

其中，一般 \(c > 0\), \(\gamma > 0\) 的常数

  • 当 \(\gamma > 1\) 时，变化曲线在线性函数之上，此时 拓展 图像的 高灰度级，压缩低灰度级

  • 当 \(0 < \gamma < 1\) 时，变化曲线位于线性函数下方，此时 拓展 图像的 低灰度级，压缩图像高灰度级。

  • 当 \(\gamma = 1\) 此时退化为线性点运算。

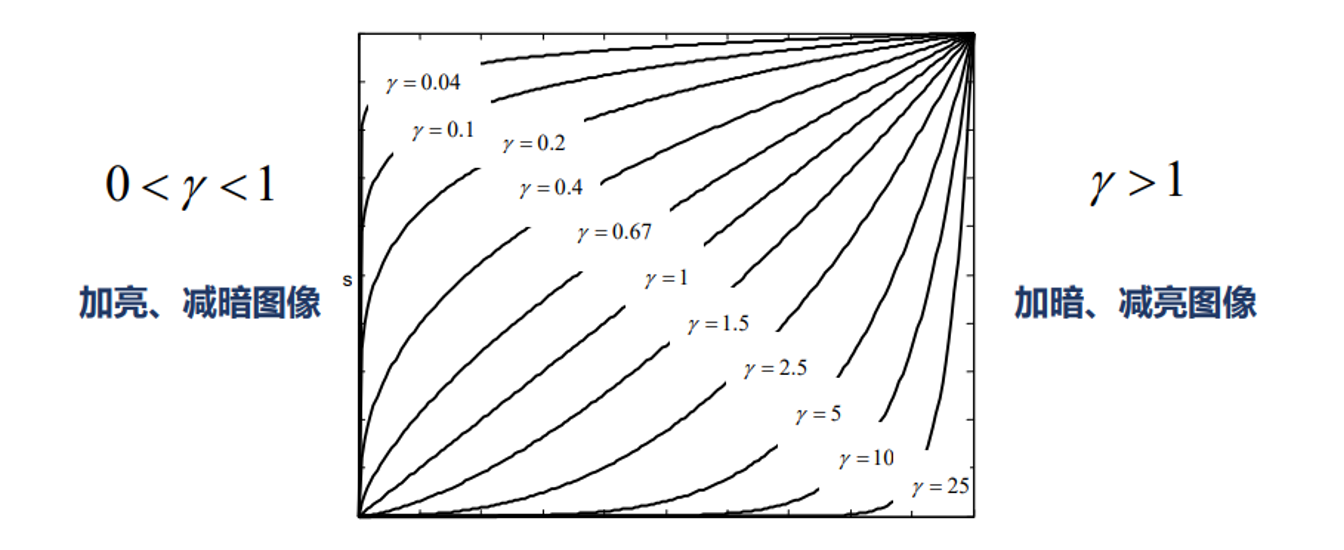
如下图所示，为 \(\gamma = 2\) 时的图像，此时 加暗、减亮

相关代码如下：

I = imread("5.png");
I = rgb2gray(I);
I = im2double(I);

subplot(121);
imshow(I);
title("s = r");

I2 = I .^ 2;
subplot(122);
imshow(I2);
title("s = c * r ^ 2");

如下图所示，为 \(\gamma = 0.5\) 时的图像，此时 加亮、减暗

相关代码如下：

I = imread("5.png");
I = rgb2gray(I);
I = im2double(I);

subplot(121);
imshow(I);
title("s = r");

I2 = I .^ 0.5;
subplot(122);
imshow(I2);
title("s = c * r ^ 0.5");

3. 代数运算与逻辑运算

3.1 加法运算

一般有如下形式：

\[C(x,y) = A(x, y) + B(x, y) \]

其中 \(C(x, y)\) 为输出图像，\(A(x, y)\) 和 \(B(x, y)\) 为输入图像。

假设噪声图像集 \({g_i(x, y)}, \; i = 1, 2, ... , M\)

\[g_i(x, y) = f_i(x, y) + e_i(x, y) \]

由此可得 \(M\) 个图像的均值：

\[\bar g(x, y) = \frac{1}{M} \sum_{i = 1}^M[f_i(x, y) + e_i(x, y)] = f(x, y) + \frac{1}{M}\sum_{i=1}^Me_i(x, y) \]

当噪声 \(e_i(x, y)\) 互不相关，且均值为0时，图像均值将降低噪声的影响。

如图所示，分别为原始图像，加入噪声后的图像，以及平均图像：

相关代码如下：

I = imread("1.png");
I = rgb2gray(I);

subplot(131);
imshow(I);
title("initial img");

I2 = imnoise(I, 'gaussian', 0, 0.02);
subplot(132);
imshow(I2);
title("noised img");

[M, N] = size(I);
S = zeros(M, N);

for i=1:100
    J = imnoise(I, 'gaussian', 0, 0.02);
    J = im2double(J);
    S = S + J;
end

S = S / 100;
subplot(133);
imshow(S);
title("average img");

通过加法运算，可以得到图像合成的效果，形成两幅或多福图像的衔接(注意相加要保证两幅图像大小一致)：

相关代码如下：

I1 = imread("1.png");
I1 = im2double(I1);
subplot(131);
imshow(I1);
title("img1");

[M, N, K] = size(I1);

I2 = imread("6.jpg");
I2 = imresize(I2, [M, N]);
I2 = im2double(I2);
subplot(132);
imshow(I2);
title("img2");

I3 = 0.7 * I1 + 0.3 * I2;
subplot(133);
imshow(I3, []);
title("img3");

3.2 减法运算

一般有如下表达式：

\[C(x, y) = A(x, y) - B(x, y) \]

将同一景物在不同时间拍摄的图像相减，即图像的减法运算，实际中称为 差影法。

假设 \(t_1\) 时刻图像为 \(T_1(x, y)\); \(t_2\) 时刻图像为 \(T_2(x, y)\)，则同一场景内，两幅图像之间的变化为：

\[g(x, y) = T_2(x, y) - T_1(x, y) \]

如图所示，通过减法运算，可以提取出之前添加的噪声图像：

相关代码如下：

I1 = imread("1.png");
subplot(131);
imshow(I1);
title("img1");

I2 = imnoise(I1, 'salt & pepper', 0.1);
subplot(132);
imshow(I2);
title("img2");

I3 = imsubtract(I2, I1);
subplot(133);
imshow(I3);
title("img3");

3.3 乘法运算

一般有如下形式：

\[C(x, y) = A(x, y) \times B(x, y) \]

简单的乘法运算可以用来改变图像的灰度级，实现灰度级变换。

乘法运算有时也被用于卷积和相关处理。

如图所示：

相关代码如下：

I1 = imread("2.png");
I1 = rgb2gray(I1);
subplot(131);
imshow(I1);
title("img");

I2 = immultiply(I1, 1.5);
subplot(132);
imshow(I2);
title("img x 1.5");

I3 = immultiply(I1, 0.5);
subplot(133);
imshow(I3);
title("img x 0.5");

3.4 除法运算

一般有如下形式：

\[C(x, y) = A(x, y) / B(x, y) \]

除法运算也可以改变图像的灰度级，常用于遥感图像处理中。是非常重要的图像增强处理运算。

相关代码：

img1 = imread('1.png');
img2 = imread('2.png');

img1 = im2double(img1);
img2 = im2double(img2);

subplot(131);
imshow(img1);

[M, N, K] = size(img1);
img2 = imresize(img2, [M, N]);

subplot(132);
imshow(img2);

imgDivide = imdivide(img1, img2);
imgDivide = im2uint8(imgDivide);
subplot(133);
imshow(imgDivide);

3.5 逻辑运算

逻辑运算是将 两幅或多幅图像 通过对应的像素之间的 与、或、非 逻辑运算得到输出图像的方法。

相关代码如下：

A = zeros(128);
A(40:70, 60:100) = 1;
subplot(231);
imshow(A);
title("A");

B = zeros(128);
B(60:90, 30:70) = 1;
subplot(232);
imshow(B);
title("B");

C = and(A, B);
subplot(233);
imshow(C);
title("A & B");

D = or(A, B);
subplot(234);
imshow(D);
title("A | B");

E = xor(A, B);
subplot(235);
imshow(E);
title("A ^ B");

F = not(A);
subplot(236);
imshow(F);
title("!A");

4. 几何运算

4.1 平移

像素点的平移如图所示：

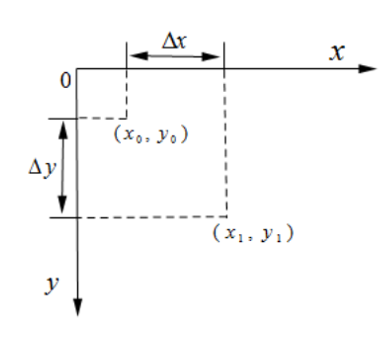
由此可以得出两个像素点之间的坐标关系：

\[\begin{cases} x_1 = x_0 + \Delta x \\ y_1 = y_0 + \Delta y \end{cases} \]

其矩阵表示如下：

\[\begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & \Delta x \\ 0 & 1 & \Delta y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} \]

如图所示，图像完成了平移：

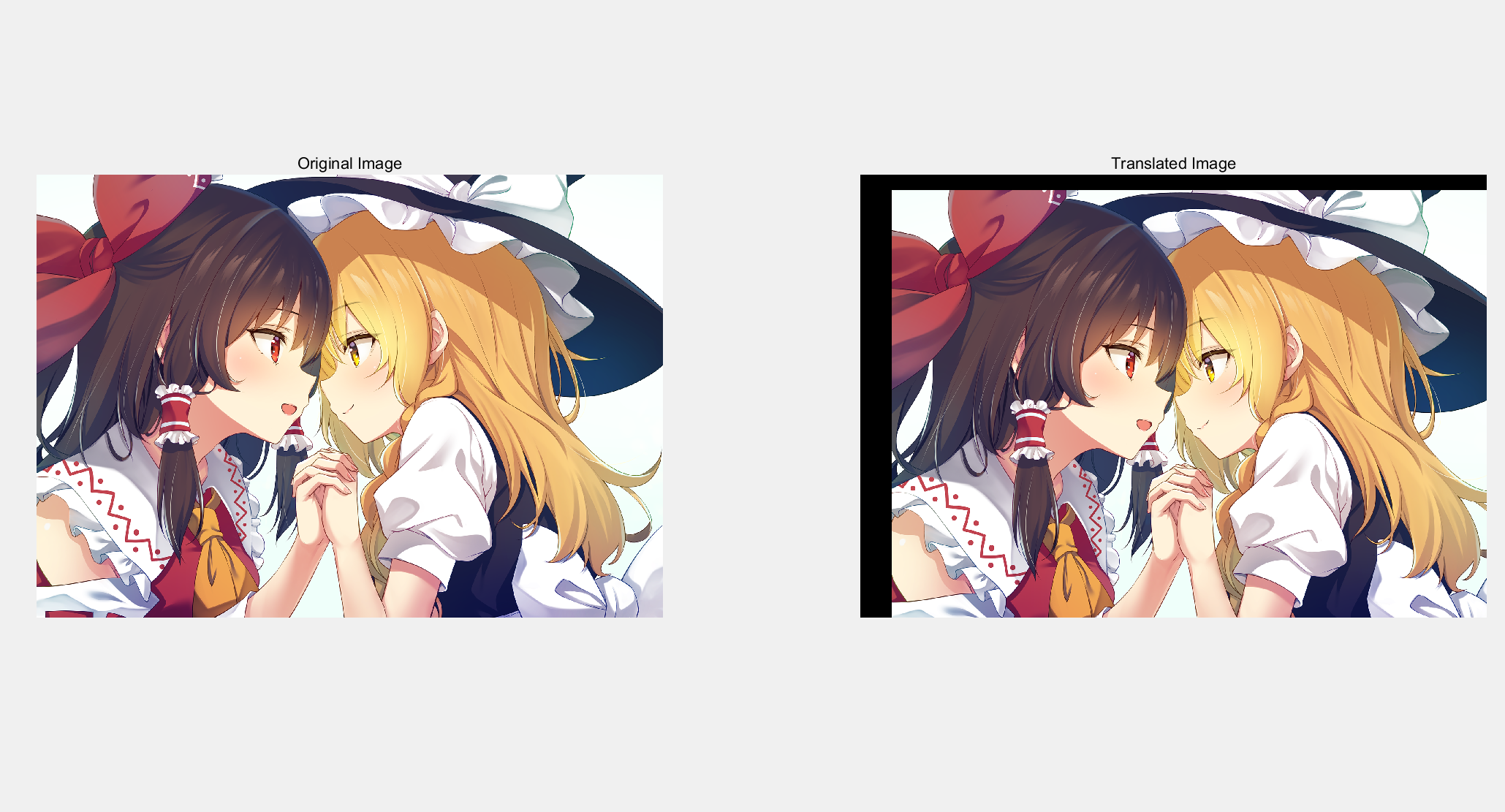
相关代码如下：

img = imread('4.png');

translation = [100, 50]; 

img_translated = imtranslate(img, translation, 'FillValues', 0);

subplot(1, 2, 1);
imshow(img);
title('Original Image');
subplot(1, 2, 2);
imshow(img_translated);
title('Translated Image');

4.2 镜像

4.2.1 水平镜像

水平镜像 以垂直中心轴 为中心，水平镜像的变换公式：

\[\begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} = \begin{bmatrix} -1 & 0 & n \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} \]

如图所示：

相关代码如下：

img = imread('3.jpg');
subplot(121);
imshow(img);
title('Original Image');

img_mirror = fliplr(img);
subplot(122);
imshow(img_mirror);
title('Mirror Image');

4.2.2 垂直镜像

垂直镜像 以水平中心轴 为中心，垂直镜像的变换公式：

\[\begin{bmatrix} x_1 \\ y_1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & m \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} \]

如图所示：

相关代码如下：

img = imread('3.jpg');
subplot(121);
imshow(img);
title('Original Image');

img_mirror = flipud(img);
subplot(122);
imshow(img_mirror);
title('Mirror Image');

4.3 旋转

由笛卡尔坐标系，可以得到原始图像上的点坐标为：

\[\begin{cases} x_0 = r\;\text{cos}\alpha \\ y_0 = r\;\text{sin}\alpha \end{cases} \]

旋转 \(\beta\) 角度之后的点坐标：

\[\begin{cases} x = r \; \text{cos}(\alpha - \beta) = r \; \text{cos}\alpha \; \text{cos}\beta + r \; \text{sin}\alpha \; \text{sin}\beta \\ y = r \; \text{sin}\alpha \; \text{cos}\beta - r \; \text{cos}\alpha \; \text{sin}\beta \end{cases} \]

化简可得：

\[\begin{cases} x = x_0 \; \text{cos}\beta + y_0 \; \text{sin}\beta \\ y = -x_0 \; \text{sin}\beta + y_0 \; \text{sin}\beta \end{cases} \]

其矩阵表示如下：

\[\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} \text{cos}\beta & \text{sin}\beta & 0 \\ -\text{sin}\beta & \text{cos}\beta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} \]

如图所示，图像进行了旋转：

相关代码如下：

img = imread('3.jpg');
subplot(1, 2, 1);
imshow(img);
title('Original Image');

angle = 45; 

img_rotated = imrotate(img, angle, 'bilinear', 'crop');
subplot(1, 2, 2);
imshow(img_rotated);
title('Rotated Image');

4.4 缩放

数字图像的全比例缩放是指将给定的图像在 \(x\) 方向和 \(y\) 方向按相同的比例 \(\alpha\) 缩放，从而获得一幅新的图像。

\[\begin{cases} x_1 = \alpha x_0 \\ y_1 = \alpha y_0 \end{cases} \]

其矩阵表述：

\[\begin{cases} x = x_0 \; \text{cos}\beta + y_0 \; \text{sin}\beta \\ y = -x_0 \; \text{sin}\beta + y_0 \; \text{sin}\beta \end{cases} \]

其矩阵表示如下：

\[\begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & 0 \\ 0 & \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_0 \\ y_0 \\ 1 \end{bmatrix} \]

如图所示，图像进行了放大和缩小：

相关代码如下：

img = imread('3.jpg');
img = rgb2gray(img);
img_resized = imresize(img, [700, 700]);
figure(1);
imshow(img_resized);
title('Resized Image');

img_resized = imresize(img, [200, 200]);
figure(2);
imshow(img_resized);
title('Resized Image');

4.5 灰度重采样

如果一个输出的像素映射到四个输入像素之间，则其灰度值由 灰度插值算法 决定。

  • 最近邻法

  • 双线性插值法

  • 三次内插法

如图所示，分别为原始图像以及三种算法处理后的图像。

可以看出，最近邻法的效果最模糊，三次内插法的效果最好。

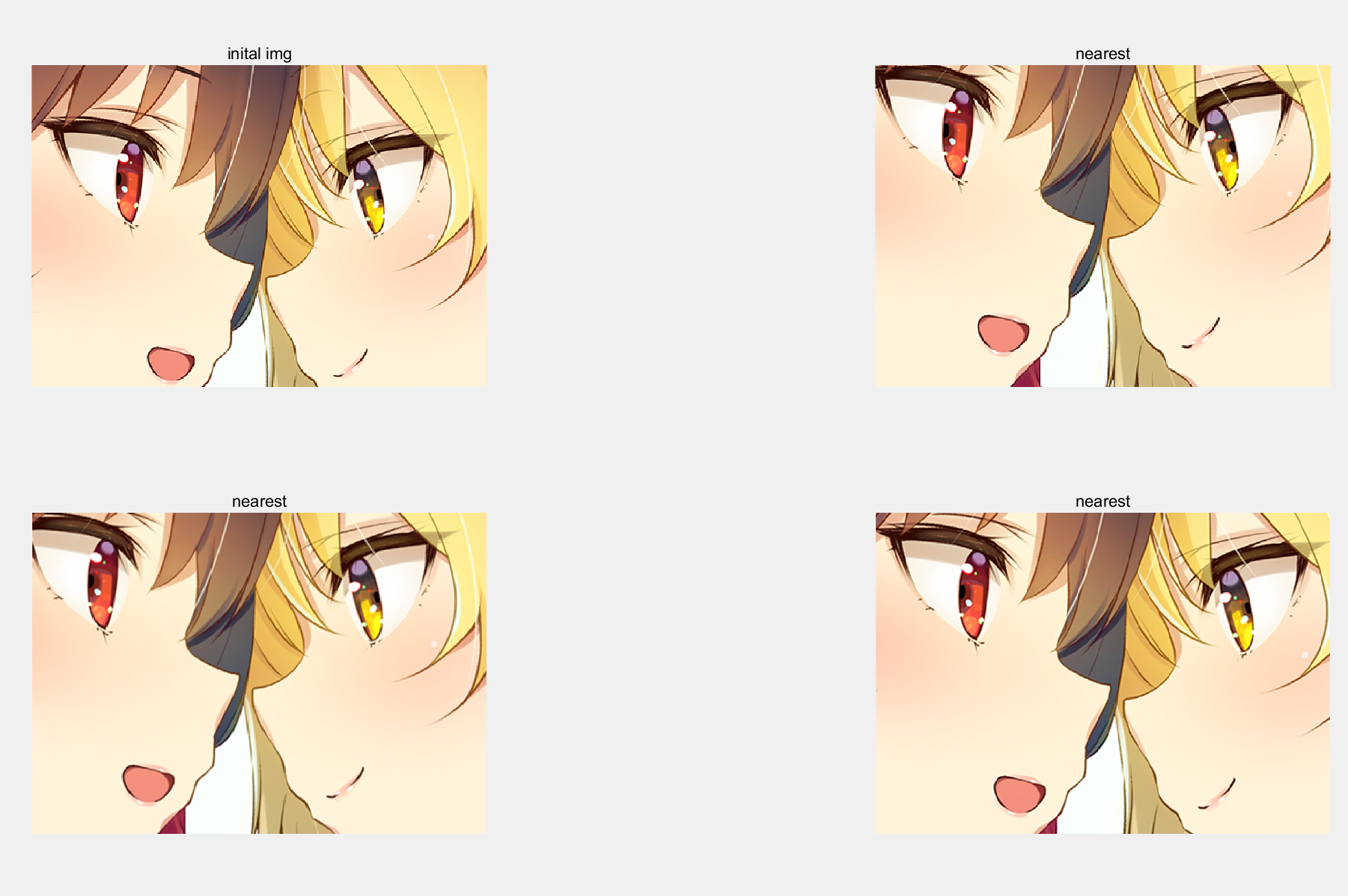
相关代码如下：

I = imread('4.png');

subplot(221);
imshow(I);
title('inital img');

I2 = imresize(I, 10, 'nearest');
subplot(222);
imshow(I2);
title('nearest');

I3 = imresize(I, 10, 'bilinear');
subplot(223);
imshow(I3);
title('nearest');

I4 = imresize(I, 10, 'bicubic');
subplot(224);
imshow(I4);
title('nearest');

PS：后来发现这里图像的标题写错了，后面两个图对应的是 "bilinear", "bicubic"

posted @ 2023-12-11 00:03  MarisaMagic  阅读(981)  评论(1)  编辑  收藏  举报