[机器学习复习笔记] KNN（k近邻）

KNN

1. KNN 算法 （\(k\) 近邻）

\(k\) 近邻学习 (\(\text{k-nearest} \; \text{neighbor}, \; k\text{-NN}\)) 是一种常用的监督学习方法，思路非常简单：给定一个样本数据集，对于每个输入的测试样本，在训练集中找到与该测试样本 最近的 \(k\) 个 训练样本，然后基于这 \(k\) 个样本的类别标记，通过 投票法 选出 出现最多的类别标记 作为当前测试样本的预测结果。

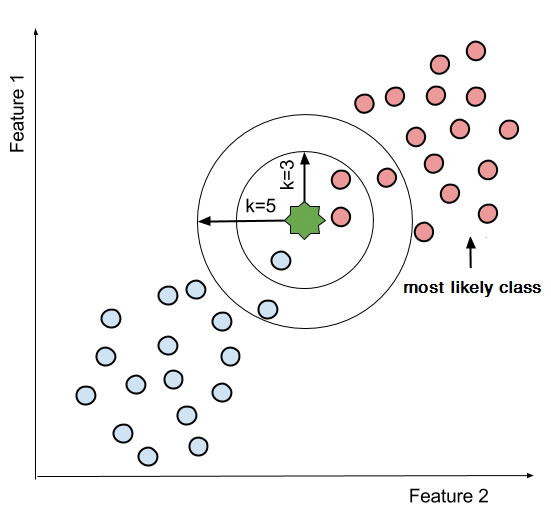
\(\text{KNN}\) 算法形式化表述如下：

输入训练集 \(D = \{(x_1, y_1), (x_2, y_2), ... , (x_n, y_n)\}\)，其中 \(x_i\) 为 \(d\) 维特征向量，\(y_i\) 为每个训练样本标记的类别，\(y_i \in \{c_1, c_2, ... , c_t\}\)，共 \(t\) 个类别。

1. 根据 指定的距离度量方法，在训练集 \(D\) 中找出与当前测试样本 \(x\) 最近邻的 \(k\) 个点，涵盖这 \(k\) 个点的邻域记作 \(N_k(x)\)

2. 在邻域 \(N_k(x)\) 中，采用 投票法 找出出现次数最多的类别，以此来决定 \(x\) 的类别 \(y\)。其中 \(I\) 为 指示函数，当 \(y_i = c_j\) 时为 \(1\)，否则为 \(0\)。

   \[y = \text{arg} \; \max_{c_j} \sum_{x_i \in N_k(x)} I(y_i = c_j), \quad i = \{1, 2, ... , n\}, \; j = \{1, 2, ... , t\} \]

事实上，\(k\) 近邻学习 没有显示的学习过程，是 懒惰学习 (\(\text{lazy} \; \text{learning}\)) 的代表。

2. 距离度量

• 闵可夫斯基距离

  \[\text{dist}_{\text{mk}}(\mathbf x_i, \mathbf x_j) = (\sum_{u = 1}^{d}|x_{iu} - x_{ju}|^p)^{\frac{1}{p}} \]

• 欧几里得距离
  当 \(p\) 取2时，闵可夫斯基距离即为欧几里得距离

  \[\text{dist}_{\text{ed}}(\mathbf x_i, \mathbf x_j) = \sqrt{\sum_{u = 1}^{d}|x_{iu} - x_{ju}|^2} \]

• 曼哈顿距离
  当 \(p\) 取1时，闵可夫斯基距离即为曼哈顿距离

  \[\text{dist}_{\text{man}}(\mathbf x_i, \mathbf x_j) = ||\mathbf x_i - \mathbf x_j||_1 = \sum_{u = 1}^{d}|x_{iu} - x_{ju}| \]

3. \(k\) 值的选择

如果选择 较小 的 \(k\) 值，相当于在较小的邻域内进行预测，学习的 近似误差 会减小，只有与输入样本足够近的训练样本才会对预测结果起作用。但是，估计误差 会增大，预测结果对近邻的样本点非常敏感。

如果选择 较大 的 \(k\) 值，相当于在较大的邻域内进行预测，可以减小 估计误差，但是，会导致 近似误差 增大，与输入样本较远的训练样本也会对预测结果起作用，反而造成了预测结果的错误。

在实际应用中，一般会取较小的 \(k\) 值，通过 交叉验证 优化 $k 值。

4. 分类决策规则

\(k\) 近邻的分类决策规则一般是 多数表决 规则。

如果分类的损失函数为 0-1 损失函数，分类函数为：

\[f: \mathbb{R}^n \rightarrow \{c_1, c_2, ... , c_t\} \]

那么 误分类率 是：

\[P(Y \ne f(X)) = 1 - P(Y = f(X)) \]

对给定的实例 \(x \in \chi\)，其 \(k\) 近邻的训练样本构成的邻域 \(N_k(x)\)，若涵盖 \(N_k(x)\) 的类别是 \(c_j\)，那么 误分类率 为：

\[\frac{1}{k}\sum_{x_i \in N_k(x)} I(y_i \ne c_j) = 1 - \frac{1}{k}\sum_{x_i \in N_k(x)}I(y_i = c_j) \]

要使 误分类率 最小，需要使 \(\sum_{x_i \in N_k(x)} I(y_i = c_j)\) 最大。

因此，多数表决规则 恰可以使得 误分类率 最小化。

5. sklearn KNN 简单调用

from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

X, y = ...

knn = KNeighborsClassifier(n_neighbors=k, metric='minkowski')

# 训练
knn.fit(X_train, y_train)

# 传入测试集查看效果
knn.score(X_test, y_test)

# 预测结果
y_pred = knn.predict(X_test)
print("predict: ", y_pred)

# 得分
acc = accuracy_score(y_test, y_pred)
print("accuracy score: ", acc)

参考

《机器学习方法》李航

《机器学习》周志华

一文掌握KNN（K-近邻算法，理论＋实例）

Python—KNN分类算法（详解）

完结篇|一文搞懂k近邻（k-NN）算法（二）