岭回归、LASSO回归
1. 岭回归
1.1 岭回归 L2正则化
在之前的 中,使用 最小二乘法求解线性回归问题 时,讨论到了 \(X^TX\) 是否可逆。
最小二乘法得到的解析解为:
\[\theta = (X^TX)^{-1}X^Ty
\]
此时只有 \(X\) 列满秩 才有解,即 \(\text{rank}(X) = \text{dim}(X)\)
有时候,数据的 特征数量 \(d\) 大于 样本数量 \(n\),此时 无法满足列满秩 ;即便满足 \(X\) 列满秩,如果 数据特征之间的相关性比较大,会使得最小二乘法求解不稳定,\(X^TX\) 的行列式接近于 \(0\)。此时就需要给 损失函数 添加一个 惩罚项 \(\frac{\lambda}{2} ||\theta||^2_2\),即 \(\frac{\lambda}{2}\sum_{j = 1}^{d}\theta_j^2\),称作 L2正则化 ( \(\lambda\) 为 正则化力度)。
此时,损失函数 及其 偏微分 如下:
\[E = \frac{1}{2}\sum_{i = 1}^{n}(y^{(i)} - f_{\theta}(x^{(i)}))^2 + \frac{\lambda}{2}\sum_{j = 1}^d\theta_j^2
\]
\[\frac{\partial E}{\partial \theta_j} = \sum^n_{i=1}(f_{\theta}(x^{(i)} - y^{(i)}))x^{(i)}_j + \lambda \theta_j
\]
可以将上面的式子 向量化表示:
\[E = \frac{1}{2}(y - X\theta)^T(y - X\theta) + \frac{\lambda}{2}\theta^T\theta
\]
其中 \(X \in \mathbb{R}^{n \times d}\), \(\theta \in \mathbb{R}^{d \times 1}\), \(y \in \mathbb{R}^{n \times 1}\).
损失函数拆开然后求偏微分:
\[\begin{split}
E & = \frac{1}{2}(y^T - \theta^TX^T)(y - X\theta) + \frac{\lambda}{2}\theta^T\theta
\\\\
& = \frac{1}{2}(y^Ty - \theta^TX^Ty - y^TX\theta + \theta^TX^TX\theta) + \frac{\lambda}{2}\theta^T\theta
\\\\\\
\frac{\partial E}{\partial \theta} & =
\frac{1}{2}(-X^Ty - X^Ty + 2X^TX\theta) + \lambda\theta
\\\\
& = X^T(X\theta - y) + \lambda\theta
\end{split}
\]
令微分为0,得到解析解:
\[\begin{split}
\frac{\partial E}{\partial \theta}
& = X^T(X\theta - y) + \lambda\theta
\\\\
& = -X^Ty + X^TX\theta + \lambda\theta
\\\\
& = 0
\\\\\\
\theta &= (X^TX + \lambda I)^{-1}X^Ty
\end{split}
\]
其中 \(I\) 为 单位矩阵 (主对角线元素全部为1,其余元素全部为0)
1.2 梯度下降法求解岭回归
岭回归 中的 参数更新表达式:
\[\theta_j := \theta_j - \eta \sum_{i=1}^n(f_{\theta}(x^{(i)} - y^{(i)}))x^{(i)}_j - \eta\lambda \theta_j
\]
向量化表示参数更新表达式:
\[\theta := \theta - \eta X^T(X\theta - y) - \eta\lambda\theta
\]
1.3 岭回归 代码
# 岭回归解析解
def ridge_reg(x, y, lam=0.2):
deno = X.T * X + np.eye(X.shape[1]) * lam
return deno.I * (X.T * Y)
2. LASSO回归
2.1 LASSO回归 L1正则化
与岭回归相似,LASSO回归 同样是通过添加正则项来改进朴素最小二乘法,其采用的时 L1正则化,也就是添加了 惩罚项 \(\frac{\lambda}{2}||\theta||_1\),即 \(\frac{\lambda}{2}\sum_{j = 1}^d|\theta_j|\) .
此时,损失函数 如下:
\[E = \frac{1}{2}\sum_{i = 1}^{n}(y^{(i)} - f_{\theta}(x^{(i)}))^2 + \frac{\lambda}{2}\sum_{j = 1}^d|\theta_j|
\]
求偏微分:
\[\frac{\partial E}{\partial \theta_j} = \sum^n_{i=1}(f_{\theta}(x^{(i)}) - y^{(i)})x^{(i)}_j +
\begin{cases}
-\lambda & \theta_j < 0
\\
[-\lambda, \lambda] & \theta_j = 0
\\
\lambda & \theta_j > 0
\end{cases}
\]
令偏微分为0:
\[\theta_k =
\begin{cases}
\frac{p_k + \frac{\lambda}{2}}{z_k} & p_k < \frac{\lambda}{2}
\\
0 & -\frac{\lambda}{2} \le p_k \le \frac{\lambda}{2}
\\
\frac{p_k - \frac{\lambda}{2}}{z_k} & p_k > \frac{\lambda}{2}
\end{cases}
\]
参考文章
机器学习算法实践-岭回归和LASSO
岭回归、LASSO回归(包括公式推导)
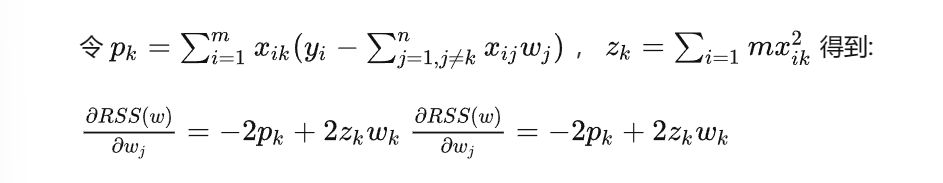


 浙公网安备 33010602011771号
浙公网安备 33010602011771号