[机器学习复习笔记] RNN 循环神经网络
RNN 循环神经网络
1. RNN
1.1 RNN 示意图及时序展开
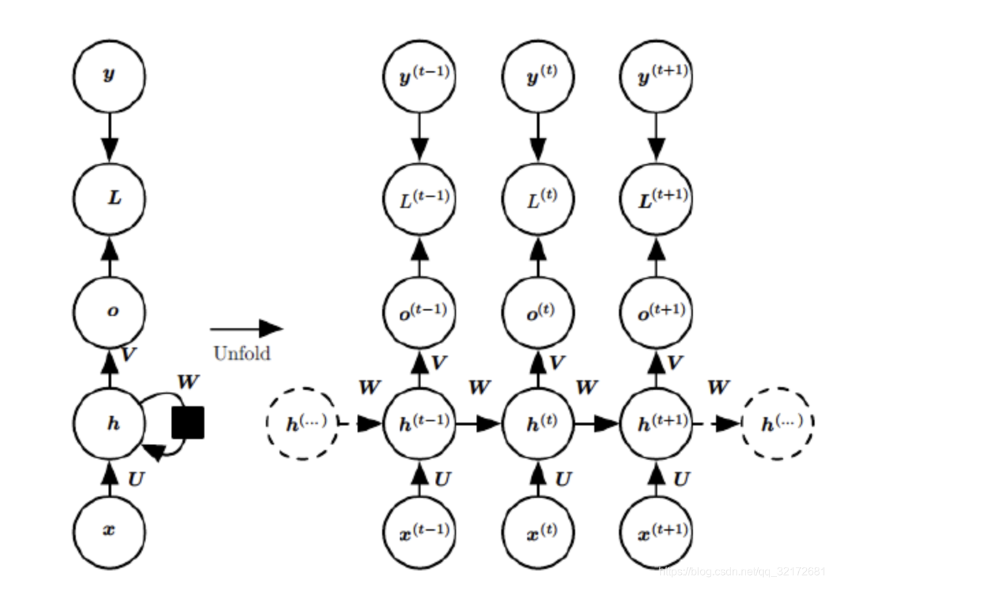
-
\(x^{(t)}\) 表示输入层的输入
-
\(U\) 为输入层到隐藏层的权值参数
-
\(h^{(t)}\) 表示隐藏层的输出,激活函数一般为 \(\text{tanh}\) 或 \(\text{ReLU}\)
-
\(W\) 为上一时刻的隐藏层到隐藏层的权值参数
-
\(o^{(t)}\) 为输出层的输出,激活函数一般为 \(\text{Softmax}\)
-
\(V\) 为隐藏层到输出层的权值参数
-
\(L^{(t)}\) 为损失函数
-
\(y^{(t)}\) 为时刻 \(t\) 样本给出的值
1.2 RNN 状态更新公式
\(f\) 一般为 \(\text{tanh}\) 或 \(\text{ReLU}\) 函数;\(g\) 一般为 \(\text{Softmax}\) 函数。
PS:
-
可以将 \(h^{(t)}\) 看作网络记忆,其捕获了先前所有时间步骤中的信息。每一步的 \(o^{(t)}\) 根据时间 \(t\) 的记忆进行计算,可以看出循环神经网络对历史信息进行了保存。
-
示意图及时序展开图中,每个时间步都有输出,但不是必需的,需要根据实际任务决定。由此可以有如下组合:
-
多输入,单输出
-
单输入,多输出
-
多输入,多输出(输出与输入数量相同)
-
多输入,多输出(输出与输入数量不同)

-
此处感谢 知乎 ARGO创新实验室 的图片,出处:循环神经网络(RNN)知识入门
1.3 RNN 代码
import torch
import numpy as np
from torch import nn
# RNN模型
class Rnn(nn.Module):
def __init__(self, input_size):
super(Rnn, self).__init__()
# 定义RNN网络
self.rnn = nn.RNN(
input_size=input_size,
hidden_size=32,
num_layers=1, # num_layers是隐藏层数量,RNN为1层
batch_first=True # 输入形状为[批量大小, 数据序列长度, 特征维度]
)
# 定义全连接层
self.out = nn.Linear(32, 1)
# 定义前向传播函数
def forward(self, x, h_0):
r_out, h_n = self.rnn(x, h_0) # 输出层 隐藏层
outs = []
# r_out.size=[1,10,32]即将一个长度为10的序列的每个元素都映射到隐藏层上
for t in range(r_out.size(1)):
# 依次抽取序列中每个单词,将之通过全连接层并输出.r_out[:, 0, :].size()=[1,32] -> [1,1]
outs.append(self.out(r_out[:, t, :]))
# stack函数在dim=1上叠加:10*[1,1] -> [1,10,1] 同时h_n已经被更新
return torch.stack(outs, dim=1), h_n
TIME_STEP = 10
INPUT_SIZE = 1
LR = 0.02
model = Rnn(INPUT_SIZE)
loss_func = nn.MSELoss() # 均方差损失函数
optimizer = torch.optim.Adam(model.parameters(), lr=LR) # 优化器
for step in range(100):
x, y = ...
# 将x通过网络,长度为10的序列通过网络得到最终隐藏层状态h_state和长度为10的输出prediction:[1,10,1]
prediction, h_state = model(x, h_state)
h_state = h_state.data
# 这一步只取了h_state.data.因为h_state包含.data和.grad 舍弃了梯度
# 反向传播
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
# 更新优化器参数
optimizer.step()
2. LSTM
2.1 LSTM 介绍
长短期记忆(Long Short Term Memory,LSTM)网络是一种特殊的RNN模型,其特殊的结构设计使得它可以避免长期依赖问题,记住很早时刻的信息是LSTM的默认行为,而不需要专门为此付出很大代价。
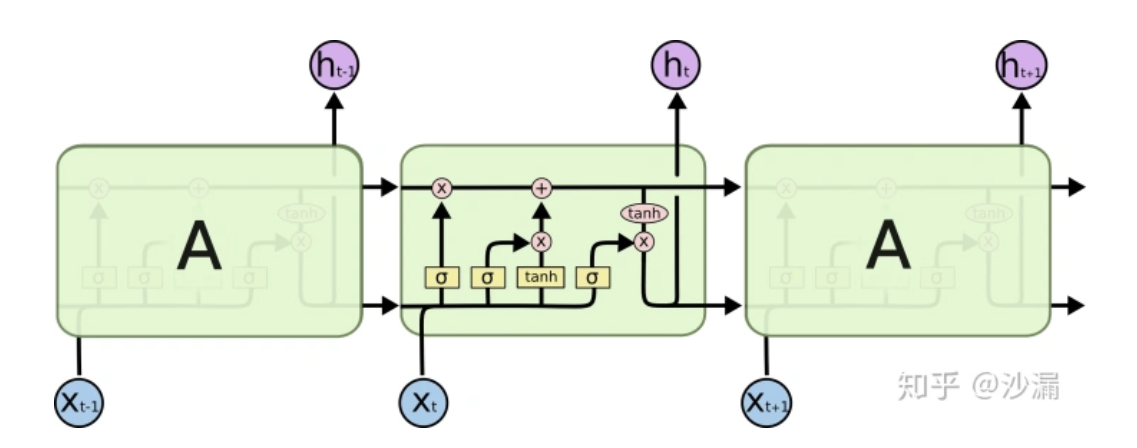
此处感谢 知乎 沙漏 的图片,出处:[干货]深入浅出LSTM及其Python代码实现
-
黄色方块:表示一个神经网络层(Neural Network Layer)
-
粉色圆圈:表示按位操作或逐点操作(pointwise operation),例如向量加和、向量乘积等
-
\(x^{(t)}\) 为输入层输入
-
\(h^{(t)}\) 为隐藏层输出
\(\text{LSTM}\) 主要改变了输入层到隐藏层的传递方式,解决了传统 \(\text{RNN}\) 稳定性不足和梯度消失的问题。
2.2 LSTM 状态更新公式
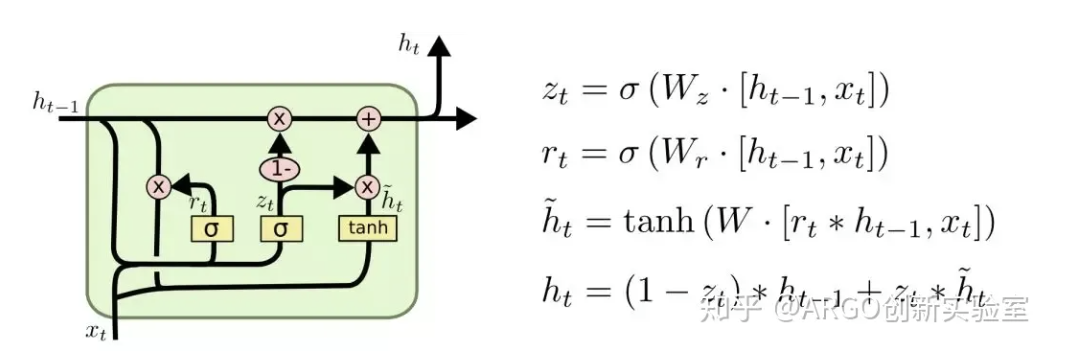
此处感谢 知乎 ARGO创新实验室 的图片,出处:循环神经网络(RNN)知识入门
2.3 LSTM 代码
import numpy as np
import torch
from torch import nn
# Define LSTM Neural Networks
class LstmRNN(nn.Module):
def __init__(self, input_size, hidden_size=1, output_size=1, num_layers=1):
super().__init__()
self.lstm = nn.LSTM(input_size, hidden_size, num_layers) # utilize the LSTM model in torch.nn
self.forwardCalculation = nn.Linear(hidden_size, output_size)
def forward(self, _x):
x, _ = self.lstm(_x) # _x is input, size (seq_len, batch, input_size)
s, b, h = x.shape # x is output, size (seq_len, batch, hidden_size)
x = x.view(s*b, h)
x = self.forwardCalculation(x)
x = x.view(s, b, -1)
return x
if __name__ == '__main__':
...
...
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(lstm_model.parameters(), lr=1e-2)
max_epochs = 100
for epoch in range(max_epochs):
output = lstm_model(train_x_tensor)
loss = loss_function(output, train_y_tensor)
loss.backward()
optimizer.zero_grad()
optimizer.step()
参考文章
一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MarisaMagic/p/17810152.html,未经允许严禁转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号