[数据结构]单向链表及其基本操作(C语言)
单向链表
什么是单向链表
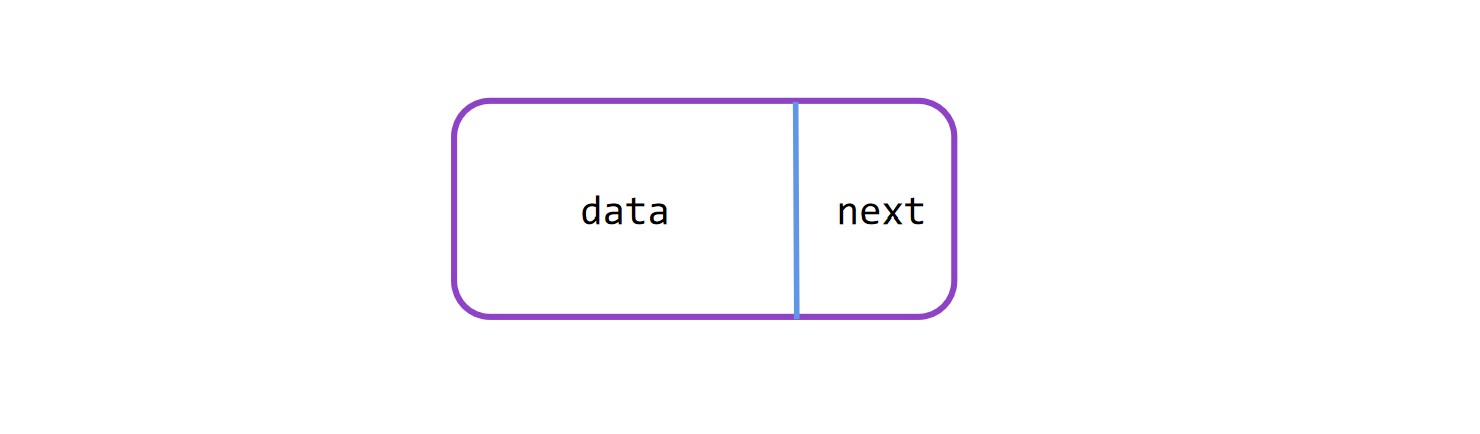
链表是一种物理储存单元上非连续、非顺序的储存结构。它由一系列结点(链表中每一个元素称为结点)组成,结点可动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。
其实可以形象的认为,单向链表就好像一列火车。🤔
链表的节点就好像火车的每一节车厢,而链表节点的数据域就对应车厢中存放的货物,链表节点的指针域充当连接各节车厢的锁链。🥺
为什么需要单向链表
我们知道如何用数组去存储数据。但是在实际应用的过程中,我们有时会出现一些不可避免的问题:
问题1
假如定义了并初始化一个数组 a[5] = {1,2,3,4,5}, 此时要在加入新的元素,只能开辟一个更大的数组。
问题2
假如定义一个数组 a[100000], 但是只存储了几个元素,会导致浪费空间。
而单向链表这样链式的动态存储的数据结构,恰恰解决了使用数组时若数组已满无法插入新的数据的问题,以及使用数组时可能浪费大量存储空间的问题。🧐
单向链表的创建
单个链表节点的构成
首先看一下单向链表节点的结构体,我们把单个节点看作是一节车厢,数据域就好像车厢存储的货物,指针域就好像锁链。
typedef int Elemtype; //数据类型
typedef struct Node {
Elemtype data; //结构体数据域
struct Node *next; //结构体指针域
} Linklist;
链表的初始化创建
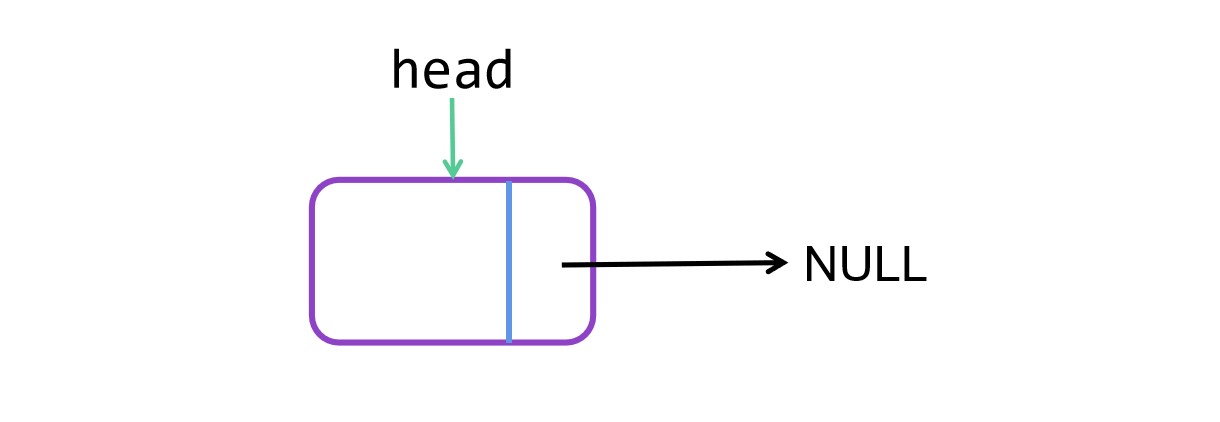
链表一般需要一个头节点,这个头结点一般是不带数据的。可以看作是驱动火车前进的火车头。
//链表的初始化
Linklist* Initial_linklist(){
//向系统申请内存
Linklist *head = (Linklist *)malloc(sizeof(Linklist));
head->next = NULL;
return head;
}
链表初始数据插入
单向链表的初始数据可以是任意个,此处采用的是尾插法,后面会具体解释这个方法。
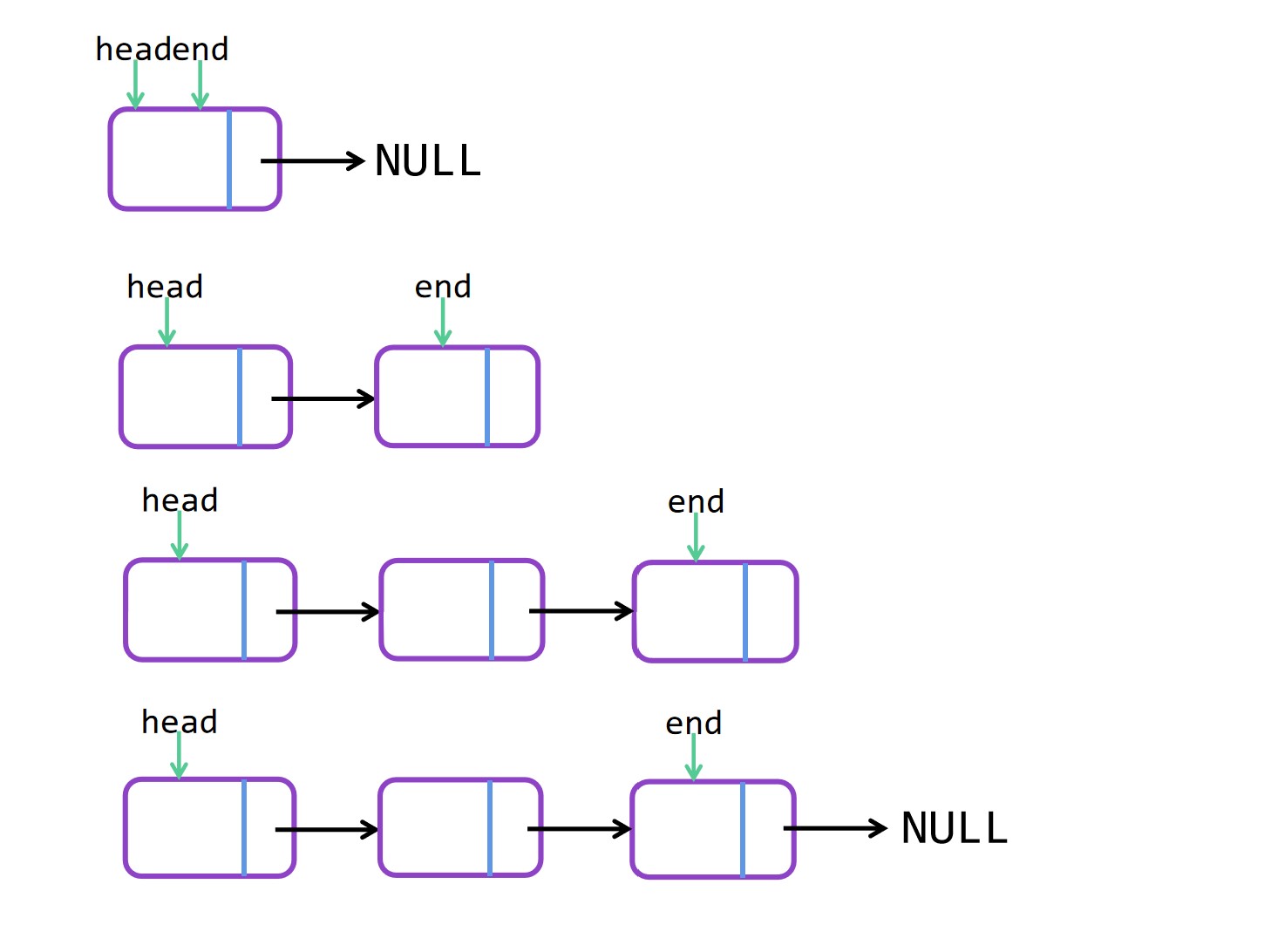
//创建初始链表 采用尾插法
void Create_linklist(Linklist *head, int n) {
Linklist *node, *end; //普通节点 尾节点
end = head; //当链表为空时 头尾指向同一个节点
printf("创建链表输入 %d 个元素:", n);
for (int i = 0; i < n; i++) { //n为插入普通节点的个数
node = (Linklist *)malloc(sizeof(Linklist));
scanf("%d", &node->data);
end->next = node; //当前end的next指向了新节点node
end = node; //end往后移,此时新的节点变成尾节点
}
end->next = NULL; //end最后置NULL
}
单向链表的基本操作
头插法 插入单个数据
头插法图解
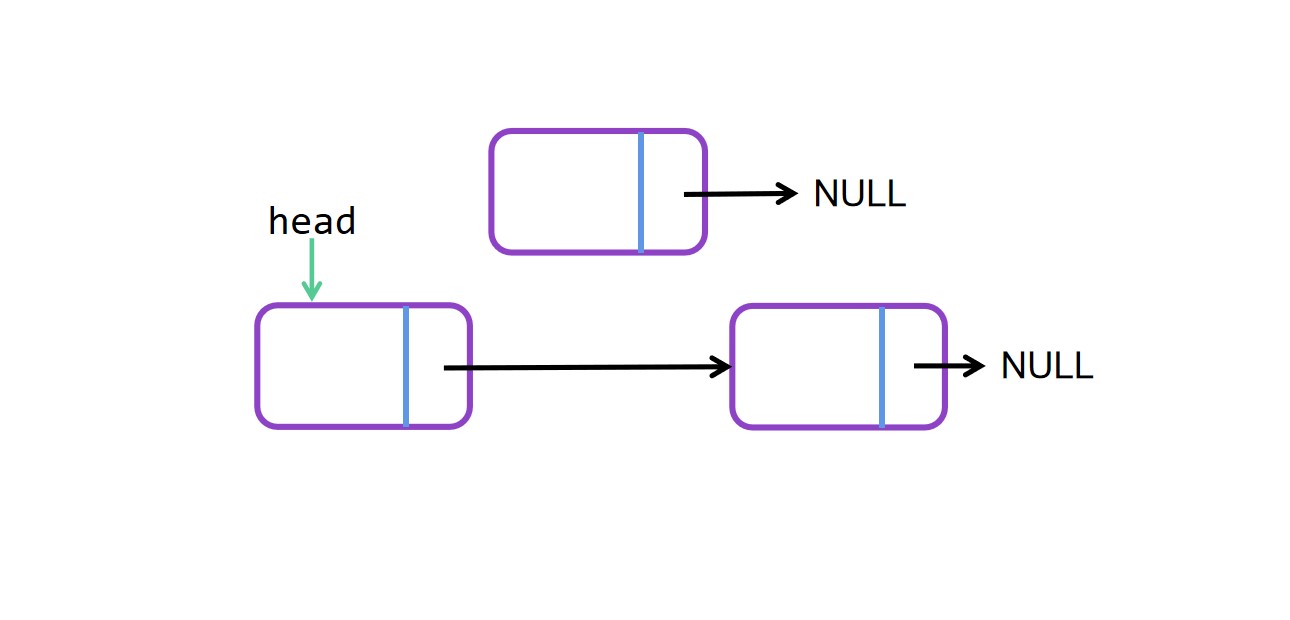
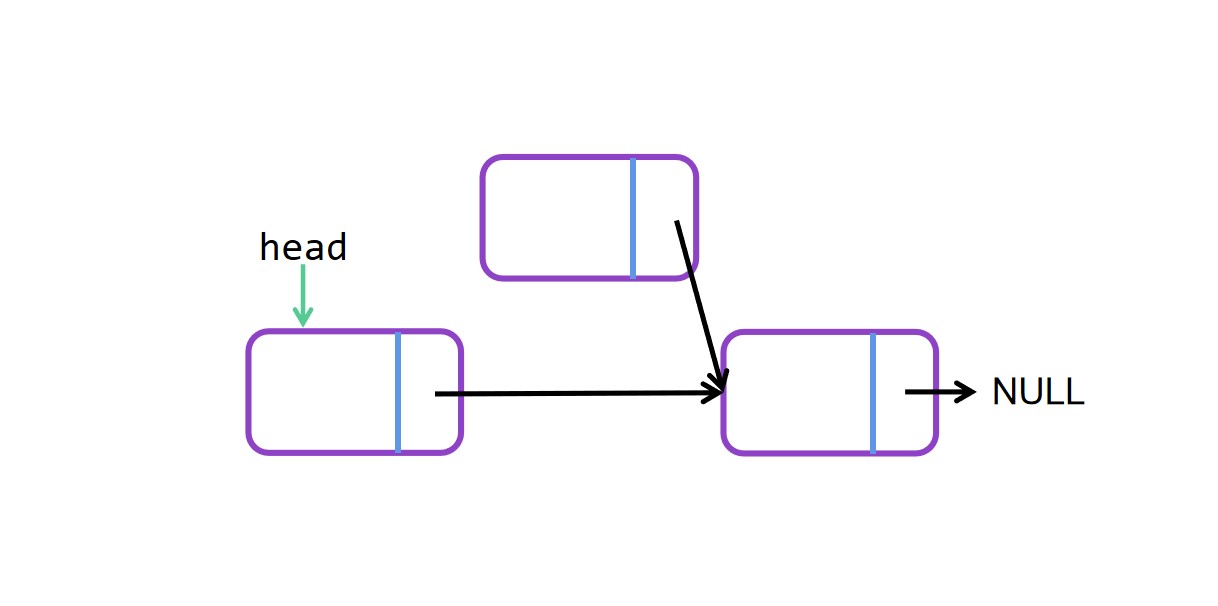
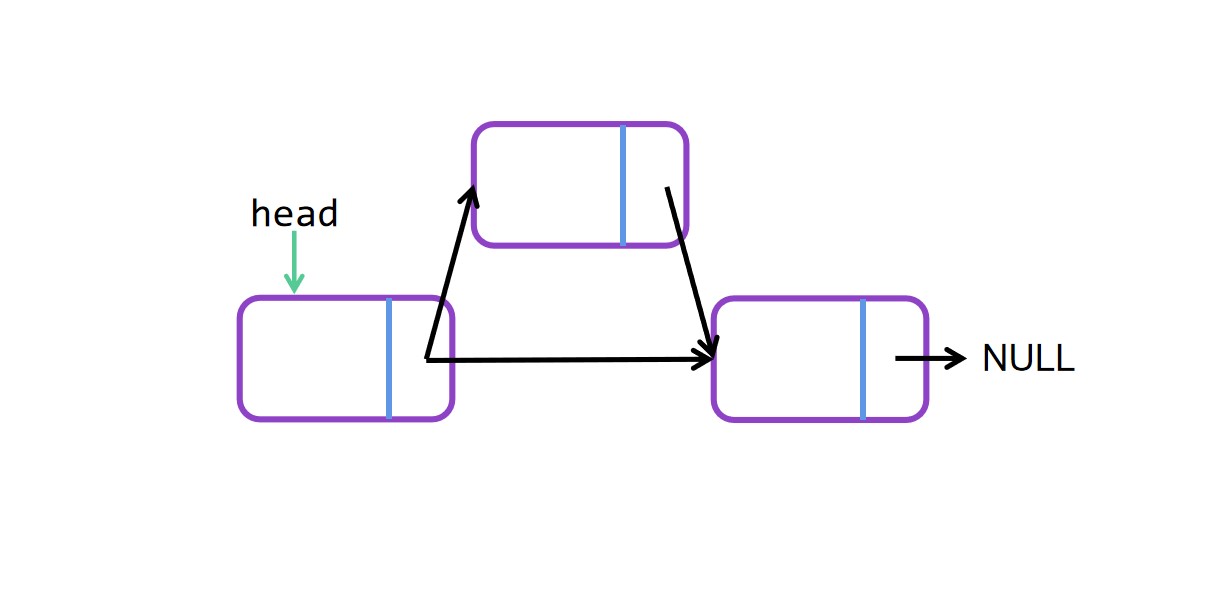
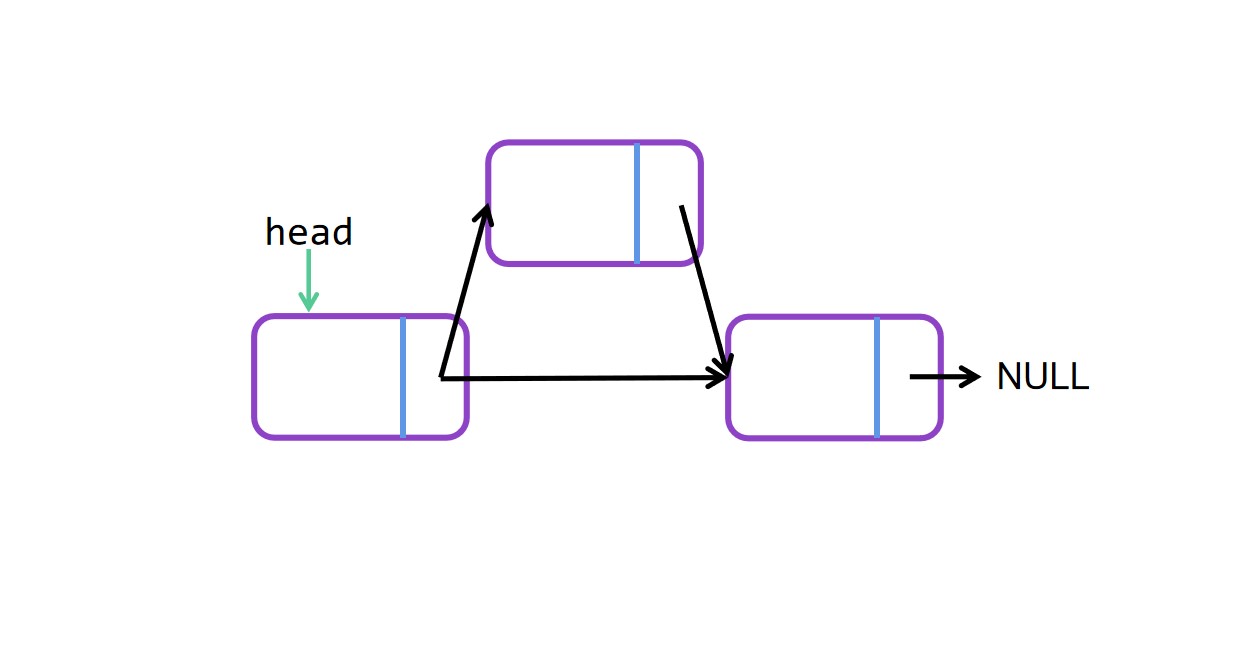
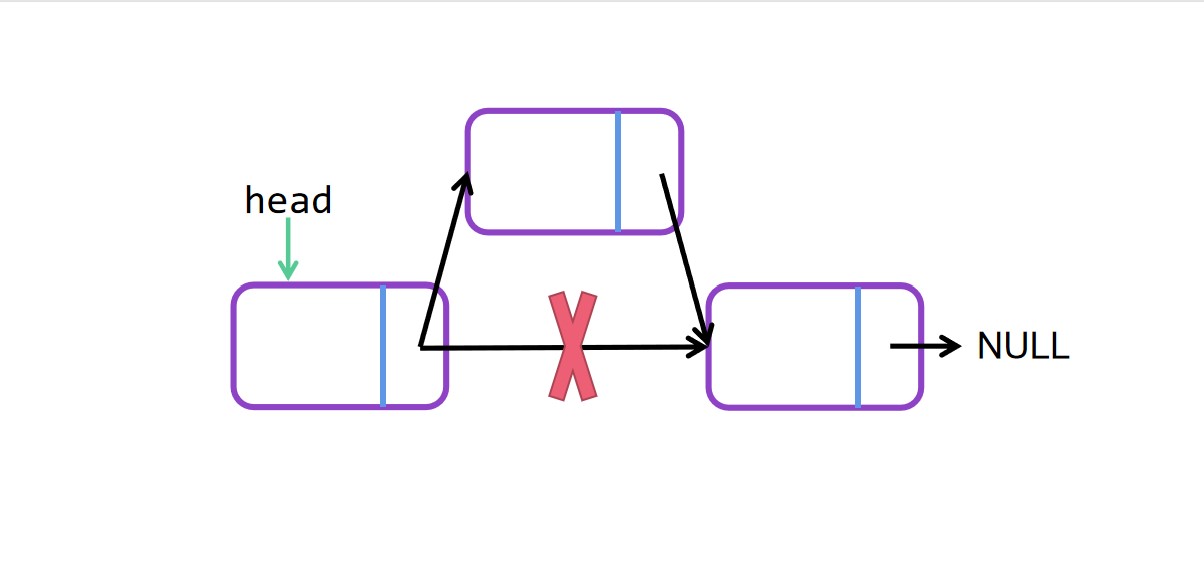
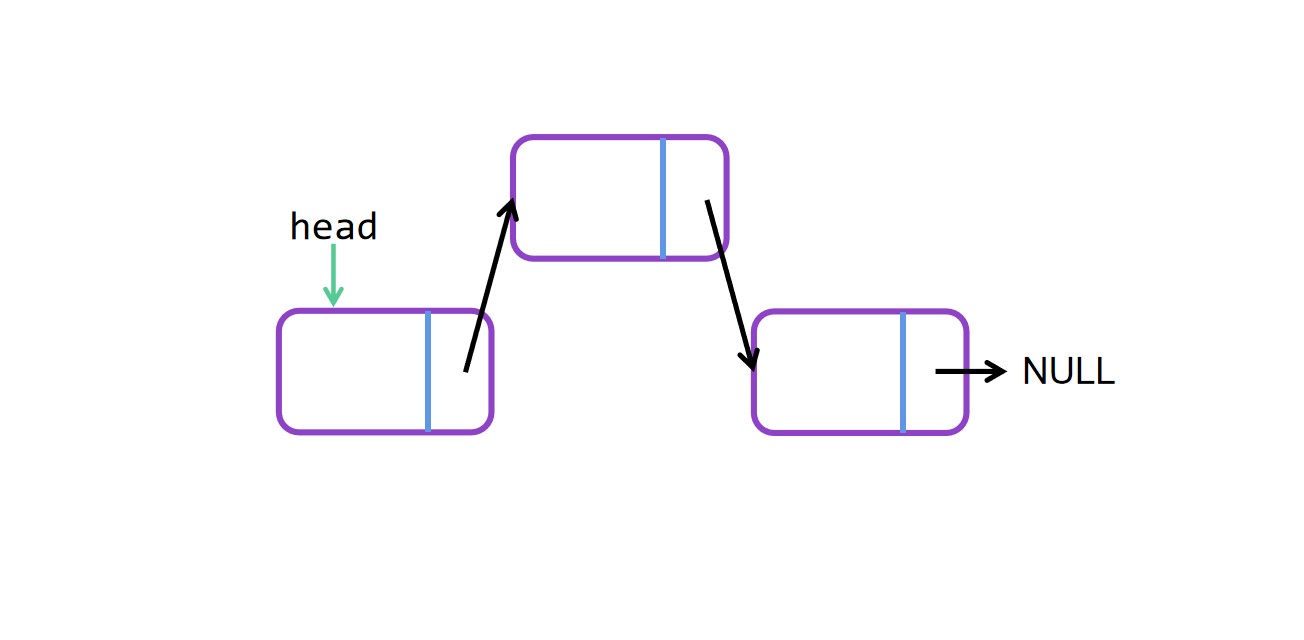
头插法代码
//头插法 插入单个数据
void Insert_Front(Linklist *head, int data) {
Linklist *node = (Linklist *)malloc(sizeof(Linklist));
node->next = NULL;
node->data = data;
node->next = head->next; //新节点node的next指向当前head的next
head->next = node; //head的next重新指向新节点node
}
尾插法 插入单个数据
尾插法图解
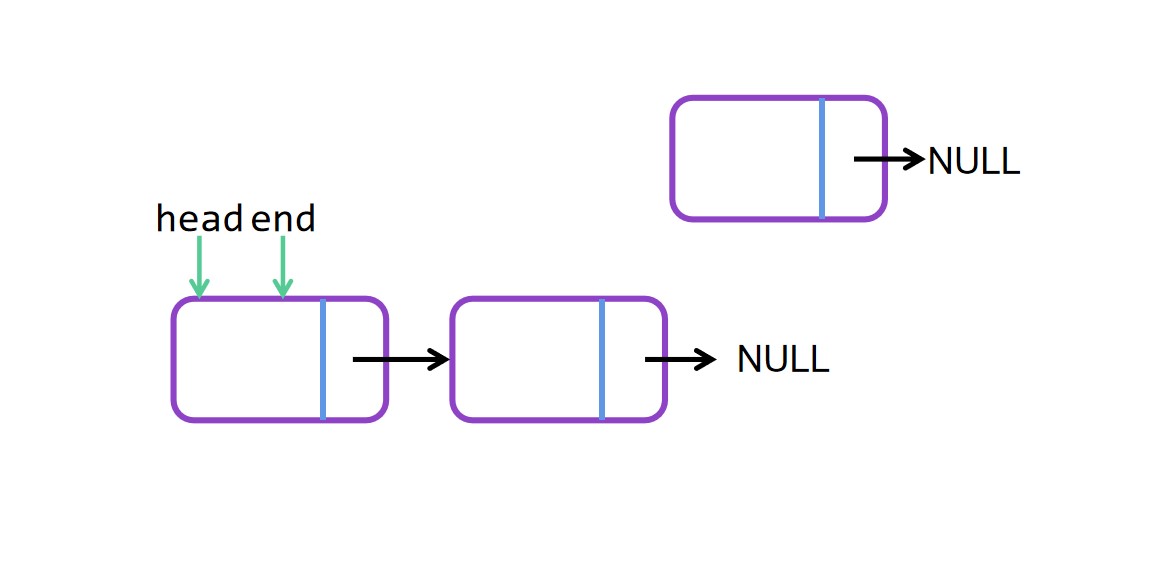
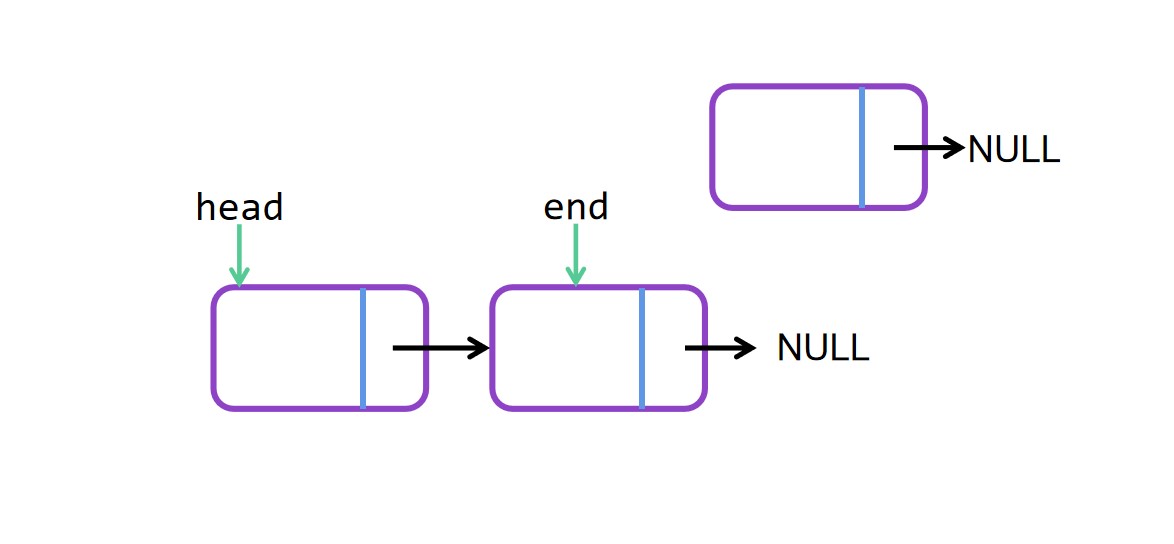
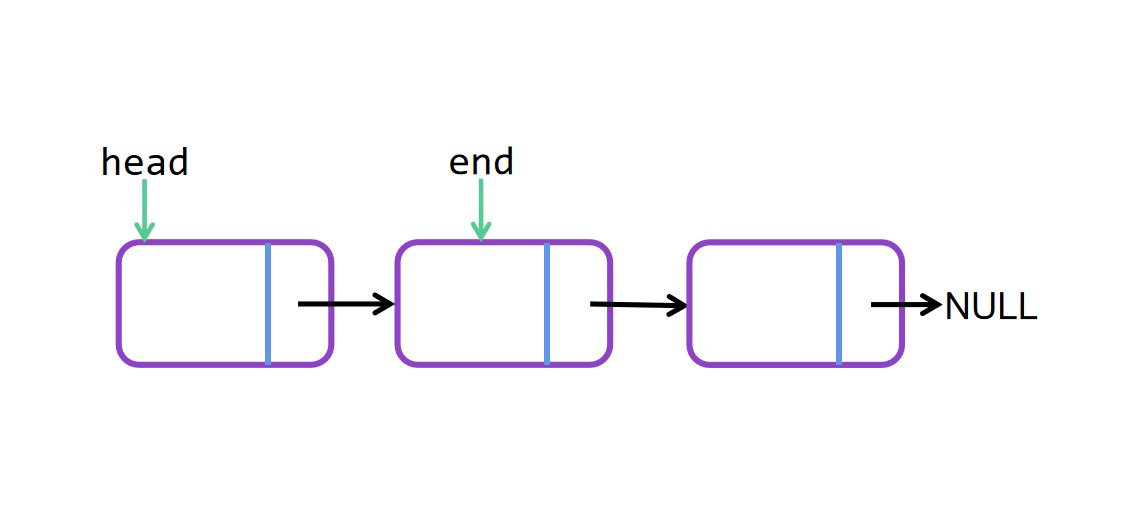
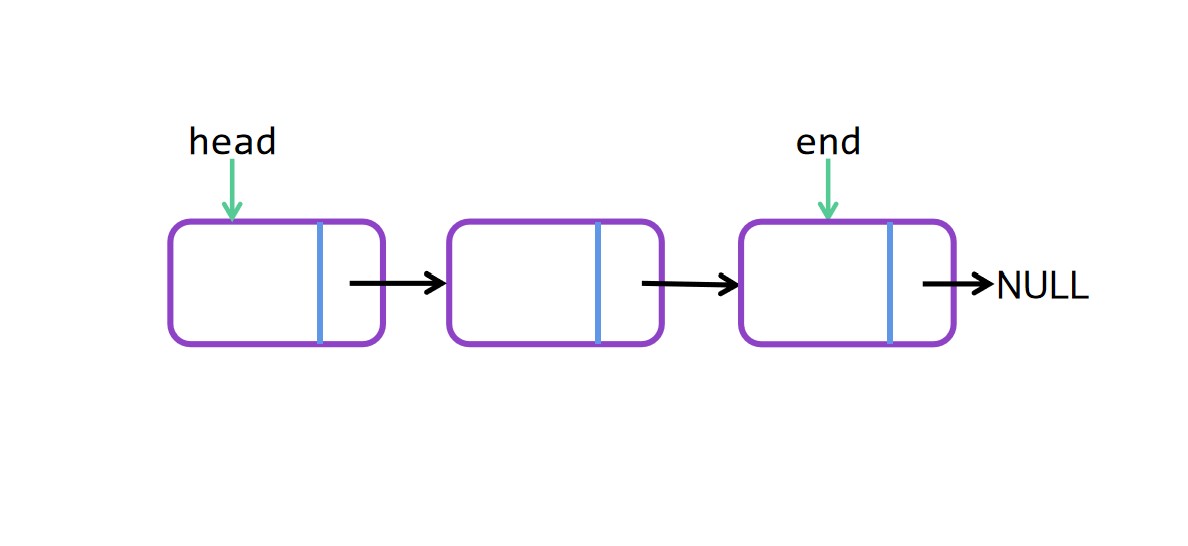
尾插法代码
//尾插法 插入单个数据
void Insert_Back(Linklist *head, int data) {
Linklist *node = (Linklist *)malloc(sizeof(Linklist));
node->next = NULL;
node->data = data;
Linklist *end = head; //起初end指向头节点
while (end->next != NULL)
end = end->next; //end指针往后移,直到最后一个节点
end->next = node; //当前end的next指向了新节点node
}
指定位置插入节点
分析及解释
指定位置插入单个数据,这里一般设定为在第 k 个带数据的普通节点(除去头节点)位置插入一个新的节点。其实指定位置插入新节点的原理和头插法是类似的,只不过是将第 k 个带数据节点的前一个节点看成头结点一样。因此我们需要找到第 k-1 个带数据节点,假如遍历指针 t 从头节点开始,那么算上头节点,需要经历 k-1 次循环找到第 k-1 个带数据节点。值得注意的是,如果k = 1的话,也就是在第一个带数据节点的位置插入新节点,不存在第0个带数据节点,此时其实这个第 k-1 个节点就变成了头节点。那么此时明显和头插法是完全一样的。
图解的话可以参考头插法的图解,是差不多的。🥺
指定位置插入单个数据 代码
//指定位置插入单个节点
void Insert_position(Linklist *head, int k) {
//k表示在第k个普通节点的位置插入新节点
Linklist *t = head, *in; //t为遍历指针
//in是要插入的新节点
for (int i = 0; i < k - 1; i++)
t = t->next;
if (t != NULL) {
in = (Linklist *)malloc(sizeof(Linklist));
in->next = NULL;
printf("在第 %d 个节点处插入新节点的数据: ", k);
scanf("%d", &in->data);
in->next = t->next; //插入节点in的next指向当前第k-1个普通节点的next指向的节点
t->next = in; //第k-1个普通节点的next重新指向插入的节点in
//原理和头插法类似 就好像把第k-1个普通节点t看做是头节点
} else {
puts("节点不存在");
}
}
遍历输出链表数据
分析及解释
我们需要用指针去访问链表中的数据。定义了一个指针t,来对链表的每一个存有数据的节点进行访问并读取数据,直到当前节点为NULL,停止遍历。
通俗地来说,就好比一个卸货员工,他挨个从头到尾取下每一节火车车厢的货物,直到最后到达尾部车厢的时候,他便不再取下货物。🤗
打印链表代码
//打印链表
void Show_linklist(Linklist *head) {
Linklist *t = head->next; //t为遍历指针 访问每个节点数据
if (t == NULL)
puts("链表为空");
while (t != NULL) {
printf("%d ", t->data);
t = t->next;
}
printf("\n\n");
}
指定位置删除节点
分析及解释
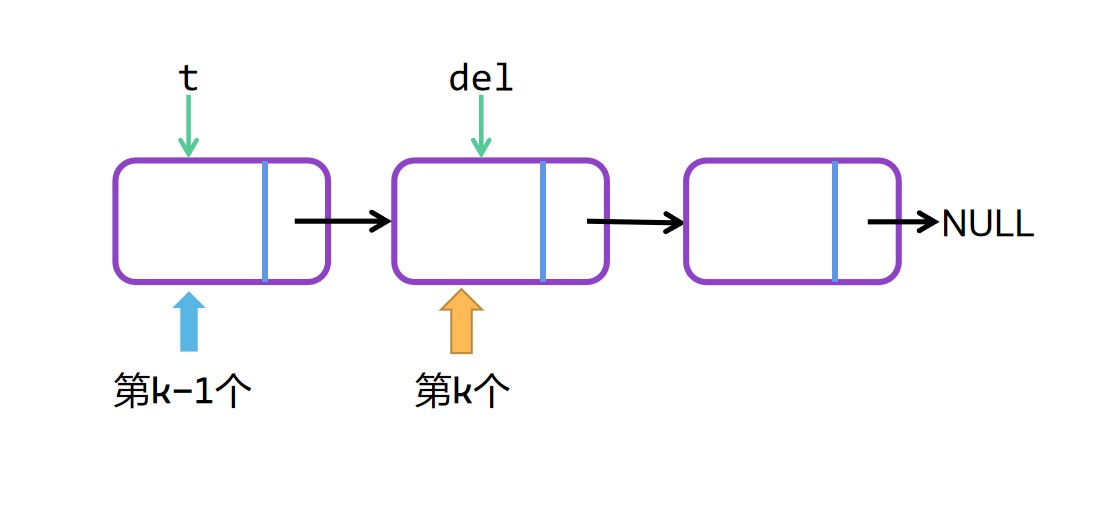
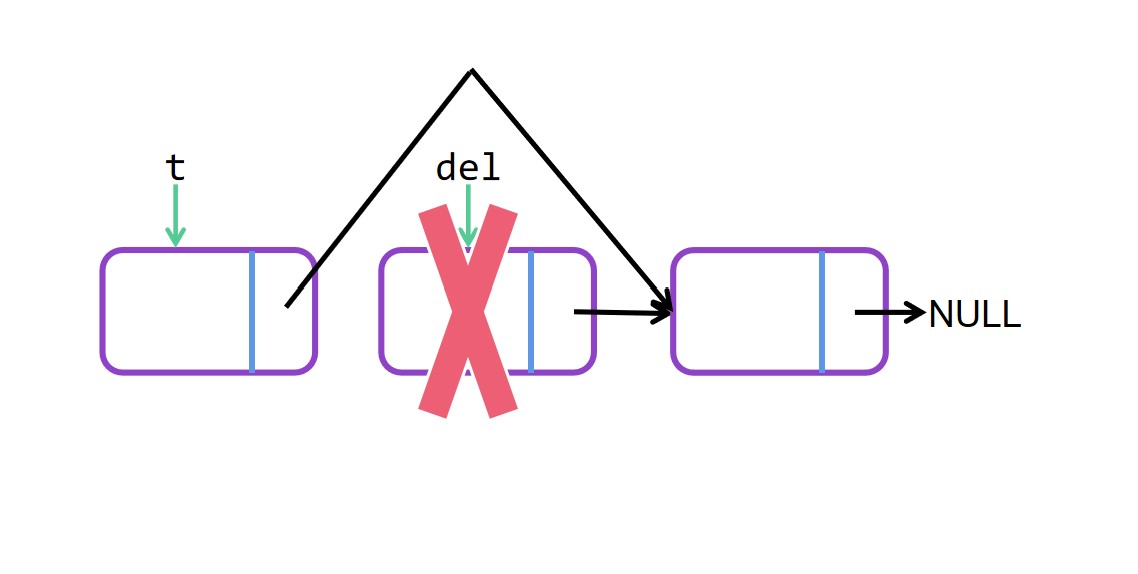
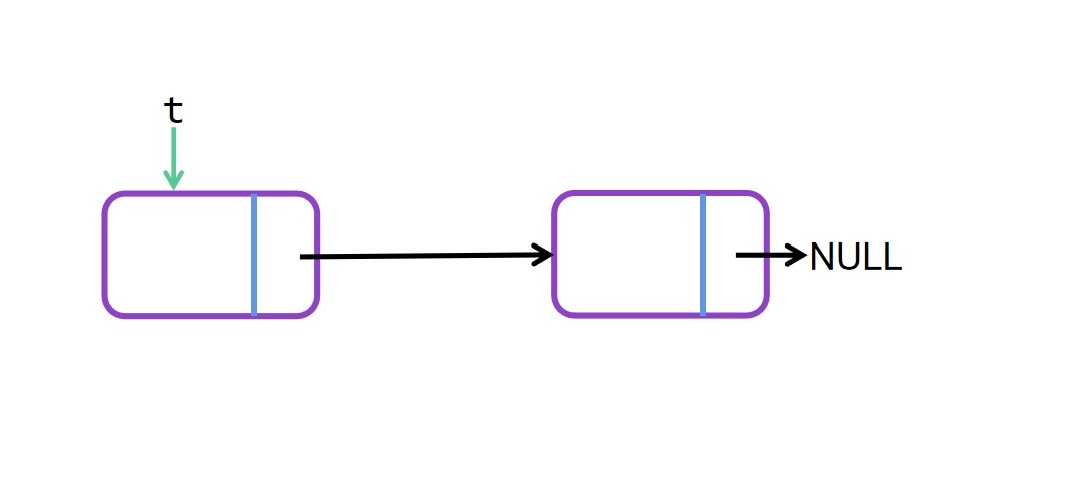
删除单个节点很容易,只需要找到要删除的节点的前一个节点,然后直接跨过中间这个删除的节点指向删除节点的下一个节点就可以了。
指定位置删除节点 图解
指定位置删除节点 代码
void Delete_position(Linklist *head, int k) { //k表示要删除第k个节点
Linklist *t = head, *del = NULL; //t为遍历指针
int i = 0;
while (i < k - 1 && t != NULL) {
t = t->next; //t指向删除的第k个的前一个节点
i++;
}
if (t != NULL) {
del = t->next;
t->next = del->next;
free(del);
} else {
puts("节点不存在");
}
}
其他基本操作
其他基本操作代码
//查找元素返回节点位置
void Find_Element(Linklist *head, int x) {
Linklist *t = head->next;
while (t != NULL) {
int sub = 1;
if (t->data == x)
printf("元素 %d 的位置为: %d \n", x, sub);
t = t->next;
sub++;
}
if (t == NULL)
puts("元素不存在");
}
//读取指定节点位置元素
void Read_position(Linklist *head, int k) {
Linklist *t = head->next;
for (int i = 0; i < k; i++)
t = t->next;
printf("第 %d 个节点位置的数据为: %d \n", k, t->data);
}
//计算链表的长度
void List_length(Linklist *head){
Linklist *t = head->next;
int len = 0;
while(t){
len++;
t = t->next;
}
printf("链表的长度为: %d \n", len);
}
//清空链表
void Clear_linklist(Linklist *head) {
Linklist *t;
while (head->next != NULL) {
t = head->next;
head->next = t->next;
free(t);
}
}
//判断是否为空
bool IsEmpty(Linklist *head){
return head->next == NULL;
}
链表的奇偶项拆分
//拆分链表为两个链表 奇偶项拆分
void Depart_linklist(Linklist *head, Linklist *la, Linklist *lb){
Linklist *t = head->next;
Linklist *ra = la, *rb = lb; //尾指针 尾插法
while(t){
ra->next = t; //表a
ra = t;
t = t->next;
rb->next = t; //表b
rb = t;
t = t->next;
}
ra->next = rb->next = NULL;
}
完整程序
完整程序源代码
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef int Elemtype; //数据类型
typedef struct Node {
Elemtype data; //结构体数据域
struct Node *next; //结构体指针域
} Linklist;
//链表的初始化
Linklist* Initial_linklist(){
//向系统申请内存
Linklist *head = (Linklist *)malloc(sizeof(Linklist));
head->next = NULL;
return head;
}
//创建初始链表 采用尾插法
void Create_linklist(Linklist *head, int n) { //头节点(不带数据)
Linklist *node, *end; //普通节点 尾节点
end = head; //当链表为空时 头尾指向同一个节点
printf("创建链表输入 %d 个元素:", n);
for (int i = 0; i < n; i++) { //n为插入普通节点的个数
node = (Linklist *)malloc(sizeof(Linklist));
scanf("%d", &node->data);
end->next = node; //当前end的next指向了新节点node
end = node; //end往后移,此时新的节点变成尾节点
}
end->next = NULL; //end最后置NULL
}
//打印链表
void Show_linklist(Linklist *head) {
Linklist *t = head->next; //t为遍历指针 访问每个节点数据
if (t == NULL)
puts("链表为空");
while (t != NULL) {
printf("%d ", t->data);
t = t->next;
}
printf("\n\n");
}
//头插法 插入单个数据
void Insert_Front(Linklist *head, int data) {
Linklist *node = (Linklist *)malloc(sizeof(Linklist));
node->next = NULL;
node->data = data;
node->next = head->next; //新节点node的next指向当前head的next
head->next = node; //head的next重新指向新节点node
}
//尾插法 插入单个数据
void Insert_Back(Linklist *head, int data) {
Linklist *node = (Linklist *)malloc(sizeof(Linklist));
node->next = NULL;
node->data = data;
Linklist *end = head; //起初end指向头节点
while (end->next != NULL)
end = end->next; //end指针往后移,直到最后一个节点
end->next = node; //当前end的next指向了新节点node
}
//指定位置插入单个数据
void Insert_position(Linklist *head, int k) { //k表示在第k个普通节点的位置插入新节点
Linklist *t = head, *in; //t为遍历指针
//in是要插入的新节点
for (int i = 0; i < k - 1; i++)
t = t->next;
if (t != NULL) {
in = (Linklist *)malloc(sizeof(Linklist));
in->next = NULL;
printf("在第 %d 个节点处插入新节点的数据: ", k);
scanf("%d", &in->data);
in->next = t->next; //插入节点in的next指向当前第k-1个普通节点的next指向的节点
t->next = in; //第k-1个普通节点的next重新指向插入的节点in
//原理和头插法类似 就好像把第k-1个普通节点t看做是头节点
} else {
puts("节点不存在");
}
}
//指定位置改变节点的数据
void Change_position(Linklist *head, int n) { //n表示要改变的是第n个普通节点
Linklist *t = head; //t为遍历指针
for (int i = 0; i < n; i++)
t = t->next; //t指向要改变的节点
if (t != NULL) {
printf("修改第 %d 个节点的数据: ", n);
scanf("%d", &t->data);
} else {
puts("节点不存在");
}
}
//指定位置删除节点
void Delete_position(Linklist *head, int k) { //k表示要删除第k个节点
Linklist *t = head, *del = NULL; //t为遍历指针
int i = 0;
while (i < k - 1 && t != NULL) {
t = t->next; //t指向删除的第k个的前一个节点
i++;
}
if (t != NULL) {
del = t->next;
t->next = del->next;
free(del);
} else {
puts("节点不存在");
}
}
//查找元素返回节点位置
void Find_Element(Linklist *head, int x) {
Linklist *t = head->next;
while (t != NULL) {
int sub = 1;
if (t->data == x)
printf("元素 %d 的位置为: %d \n", x, sub);
t = t->next;
sub++;
}
if (t == NULL)
puts("元素不存在");
}
//读取指定节点位置元素
void Read_position(Linklist *head, int k) {
Linklist *t = head->next;
for (int i = 0; i < k; i++)
t = t->next;
printf("第 %d 个节点位置的数据为: %d \n", k, t->data);
}
//计算链表的长度
void List_length(Linklist *head){
Linklist *t = head->next;
int len = 0;
while(t){
len++;
t = t->next;
}
printf("链表的长度为: %d \n", len);
}
//清空链表
void Clear_linklist(Linklist *head) {
Linklist *t;
while (head->next != NULL) {
t = head->next;
head->next = t->next;
free(t);
}
}
//判断是否为空
bool IsEmpty(Linklist *head){
return head->next == NULL;
}
int main() {
//头指针初始化
Linklist *mylist;
mylist = Initial_linklist();
Create_linklist(mylist, 10);
printf("初始状态链表:\n");
Show_linklist(mylist);
Insert_Front(mylist, 30);
Insert_Back(mylist, 30);
printf("链表进行首尾插入数字30后:\n");
Show_linklist(mylist);
Insert_position(mylist, 5);
printf("链表进行在第5个节点后插入新节点后:\n");
Show_linklist(mylist);
Change_position(mylist, 4);
printf("链表进行改变第4个数据后:\n");
Show_linklist(mylist);
Delete_position(mylist, 1);
printf("链表进行删除第1个数据后:\n");
Show_linklist(mylist);
Clear_linklist(mylist);
printf("链表进行清空后:\n");
if(IsEmpty(mylist))
puts("链表为空");
return 0;
}
程序运行结果图

一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MarisaMagic/p/17000467.html,未经允许严禁转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号