[排序算法] 桶排序 (C++)
桶排序解释
桶排序思想
桶排序 是一种空间换取时间的排序方式,是非基于比较的。
桶排序 顾名思义,就是构建多个映射数据的桶,将数据放入桶内,对每个桶内元素进行单独排序。假设我们有 n 个待排序的元素,我们定义了 k 个桶,之后将这 n 个元素分配到 k 个桶中。我们一般每个桶的数据范围大小是 10。若某个元素为 x,那么它会被放到 编号为 x/10 的桶内。这其实就像是计数排序的升级版本,相较计数排序(若把计数排序统计数组每项看作是一个桶),桶变得少了很多。
(如还有对计数排序不了解的童鞋 可以看看这里哟~ 计数排序)
在单独对桶内元素进行排序时,我们一般使用其他的排序方式,用的比较多的是快速排序sort (因为比较快🥴🥴🥴)。
桶排序动态演示
将元素放入桶内

对桶内元素排序后放回原数组
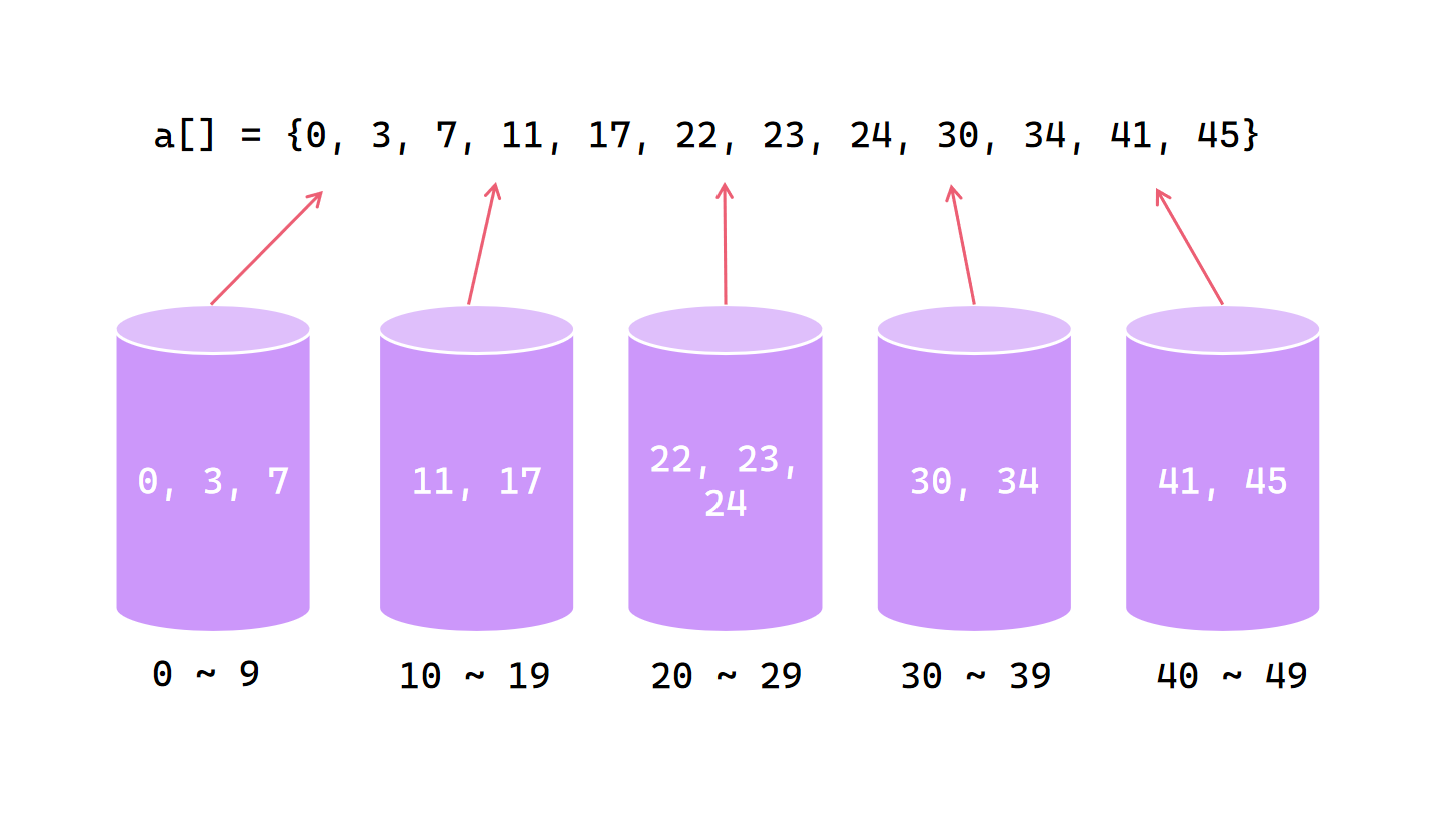
桶排序时间复杂度
最优时间复杂度
假设有 n 个元素,恰好均匀地分配到 k 个桶中。分配过程我们需要消耗 O(n) 的时间,对每个桶单独排序,消耗了 kO((n/k)log(n/k))* 的时间,化简可得 nO(log(n/k))*。我们一般设 c = log(n/k), 由此的时间复杂度为 O(n + c) 。在极端情况下,我们的元素个数和桶的个数十分接近时,即 n = k 时,我们都不需要进行桶内排序,此时的时间复杂度为 O(n)。
最坏时间复杂度
如果 n 个元素分配到 k 个桶中非常地不均匀,我们的每一个桶之间,有的桶中元素非常多,有的则非常少,那么对于那个元素非常多的桶,我们需要很多时间去进行桶内排序。极端情况下,假设有两个桶,其中一个有10000个元素,另一个只有一个元素,那么我们的时间消耗几乎和使用的桶内排序算法的时间复杂度几乎无异。O(n + log(n/k)) 其中 n远大于k,那么时间复杂度几乎就是 O(nlogn) 了。 🥺🥺🥺
对于上述情况,如果我们想着用超多的桶来解决的话,又会造成很多空桶的出现,那么我们浪费的空间是很多的(浪费可耻呀!😤)。
桶排序核心代码
//桶排序 设置几个桶,放入元素并对桶内排序(采用sort)
void BucketSort(vector<int> &a){
int n = a.size();
vector<vector<int>> bucket(N);
for(int i = 0; i < n; i++)
bucket[a[i] / 10].push_back(a[i]);
//将每个元素放入对应桶中
int k = 0;
for(int i = 0; i < N; i++){
//对每个桶进行排序
sort(bucket[i].begin(), bucket[i].end());
int size = bucket[i].size();
for(int j = 0; j < size; j++)
a[k++] = bucket[i].at(j); //放入原数组
}
vector<vector<int>>().swap(bucket); //释放空间
}
完整程序源代码
#include<iostream>
#include<vector>
#include<algorithm> //sort
#include<ctime>
using namespace std;
const int N = 10; //桶的个数 数据范围设为0 - 100(左闭右开)
//桶排序 设置几个桶,放入元素并对桶内排序(采用sort)
void BucketSort(vector<int> &a){
int n = a.size();
vector<vector<int>> bucket(N);
for(int i = 0; i < n; i++)
bucket[a[i] / 10].push_back(a[i]);
//将每个元素放入对应桶中
int k = 0;
for(int i = 0; i < N; i++){
//对每个桶进行排序
sort(bucket[i].begin(), bucket[i].end());
int size = bucket[i].size();
for(int j = 0; j < size; j++)
a[k++] = bucket[i].at(j); //放入原数组
}
vector<vector<int>>().swap(bucket); //释放空间
}
void show(vector<int> &v){
for(auto &x : v)
cout<<x<<" ";
cout<<endl;
}
main(){
vector<int> a;
srand((int)time(0));
int n = 50;
while(n--)
a.push_back(rand() % 100); //数据范围[0, 99]
show(a);
BucketSort(a);
cout<<endl<<endl;
show(a);
}
程序运行结果图
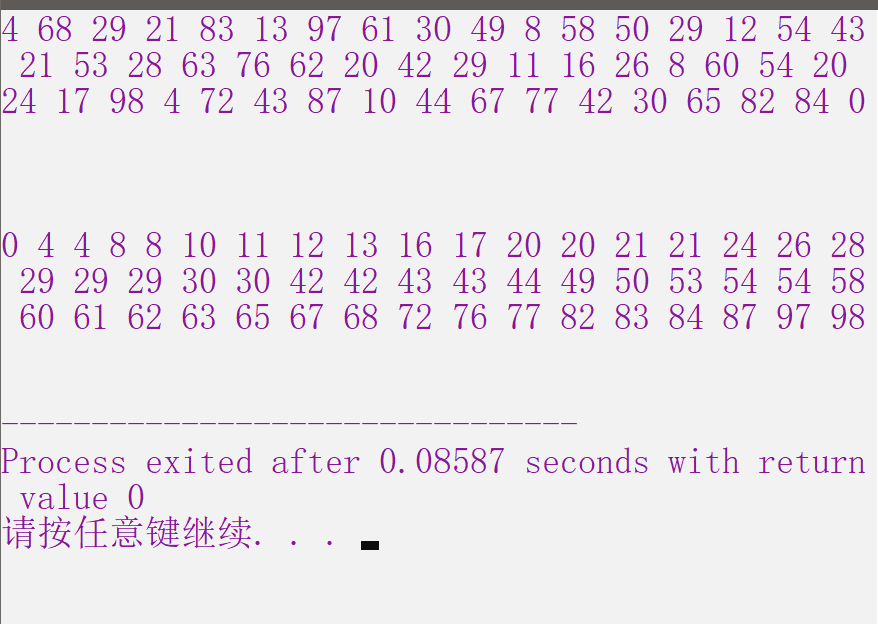
一切都是命运石之门的选择,本文章来源于博客园,作者:MarisaMagic,出处:https://www.cnblogs.com/MarisaMagic/p/16910191.html,未经允许严禁转载


 浙公网安备 33010602011771号
浙公网安备 33010602011771号