2019-第十届蓝桥杯大赛个人赛省赛（软件类）真题 C大学C组

题目一览：

A.求和

【问题描述】
小明对数位中含有2、0、1、9 的数字很感兴趣，在1 到40 中这样的数包括1、2、9、10 至32、39 和40，共28 个，他们的和是574。
请问，在1 到2019 中，所有这样的数的和是多少？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

思路：从1-2019循环，然后将每一个数进行判断有没有2/0/1/9，有的话返回true累积和即可。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 long long Ans;
 5 
 6 bool check(int x) {
 7     while(x) {
 8         int t = x%10;
 9         if(t==2 || t==0 || t==1 || t==9) return true;
10         x /= 10;
11     }
12     return false;
13 }
14 
15 int main() {
16     for(int i=1; i<=2019; ++i) {
17         if(check(i))
18             Ans += i;
19     } 
20     cout << Ans << endl;
21     return 0;
22 }

A.求和

答案：1905111

B.矩形切割

【问题描述】

小明有一些矩形的材料，他要从这些矩形材料中切割一些正方形。

当他面对一块矩形材料时，他总是从中间切一刀，切出一块最大的正方形，剩下一块矩形，然后再切割剩下的矩形材料，直到全部切位正方形为止。

例如，对于一块两边分别为5和3的材料（记为5x3），小明依次切出3x3、2x2、1x1、1x1共4个正方形。

现在小明有一块矩形的材料，两边长分别是2019和324，请问小明最终会切出多少个正方形。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

思路：每次切出以最小边为边长的正方形，然后更新两边长。最后一块若是正方形，则不必继续切。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int main() {
 5     int Ans = 0;
 6 //    int w = 5, h = 3;
 7     int w = 2019, h = 324;
 8     while(w!=0 && h!=0) {
 9         if(w > h) {
10             Ans ++;
11             w -= h;
12         }
13         else if(h > w) {
14             Ans ++;
15             h -= w;
16         }
17         else {
18             Ans ++;
19             break;
20         }
21     } 
22     cout << Ans << endl;
23     return 0;
24 }

B.矩形切割

答案：21

C.年号字串

【问题描述】

小明用字母A 对应数字1，B 对应2，以此类推，用Z 对应26。对于27以上的数字。
小明用两位或更长位的字符串来对应，例如AA 对应27，AB 对应28，AZ 对应52，LQ 对应329。
请问2019 对应的字符串是什么？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

思路：1. 应该很容易看出这就是Excel的编号方式，所以最简单的就是用Excel啦。

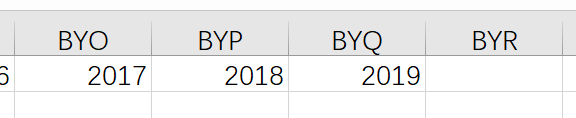
2. 很明显逢27进一位，直接模拟。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int main() {
 5     long long x, y, len=0;
 6     char s[101];
 7 //    scanf("%lld", &x);
 8     x = 2019; 
 9     while(x) {
10         y = x % 26;
11         x /= 26;
12         if(!y) y = 26, x--;
13         s[++len] = 'A' + y - 1;
14     }
15     while(len){
16         printf("%c", s[len--]);
17     }
18     return 0;
19 }

C.年号字串

答案：BYQ

D.质数

【问题描述】

我们知道第一个质数是2、第二个质数是3、第三个质数是5·····请你计算第2019个质数是多少？

思路：直接模拟跑一遍。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 bool check(int x) {
 5     if(x <= 1) return false;
 6     if(x <= 3) return true;
 7     for(int i=2; i*i<=x; ++i) 
 8         if(x%i == 0) return false;
 9     return true;
10 }
11 
12 int main() {
13     int cnt = 0, val = 1;
14     while(true) {
15         if(check(val)) 
16             cnt ++;
17         if(cnt == 2019) break;
18         val++;
19     }
20     printf("%d\n", val);
21     return 0;
22 }

D.质数

答案：17569

E.最大降雨量

【问题描述】
由于沙之国长年干旱，法师小明准备施展自己的一个神秘法术来求雨。
这个法术需要用到他手中的49 张法术符，上面分别写着1 至49 这49 个数字。法术一共持续7 周，每天小明都要使用一张法术符，法术符不能重复使用。
每周，小明施展法术产生的能量为这周7 张法术符上数字的中位数。法术施展完7 周后，求雨将获得成功，降雨量为7 周能量的中位数。
由于干旱太久，小明希望这次求雨的降雨量尽可能大，请大最大值是多少？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

思路：

如果正常按照顺序排序，那么数据将会是这样子的：
1,  2,   3 |  4 | 5,  6,  7,
8,  9,  10 | 11 | 12, 13, 14,
15, 16, 17 | 18 | 19, 20, 21,
22, 23, 24 | 25 | 26, 27, 28, 这里是第四周
29, 30, 31 | 32 | 33, 34, 35,
36, 37, 38 | 39 | 40, 41, 42,
43, 44, 45 | 46 | 47, 48, 49,
这样排序好像也还行？但是题目要求的是最大值
也就是说我们在保证每一周都比上一周大的同时，还要尽量确保第四周的值尽可能的大
要完成这样，也就得在后面几周来消耗前面的小数，如1，2，3
这样才能保证每一周的增长都是大的
从后面几周来推算
49 48 47 46 3   2  1 这样保证最后一周是最大的同时，又消耗掉了3,2,1
45 44 43 42 6   5  4 消耗掉了 6,5,4
41 40 39 38 9   8  7 消耗掉了 7 8 9
37 36 35 34 12 11 10 消耗掉了 12 11 10
33 32 31 30 15 14 13 消耗掉了 15 14 13
29 28 27 26 18 17 16 消耗掉了 18 17 16
25 24 23 22 21 20 19 消耗掉了 21 20 19
然后再把它转换过来看，因为中位数是需要升序来排的
第七周： 1  2  3 46 47 48 49
第六周:  4  5  6 42 43 44 45
第五周:  7  8  9 38 39 40 41
第四周: 10 11 12 34 35 36 37
第三周: 13 14 15 30 31 32 33
第二周: 16 17 18 26 27 28 29
第一周: 19 20 21 22 23 24 25
再按照周数来排中位数,也就是从第一周排到第七周（上面我们已经进行了排序）
22, 26, 30, 34, 39, 43, 47
这时候的中位数就是34，大于我们正常排序得到的中位数

答案：34

F.旋转

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int a[101][101];
 5 
 6 int main() {
 7     int n, m; cin >> n >> m;
 8     for(int i=1; i<=n; ++i)
 9         for(int j=1; j<=m; ++j)
10             scanf("%d", &a[i][j]);
11     for(int j=1; j<=m; ++j) {
12         for(int i=n; i>=1; --i)
13             printf("%d ", a[i][j]);
14         puts("");
15     }
16     return 0;
17 }

F.旋转

G.外卖店优先级

【题目描述】

“饱了么”外卖系统中维护着N 家外卖店，编号1~N。每家外卖店都有一个优先级，初始时(0 时刻) 优先级都为0。
每经过1 个时间单位，如果外卖店没有订单，则优先级会减少1，最低减到0；而如果外卖店有订单，则优先级不减反加，每有一单优先级加2。
如果某家外卖店某时刻优先级大于5，则会被系统加入优先缓存中；如果优先级小于等于3，则会被清除出优先缓存。
给定T 时刻以内的M 条订单信息，请你计算T 时刻时有多少外卖店在优先缓存中。
【输入格式】
第一行包含3 个整数N、M 和T。
以下M 行每行包含两个整数ts 和id，表示ts 时刻编号id 的外卖店收到一个订单
1<=N, M, T<=100000，1<=ts<=T，1<=id<=N。

【输出格式】
输出一个整数代表答案。

【输入样例】
2 6 6
1 1
5 2
3 1
6 2
2 1
6 2
【输出样例】
1

思路：按照小编号外卖店在前、小订单时间在前排序，然后遍历，针对每个店铺进行操作。将其外卖处理完成后，再与给定的时刻T判断，最后根据结果更新答案。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 struct Node { //创建结构体
 5     int ts, id;
 6 }arr[100005];
 7 
 8 int n, m, t;
 9 int ans = 0;
10 
11 bool cmp(Node &x, Node &y) {
12     if(x.id != y.id)
13         return x.id < y.id;
14     else
15         return x.ts < y.ts;
16 }
17 
18 int Read();
19 
20 int main() {
21     cin >> n >> m >> t;
22     for(int i=1; i<=m; i++) {
23         arr[i].ts = Read();
24         arr[i].id = Read();
25     }
26 
27     // 按照小编号外卖店在前 小订单时间在前 排序 
28     sort(arr+1, arr+1+m, cmp);
29     
30     for(int i=1; i<=m; ) {
31         int nowid = arr[i].id;    // 记录当前店铺的id
32         int priority = 2;        // 从该店铺被发放订单的第二个时刻开始，因此优先级初值设为了2
33         int flag = false;        // 标记是否让该店铺进入缓存
34         // 一直对当前店铺操作 
35         while(arr[++i].id == nowid) {
36             // 当前时刻与下一个不相同 需要扣除等待的优先级 
37             // 例如2 - 5时刻 需要扣除 2(5-2-1)优先级 
38             if(arr[i].ts != arr[i-1].ts)
39                 priority = priority - (arr[i].ts - arr[i-1].ts - 1);
40             if(priority < 0) priority = 0;    // 优先级不小于0 
41             if(priority <= 3) flag = false;    // 优先级小于3，则退出缓存
42             priority += 2;    // 有订单优先级+2后，再判断是否可以重新进入缓存中
43             if(priority >= 6) flag = true;    // 优先级大于6，则允许进入缓存
44         }
45         if(flag) {    // 计算进入缓存的店铺的数目
46             // 最后一个订单完成还没有到达指定时刻 
47             if(t != arr[i-1].ts)
48                 priority = priority - (t - arr[i-1].ts);
49             if(priority > 3) ans++;    // 优先级仍大于3，数量+1
50         }
51     }
52     cout<<ans<<endl;
53     return 0;
54 }
55 
56 int Read() {
57     int f = 1, x = 0;
58     char ch = getchar();
59     while(ch<'0' || ch>'9') {
60         if(ch == '-') {
61             f = -1;
62         }
63         ch = getchar();
64     }
65     while(ch>='0' && ch<='9') {
66         x = x * 10 + (ch - 48);
67         ch = getchar();
68     }
69     return x*f;
70 }

G.外卖店优先级

H.人物相关性分析

【题目描述】
小明正在分析一本小说中的人物相关性。他想知道在小说中 Alice 和 Bob 有多少次同时出现。
更准确的说，小明定义 Alice 和 Bob“同时出现”的意思是:在小说文本中 Alice 和 Bob 之间不超过 K 个字符。
例如以下文本:
This is a story about Alice and Bob. Alice wants to send a private message to Bob.
假设 K = 20，则 Alice 和 Bob 同时出现了 2 次，分别是”Alice and Bob”和”Bob. Alice”。前者 Alice 和 Bob 之间有 5 个字符，后者有 2 个字符。
注意:
1. Alice 和 Bob 是大小写敏感的，alice 或 bob 等并不计算在内。
2. Alice 和 Bob 应为单独的单词，前后可以有标点符号和空格，但是不能有字母。例如 Bobbi 并不算出现了 Bob。

【输入格式】
第一行包含一个整数 K。第二行包含一行字符串，只包含大小写字母、标点符号和空格。长度不超过 1000000。
(对于所有评测用例，1≤ K ≤1000000。)

【输出格式】
输出一个整数，表示 Alice 和 Bob 同时出现的次数

【样例输入】
20
This is a story about Alice and Bob. Alice wants to send a private message to Bob.

【样例输出】
2

思路：1.暴力。先遍历一遍找到两个独立名字的位置，分别记录下来；然后统计Alice在前和Alice在后的情况。超时。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 //  TLE
 5 
 6 char s[1000010];
 7 int lenA, lenB, K, Ans ;
 8 int A[501010], B[501010];
 9 
10 bool check(int pos, int x) {
11     char ch;
12     if(pos!=0) {
13 //        前一个是字母
14         ch = s[pos-1];
15         if((ch>='A'&&ch<='Z') || (ch>='a'&&ch<='z')) {
16             return false;
17         }
18     }
19 //    后一个 
20     ch = s[pos+x];
21     if((ch>='A'&&ch<='Z') || (ch>='a'&&ch<='z')) {
22         return false;
23     }
24     return true;
25 }
26 
27 int main() {
28     cin >> K;
29     getchar(); 
30     gets(s);
31     int len = strlen(s);
32     for(int i=0; i<len; ++i) {
33         if(s[i] == 'A') {
34             if(check(i, 5)) 
35                 A[++lenA] = i;
36         }
37         else if(s[i] == 'B') {
38             if(check(i, 3)) 
39                 B[++lenB] = i;
40         }
41     }
42     
43     for(int i=1; i<=lenA; ++i) {
44         for(int j=1; j<=lenB; ++j) {
45             if(A[i] > B[j]) continue;
46             int p1 = A[i] + 4 + 1;
47             if(B[j]-p1 <= K) {
48                 Ans++;
49             }
50             else break;
51         }
52     }
53 
54     for(int i=1; i<=lenB; ++i) {
55         for(int j=1; j<=lenA; ++j) {
56             if(B[i] > A[j]) continue;
57             int p1 = B[i] + 2 + 1;
58             if(A[j]-p1 <= K) Ans++;
59             else break;
60         }
61     }
62     printf("%d", Ans);
63 //    for(int i=1; i<=lenA; ++i) printf("A: %d\n", A[i]);
64 //    for(int i=1; i<=lenB; ++i) printf("B: %d\n", B[i]);
65     return 0;
66 }

H.人物相关性分析-暴力-超时

2.滑动窗口。由方法1考虑到最后统计Alice在前和Alice在后的情况可以同时进行，省下约一半的时间。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 char s[1000010];
 5 int lenA, lenB, K;
 6 int A[1001010], B[1001010];
 7 long long Ans; 
 8 
 9 bool check(int pos, int x) {
10     char ch;
11     if(pos!=0) {
12 //        前一个是字母
13         ch = s[pos-1];
14         if((ch>='A'&&ch<='Z') || (ch>='a'&&ch<='z')) {
15             return false;
16         }
17     }
18 //    后一个 
19     ch = s[pos+x];
20     if((ch>='A'&&ch<='Z') || (ch>='a'&&ch<='z')) {
21         return false;
22     }
23     return true;
24 }
25 
26 int main() {
27     cin >> K;
28     getchar(); 
29     gets(s);
30     int len = strlen(s);
31     for(int i=0; i<len; ++i) {
32         if(s[i] == 'A') {
33             if(check(i, 5)) 
34                 A[++lenA] = i;
35         }
36         else if(s[i] == 'B') {
37             if(check(i, 3)) 
38                 B[++lenB] = i;
39         }
40     }
41     
42     int bl = 1, br = 1;    // 滑动窗口左右边界 
43     for(int i=1; i<=lenA; ++i) {
44         int len1 = A[i]-K-3, len2 = A[i]+K+5;
45         while(bl<=lenB && B[bl]< len1) bl++;    // 维护左边界 
46         while(br<=lenB && B[br]<=len2) br++;    // 维护右边界 
47         Ans += br - bl; 
48     }
49     printf("%lld\n", Ans);
50 //    for(int i=1; i<=lenA; ++i) printf("A: %d\n", A[i]);
51 //    for(int i=1; i<=lenB; ++i) printf("B: %d\n", B[i]);
52     return 0;
53 }

H.人物相关性分析-滑动窗口-AC

I.等差数列

【题目描述】
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中 N 个整数。
现在给出这 N 个整数，小明想知道包含这 N 个整数的最短的等差数列有几项?

【输入格式】
输入的第一行包含一个整数 N。第二行包含N个整数A1,A2,···,AN。(注意A1 ～AN并不一定是按等差数列中的顺序给出)
(对于所有评测用例，2≤ N ≤100000，0≤ Ai ≤109。)

【输出格式】
输出一个整数表示答案

【样例输入】
5
2 6 4 10 20

【样例输出】
10

【样例说明】
包含2、6、4、10、20的最短的等差数列是2、4、6、8、10、12、14、16、18、20。

思路：假设最短的等差数列由X项，则有X = (An - A1) / d。所以若想X最小，则d要尽可能的大。所以d取他们这几项的公差中的最大公约数。

为什么是最大的公约数？假设数列A等差为d，任意两个数之差为val(i)，如val(1) = A2 - A1、val(2) = A3 - A1 ... 。很显然val中的每个数都是d的整倍数。所以n-1个差值的最大公约数就是我们所求的最大公差，(An - A1)/d(max) + 1就是最短的长度。特殊情况为n个整数相同，即所求差值均为0，则该数列为常数列，最短的长度就是n。

不明白的可以自己写两个数列自己比划一下。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 const int MAXN = 100000+10;
 5 
 6 int n, d;
 7 int A[MAXN]; 
 8 int val[MAXN]; 
 9 
10 // gcd
11 int gcd(int x, int y) {
12     return y? gcd(y, x%y) : x;
13 }
14 
15 int main() {
16     cin >> n;
17     // 输入并排序  
18     for(int i=0; i<n; ++i) scanf("%d", &A[i]);
19     sort(A, A+n);
20     // 求差值
21     for(int i=0; i<n-1; ++i) val[i] = A[i+1] - A[i];
22     // 求差值的最大公约数 
23     int d = gcd(val[0], val[1]);
24     for(int i=2; i<n-1; ++i) d = gcd(d, val[i]);
25     
26     // 特判公差为0
27     if(d == 0) cout << n;
28     else cout << (A[n-1] - A[0]) /  d + 1;
29     return 0;
30 }

I.等差数列

J.扫地机器人

思路：用二分法找到一个值x，其表示每个机器人所需要打扫的区域。同时设置一个数tot，表示到第i-1个机器人所能打扫的总区域。而对于每一个机器人k[i]都有：

1. k[i] < total: 说明前面一个机器人k[i - 1]能够清扫的右边界达到k[i]的起始位置，那么第i个机器人就不用往左边走了，此时前i个机器人能够清扫的total = k[i] + x - 1；
2. k[i] >= total: 说明前面一个机器人k[i - 1]能够清扫的右边界没有达到k[i]的起始位置，那么第i个机器人就需要往左边清扫，而此时前i个机器人能够清扫的total = total + x；
如果 k[i] - x > total 的话，也就是第 i 个机器人能够清扫的左边界都大于前 i - 1 个机器人能够清扫到的范围，那说明这个 x 选的太小了，得增大范围。

最后找到了合适的 x 之后，那么花费时间最长的机器人，就是这个机器人的位置正好在 x 的中间，它需要先往左扫，再回来，然后往右扫，再回来，所以花费的最长时间为 (x - 1) * 2。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 const int MAXN = 1e5 + 10;
 5 int n, m;
 6 int robotList[MAXN];
 7 
 8 bool check(int x) {
 9     int total = 0;
10     for (int i = 0; i < m; i++) {
11         if (robotList[i] - x < total + 1) {
12             if (robotList[i] < total + 1) {
13                 total = robotList[i] + x - 1;
14             } else {
15                 total += x;
16             }
17         } else {
18             return false;
19         }
20     }
21     return total > n - 1;
22 }
23 
24 int main() {
25     
26     cin >> n >> m;
27     for (int i = 0; i < m; i++) cin >> robotList[i];
28     sort(robotList, robotList + m);    
29     
30     int left = 0, right = n, middle, ans;
31     while (left < right + 1) {
32         middle = (right + left) >> 1;
33         if (check(middle)) {
34             right = middle - 1;
35             ans = middle;
36         } else {
37             left = middle + 1;
38         }
39     }
40     cout << (ans - 1) * 2 << endl;
41     return 0;
42 }

J.扫地机器人

posted on 2023-04-17 18:35 Marginalin 阅读(144) 评论(0) 编辑收藏举报

刷新页面返回顶部

Marginalin