2019-第十届蓝桥杯大赛个人赛省赛(软件类)真题 C大学B组
题目一览:
A.组队
B.年号字串
C. 数列求值
D.数的分解
E.迷宫
F.特别数的和
G.完全二叉树的权值
H.等差数列
I.后缀表达式
J.灵能传输
A.组队
【题目描述】
作为篮球队教练,你需要从以下名单中选出1 号位至5 号位各一名球员,组成球队的首发阵容。
每位球员担任1号位至5号位时的评分如下表所示。请你计算首发阵容1号位至5号位的评分之和最大可能是多少?

1 97 90 0 0 0 2 92 85 96 0 0 3 0 0 0 0 93 4 0 0 0 80 86 5 89 83 97 0 0 6 82 86 0 0 0 7 0 0 0 87 90 8 0 97 96 0 0 9 0 0 89 0 0 10 95 99 0 0 0 11 0 0 96 97 0 12 0 0 0 93 98 13 94 91 0 0 0 14 0 83 87 0 0 15 0 0 98 97 98 16 0 0 0 93 86 17 98 83 99 98 81 18 93 87 92 96 98 19 0 0 0 89 92 20 0 99 96 95 81
思路:每个位置选择一个最大的评分,然后加起来。
答案:490
B.年号字串
【问题描述】
小明用字母A 对应数字1,B 对应2,以此类推,用Z 对应26。对于27以上的数字。
小明用两位或更长位的字符串来对应,例如AA 对应27,AB 对应28,AZ 对应52,LQ 对应329。
请问2019 对应的字符串是什么?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:1. 应该很容易看出这就是Excel的编号方式,所以最简单的就是用Excel啦。
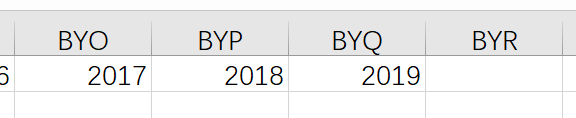
2. 很明显逢27进一位,直接模拟。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int main() { 5 long long x, y, len=0; 6 char s[101]; 7 // scanf("%lld", &x); 8 x = 2019; 9 while(x) { 10 y = x % 26; 11 x /= 26; 12 if(!y) y = 26, x--; 13 s[++len] = 'A' + y - 1; 14 } 15 while(len){ 16 printf("%c", s[len--]); 17 } 18 return 0; 19 } 20 // BYQ
答案:BYQ
C.数列求值
【问题描述】
给定数列1, 1, 1, 3, 5, 9, 17, …,从第4 项开始,每项都是前3 项的和。求第20190324 项的最后4 位数字。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个4 位整数(提示:答案的千位不为0),在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路:边求和边取余。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int main() { 5 int a = 1, b = 1, c = 1; 6 for(int i=4; i<=20190324; ++i) { 7 int t = (a + b + c) % 10000; 8 a = b; b = c; c = t; 9 } 10 cout << c << endl; 11 return 0; 12 }
答案:4659
D.数的分解
【题目描述】
把2019分解成3个各不相同的正整数之和,并且要求每个正整数都不包含数字2和4,一共有多少种不同的分解方法?
注意交换3个整数的顺序被视为同一种方法,例如1000+1001+18 和1001+1000+18 被视为同一种。
思路:假设三个数分别为i, j, k。由交换顺序视为同一种方法可以得到i<j<k。可得i、j从1枚举到2019, k=2019-i-j。再判断一下三个数有没有2、4即可。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int Ans; 5 6 int check(int x) { 7 while(x) { 8 int tmp = x % 10; 9 if(tmp == 2) return false; 10 if(tmp == 4) return false; 11 x = x / 10; 12 } 13 return true; 14 } 15 16 int main() { 17 for(int i=1; i<=2019; ++i) { 18 for(int j=1; j<=2019; ++j) { 19 int k = 2019 - i - j; 20 if(i<j && j<k) { 21 if(check(i)) { 22 if(check(j)) { 23 if(check(k)) { 24 Ans ++; 25 } 26 } 27 } 28 } 29 } 30 } 31 cout << Ans; 32 return 0; 33 }
答案:40785
E.迷宫
【问题描述】
下图给出了一个迷宫的平面图,其中标记为1 的为障碍,标记为0 的为可
以通行的地方。
010000 000100 001001 110000
迷宫的入口为左上角,出口为右下角,在迷宫中,只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫,从入口开始,可以按DRRURRDDDR 的顺序通过迷宫,一共10 步。其中D、U、L、R 分别表示向下、向上、向左、向右走。
对于下面这个更复杂的迷宫(30 行50 列),请找出一种通过迷宫的方式,其使用的步数最少,在步数最少的前提下,请找出字典序最小的一个作为答案。
请注意在字典序中D<L<R<U。(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件maze.txt,内容与下面的文本相同)
01010101001011001001010110010110100100001000101010 00001000100000101010010000100000001001100110100101 01111011010010001000001101001011100011000000010000 01000000001010100011010000101000001010101011001011 00011111000000101000010010100010100000101100000000 11001000110101000010101100011010011010101011110111 00011011010101001001001010000001000101001110000000 10100000101000100110101010111110011000010000111010 00111000001010100001100010000001000101001100001001 11000110100001110010001001010101010101010001101000 00010000100100000101001010101110100010101010000101 11100100101001001000010000010101010100100100010100 00000010000000101011001111010001100000101010100011 10101010011100001000011000010110011110110100001000 10101010100001101010100101000010100000111011101001 10000000101100010000101100101101001011100000000100 10101001000000010100100001000100000100011110101001 00101001010101101001010100011010101101110000110101 11001010000100001100000010100101000001000111000010 00001000110000110101101000000100101001001000011101 10100101000101000000001110110010110101101010100001 00101000010000110101010000100010001001000100010101 10100001000110010001000010101001010101011111010010 00000100101000000110010100101001000001000000000010 11010000001001110111001001000011101001011011101000 00000110100010001000100000001000011101000000110011 10101000101000100010001111100010101001010000001000 10000010100101001010110000000100101010001011101000 00111100001000010000000110111000000001000000001011 10000001100111010111010001000110111010101101111000
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个字符串,包含四种字母D、U、L、R,在提交答案时只填写这个字符串,填写多余的内容将无法得分。
思路:
1. 将迷宫放到excel里面,标记一下障碍的格子,就可以手动模拟了。但要细心哦。效果如下:

2. 老老实实的打一遍BFS

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int n, m; 5 int u[4] = {1, 0, 0, -1}, 6 v[4] = {0, -1, 1, 0}; 7 int dxy[] = {'D','L','R','U'}; 8 int Map[31][51]; 9 int vis[31][51]; 10 int head, tail; 11 struct Node { 12 int x, y, f, sum; // xy坐标 f从该节点过来 sum步数 13 char c; // 方向 14 }que[1505]; 15 16 void print(int index) { 17 if(index == 0) { 18 return; 19 } 20 21 print(que[index].f); 22 cout << que[index].c; 23 24 } 25 26 bool check(int x, int y) { 27 if(x <= 0) return false; 28 if(x > 30) return false; 29 if(y <= 0) return false; 30 if(y > 50) return false; 31 if(Map[x][y] != 0) return false; 32 if(vis[x][y] != 0) return false; 33 return true; 34 } 35 void bfs() 36 { 37 que[0].x = que[0].y = 1; // 初始坐标 38 que[0].sum = 0; // 初始步数 39 vis[1][1] = 1; // 标记已经访问 40 tail = 1; 41 while(head < tail) { 42 // 找到终点 打印路径 43 if(que[head].x==30 && que[head].y==50) { 44 print(head); 45 return ; 46 } 47 // 四个方向搜索 48 for(int i=0; i<4; i++) { 49 int dx = que[head].x + u[i]; // 获取下一个坐标 50 int dy = que[head].y + v[i]; 51 // 没出界 不是障碍 未访问 添加进来 52 if(check(dx, dy)) { 53 vis[dx][dy] = 1; 54 que[tail].x = dx; 55 que[tail].y = dy; 56 que[tail].f = head; 57 que[tail].c = dxy[i]; 58 que[tail].sum = que[head].sum + 1; 59 tail++; 60 } 61 } 62 head++; 63 } 64 65 } 66 int main() 67 { 68 for(int i=1;i<=30;i++) { 69 for(int j=1;j<=50;j++) { 70 scanf("%1d", &Map[i][j]); 71 } 72 } 73 bfs(); 74 return 0; 75 }
答案:
DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR
F.特别数的和
【题目描述】
小明对数位中含有2、0、1、9 的数字很感兴趣(不包括前导0)
在1到40中这样的数包括1、2、9、10 至32、39 和40,共28 个,他们的和是574。
请问,在1到n 中,所有这样的数的和是多少?
【输入格式】
输入一个正整数n(1<=n<=10000)
【输出格式】
输出一行,包含一个整数,表示满足条件的数的和。
【样例输入】
40
【样例输出】
574
思路:遍历一遍 然后判断有没有2、0、1、9。有的话加起来即可。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int n; 5 long long sum = 0; 6 7 bool check(int x) { 8 while(x) { 9 int tmp = x % 10; 10 x = x / 10; 11 if(tmp == 2) return true; 12 if(tmp == 0) return true; 13 if(tmp == 1) return true; 14 if(tmp == 9) return true; 15 } 16 return false; 17 } 18 19 int main() { 20 cin >> n; 21 for(int i=1; i<=n; ++i) 22 if(check(i)) 23 sum += i; 24 cout << sum; 25 return 0; 26 }
G.完全二叉树的权值
【问题描述】
给定一棵包含N 个节点的完全二叉树,树上每个节点都有一个权值,按从上到下、从左到右的顺序依次是A1, A2, AN,如下图所示:
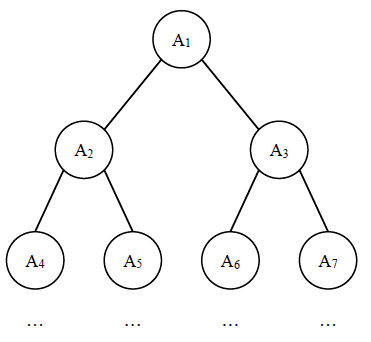
现在小明要把相同深度的节点的权值加在一起,他想知道哪个深度的节点权值之和最大?如果有多个深度的权值和同为最大,请你输出其中最小的深度。
注:根的深度是1。
【输入格式】
第一行包含一个整数N。
第二行包含N 个整数A1, A2, AN
对于所有评测用例,1<=N<=100000, -100000<=Ai<=100000。
【输出格式】
输出一个整数代表答案。
【输入样例】
7
1 6 5 4 3 2 1
【输出样例】
2
样例解析:

思路:可以在输入的时候用前缀和,然后求出每层的和,最后遍历一下。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int n; 5 int maxDeep; 6 int maxSum; 7 int sum[100002]; 8 9 int main() { 10 cin >> n; 11 for(int i=1; i<=n; ++i) { 12 scanf("%d", &sum[i]); 13 sum[i] += sum[i-1]; // 前缀和 14 } 15 int i, j; 16 for(i = 1, j = 1; j <= n; i++, j = (j<<1)+1) 17 sum[i] = sum[j] - sum[j >> 1]; 18 if(j > n) sum[i] = sum[n] - sum[j>>1]; //特判:最后一层,可能不满 19 20 maxSum = sum[1]; maxDeep = 1; 21 for(int j=2; j<=i; ++j) { 22 if(sum[j] > maxSum) { 23 maxSum = sum[j]; 24 maxDeep = j; 25 } 26 } 27 printf("%d\n", maxDeep); 28 return 0; 29 }
H.等差数列
【题目描述】
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列,只记得其中 N 个整数。
现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有几项?
【输入格式】
输入的第一行包含一个整数 N。 第二行包含N个整数A1,A2,···,AN。(注意A1 ~AN并不一定是按等差数列中的顺序给出)
(对于所有评测用例,2≤ N ≤100000,0≤ Ai ≤109。)
【输出格式】
输出一个整数表示答案
【样例输入】
5
2 6 4 10 20
【样例输出】
10
【样例说明】
包含2、6、4、10、20的最短的等差数列是2、4、6、8、10、12、14、16、18、20。
思路:假设最短的等差数列由X项,则有X = (An - A1) / d。所以若想X最小,则d要尽可能的大。所以d取他们这几项的公差中的最大公约数。
为什么是最大的公约数?假设数列A等差为d,任意两个数之差为val(i),如val(1) = A2 - A1、val(2) = A3 - A1 ... 。很显然val中的每个数都是d的整倍数。所以n-1个差值的最大公约数就是我们所求的最大公差,(An - A1)/d(max) + 1就是最短的长度。特殊情况为n个整数相同,即所求差值均为0,则该数列为常数列,最短的长度就是n。
不明白的可以自己写两个数列自己比划一下。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 const int MAXN = 100000+10; 5 6 int n, d; 7 int A[MAXN]; 8 int val[MAXN]; 9 10 // gcd 11 int gcd(int x, int y) { 12 return y? gcd(y, x%y) : x; 13 } 14 15 int main() { 16 cin >> n; 17 // 输入并排序 18 for(int i=0; i<n; ++i) scanf("%d", &A[i]); 19 sort(A, A+n); 20 // 求差值 21 for(int i=0; i<n-1; ++i) val[i] = A[i+1] - A[i]; 22 // 求差值的最大公约数 23 int d = gcd(val[0], val[1]); 24 for(int i=2; i<n-1; ++i) d = gcd(d, val[i]); 25 26 // 特判公差为0 27 if(d == 0) cout << n; 28 else cout << (A[n-1] - A[0]) / d + 1; 29 return 0; 30 }
I.后缀表达式
【题目描述】
给定N 个加号、M 个减号以及N + M + 1 个整数A1,A2,...,AN+M+1
小明想知道在所有由这N 个加号、M 个减号以及N + M +1 个整数凑出的合法的后缀表达式中,结果最大的是哪一个?
请你输出这个最大的结果。
例如使用1 2 3 + -,则“2 3 + 1 -” 这个后缀表达式结果是4,是最大的。
【输入格式】
第一行包含两个整数N 和M。
第二行包含N + M + 1 个整数A1,A2,...,AN+M+1
0<=N,M<=100000,-10^9<=Ai<=10^9
【输出格式】
输出一个整数,代表答案。
【样例输入】
1 1
1 2 3
【样例输出】
4
思路:
以输入A, b, c, d为例,大写表示正数,小写表示负数
sum_abs = abs(A) + abs(b) + abs(c) + abs(d);
sum_normal = A + b + c + d;
一、没有减号,即M = 0
ret = A + b + c + d;
二、减号的数量等于负数的数量,对于输入序列A, b, c, d,即M = 3
sum = A - b - c - d;
在每个负数前都加上减号,所以ret = sum_abs;
三、减号的数量小于负数的数量,对于输入序列A, b, c, d,减号M的取值为2,1
即 sum = A - b - (c + d) 或 sum = A - (b + c) - d 或 sum = A - (b + c + d)
可以得到一般情况下,ret = sum_abs;
特殊情况:
如果A改为a,即输入序列全为负数,此时减号M的取值为3,2,1
sum = a - b - c - d
或 sum = a - b - (c + d) = a - b - c - d
或 sum = a - (b + c) - d = a - b - c - d
或 sum = a - (b + c + d) = a - b - c - d
a为负数,后面的表达式结果为正数,为使ret最大,a为负数中的最大值
所以ret = sum_abs + 2 * maxum;
四、减号的数量大于负数的数量,如果输入序列为A,B,C,d,此时减号M的取值为3,2
即sum = A - (d - B - C) = A + B + C - d 或 sum = A - (d - B) + C = A - d + B + C
可以得到一般情况下,ret = sum_abs;
特殊情况:
如果d改为D,即输入序列全为正数,此时减号M的取值为3,2,1
sum = A - (B - C - D) = A - B + C + D
或 sum = A - (B - C) + D = A - B + C + D
或 sum = A - B + C + D
可以得到结果均为A - B + C + D ,此时B应为非负数的最小值,使ret最大
所以ret = sum_abs - 2 * minum;

1 #include <bits/stdc++.h> 2 using namespace std; 3 int n, m; 4 int num[200001]; 5 int negative = 0, positive = 0; 6 int minum = 1e9 + 1, maxum = -1e9 - 1; 7 8 int main(){ 9 cin >> n >> m; 10 long long sum_abs = 0, sum = 0, ret = 0; 11 for(int i = 0; i < n + m + 1; i++) { 12 cin >> num[i]; 13 if(num[i] < 0) negative++; 14 else positive++; 15 if(num[i] > maxum && num[i] < 0) maxum = num[i]; 16 if(num[i] < minum && num[i] >= 0) minum = num[i]; 17 } 18 for(int i = 0; i < n + m + 1; i++) { 19 sum_abs += abs(num[i]); 20 sum += num[i]; 21 } 22 if(negative == m) { 23 ret = sum_abs; 24 } else if(m == 0) { 25 ret = sum; 26 } else if(negative < m) { 27 if(negative == 0) { 28 ret = sum_abs - 2 * minum; 29 }else{ 30 ret = sum_abs; 31 } 32 } else { 33 if(positive == 0) { 34 ret = sum_abs + 2 * maxum; 35 } else { 36 ret = sum_abs; 37 } 38 } 39 cout << ret << endl; 40 return 0; 41 }
参考:[蓝桥杯2019初赛]后缀表达式_Agcl无悔的博客-CSDN博客
J.灵能传输




3 5 6 -4 2 -7 3 10 -99 -53 43 80 -83 72 99 78 -63 -9 100 373837389 225627048 -847064399 487662607 579717002 903937892 -89313283 134706789 259978604 399131737 298183518 62083619 -444218530 403702220 358088455 -973959249 -637339048 -736509394 -552801709 -98262597 -532577703 -393599463 762744971 -683270041 716127816 -991756495 734780346 27919355 -421469435 258728334 844409214 -270792553 -490888330 133696186 843888283 -35439761 -73481392 -118968548 269164182 978558860 522378250 -979427259 -330256906 235192566 -652699569 -708569352 -778693386 241745676 583226906 121065292 -503683097 599394257 405122877 437067802 238539735 -957745973 -843677563 -690555937 908484805 940157941 524765035 730436972 -17856720 -530595388 -727773574 617781285 491720304 -779040285 -298295760 -699402143 230749576 404009775 126806094 -140842651 198136484 681875881 997449600 898972467 -239590302 -62193410 866009412 -401154712 -276085482 593177187 -236793216 487533624 75511548 -446699920 -869912037 -330666015 268937148 -430325605 -635949275 361887555 -855294881 87004526 782523543 -69083645 -965396597 -880697065

5 88 381470940
参考:蓝桥杯:2019年第十届蓝桥杯省赛B组试题J — 灵能传输_异能传输题目_Belous的博客-CSDN博客
posted on 2023-04-17 18:26 Marginalin 阅读(300) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号