2017-第八届蓝桥杯大赛个人赛省赛（软件类）真题 C大学C组

题目一览：

1.贪吃蛇长度

+-------------------------------------------------+
|                                                 |
|    H######                      ####            |
|          #                      #  #            |
|          #                      #  #            |
|          #     ####             #  #            |
|          #     #  #             #  #            |
|          ######@###             #  #            |
|                #       ####     #  #            |
|                #       #  #     #  #            |
|            ####@#######@###     #  #            |
|            #   #       #        #  #            |
| T          #####       #        #  #   ##       |
| #                      #      ###  ### ##       |
| ################       #      #      ####       |
|                #       #      #         #       |
|   ##############       #######@##########       |
|   #                         ###                 |
|   ###########################                   |
+-------------------------------------------------+

小明在爷爷的私人收藏馆里找到一台老式电脑。居然没有图形界面，只能用控制台编程。
经过小明的一阵摸索，神奇地设计出了控制台上的贪食蛇游戏。

如上图，是游戏时画面截图。
其中，H表示蛇头，T表示蛇尾。#表示蛇的身体，@表示身体交叉重叠的地方。
你能说出现在的贪吃蛇长度是多少吗？

其实，只要数出#的数目算1，数出@的数目，算2，再加上头尾各算1就计算好了。

人工数一下？太累眼睛了，聪明的你为什么不让计算机帮忙呢？

本题的要求就是：请填写上图中贪食蛇的长度是多少？

注意：需要提交的是一个整数，不要添加任何多余内容（比如说明或注释）

思路：读取挨个判断就好。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 char s[21][666];
 5 int Ans;
 6 
 7 int main() {
 8     for(int i=0; i<20; ++i) gets(s[i]);
 9     for(int i=0; i<20; ++i) {
10         for(int j=0; j<51; ++j) {
11             if(s[i][j] == '#') Ans ++;
12             else if(s[i][j] == '@') Ans += 2;
13         }
14     }
15     Ans += 2;
16     printf("%d", Ans);
17     return 0;
18 }

1.贪吃蛇长度

答案：190

2.兴趣小组

为丰富同学们的业余文化生活，某高校学生会创办了3个兴趣小组
（以下称A组，B组，C组）。
每个小组的学生名单分别在【A.txt】,【B.txt】和【C.txt】中。
每个文件中存储的是学生的学号。

12894792, 92774113, 59529208, 22962224, 02991600, 83340521, 87365045, 
40818286, 16400628, 39475245, 55933381, 76940287, 61366748, 95631228, 
17102313, 50682833, 61562613, 87002524, 83062019, 51743442, 61977890, 
32010762, 69680621, 87179571, 81761697, 32364296, 07833271, 36198035, 
26588918, 84046668, 43059468, 73191775, 56794101, 00454780, 11141030, 
10008994, 35072237, 44945158, 53959980, 75758119, 18560273, 35801494, 
42102550, 22496415, 03981786, 34593672, 13074905, 07733442, 42374678, 
23452507, 98586743, 30771281, 17703080, 52123562, 05898131, 56698981, 
90758589, 18238802, 18217979, 04511837, 75682969, 31135682, 55379006, 
42224598, 98263070, 40228312, 28924663, 11580163, 25686441, 45944028, 
96731602, 53675990, 03854194, 14858183, 16866794, 40677007, 73141512, 
32317341, 56641725, 43123040, 15201174, 62389950, 72887083, 76860787, 
61046319, 06923746, 17874548, 46028629, 10577743, 48747364, 05328780, 
59855415, 60965266, 20592606, 14471207, 70896866, 46938647, 33575820, 
53426294, 56093931, 51326542, 94050481, 80114017, 33010503, 72971538, 
22407422, 17305672, 78974338, 93209260, 83461794, 41247821, 26118061, 
10657376, 42198057, 15338224, 50284714, 32232841, 26716521, 76048344, 
23676625, 62897700, 69296551, 59653393, 38704390, 48481614, 69782897, 
26850668, 37471053, 88720989, 51010849, 94951571, 60024611, 29808329, 
70377786, 13899299, 09683688, 58218284, 46792829, 97221709, 45286643, 
48158629, 57367208, 26903401, 76900414, 87927040, 09926730, 01508757, 
15101101, 62491840, 43802529,

A.txt

44894050, 34662733, 44141729, 92774113, 99208727, 91919833, 23727681, 
10003409, 55933381, 54443275, 13584702, 96523685, 50682833, 61562613, 
62380975, 20311684, 93200452, 23101945, 42192880, 28992561, 18460278, 
19186537, 58465301, 01111066, 62680429, 23721241, 20277631, 91708977, 
57514737, 03981786, 81541612, 07346443, 93154608, 19709455, 37446968, 
17703080, 72378958, 66200696, 30610382, 89586343, 33152171, 67040930, 
35696683, 63242065, 99948221, 96233367, 52593493, 98263070, 01418023, 
74816705, 89375940, 58405334, 96731602, 84089545, 16866794, 94737626, 
01673442, 70548494, 13638168, 08163691, 11106566, 64375392, 40267902, 
00897705, 56447313, 54532235, 94738425, 66642634, 83219544, 40546096, 
66924991, 20592606, 96037590, 73434467, 70896866, 91025618, 57892091, 
08487641, 32500082, 84412833, 23311447, 38380409, 79957822, 72971538, 
69645784, 91863314, 73099909, 93209260, 83461794, 81378487, 30423273, 
22233715, 32232841, 26716521, 03511221, 29196547, 58263562, 56233305, 
52547525, 55812835, 87253244, 52484232, 80837360, 94098464, 52028151, 
53267501, 66381929, 84381316, 59788467, 09683688, 67082008, 71605255, 
80654064, 21434307, 45286643, 76556656, 82465821, 57367208, 79218980, 
48460468, 59170479, 46046391, 43043164, 96544490, 83340521, 70837892, 
18926791, 40818286, 28936302, 11489524, 51031183, 73860337, 13241219, 
09025448, 10718828, 76360986, 26031606, 76558053, 97726139, 46473415, 
48406387, 23625539, 86756012, 35164187, 49161302, 78082834, 35072237, 
08602486, 29815841, 56562216, 77684187, 81751704, 20160464, 50407962, 
27786415, 19893526, 00934129, 37759498, 52636463, 25666982, 43262852, 
38393436, 02581136, 29323250, 56950657, 05898131, 95286262, 75574581, 
54057961, 06703896, 90758589, 57782642, 34492535, 41919697, 06395464, 
10993500, 81212949, 34017532, 69569396, 99009936, 57129610, 67401593, 
71044018, 62076698, 29533873, 71936325, 86874388, 26545032, 35695544, 
30433724, 53127345, 72887083, 25390873, 63711546, 06923746, 27783723, 
33199575, 35929698, 16491251, 18276792, 62744775, 92096155, 06336570, 
56141974, 73007273, 31416832, 00171057, 64176982, 46938647, 58460388, 
69972026, 73724304, 27435484, 51568616, 15531822, 47788699, 11818851, 
41594694, 83561325, 43107163, 56965375, 10557343, 26118061, 74650126, 
90076467, 10657376, 49901436, 03425162, 61164599, 15797769, 05427896, 
14444084, 36795868, 18079449, 59653393, 72942548, 06763077, 33895610, 
94892653, 12085268, 65174140, 79567366, 23020126, 74290047, 13498869, 
21696323, 27724594, 54941003, 38229841, 07050068,

B.txt

13404901, 39952424, 47847739, 94939581, 13809950, 70966043, 11161555, 
17102313, 47079425, 50682833, 74154313, 61562613, 93200452, 37103342, 
18479435, 32502597, 36198035, 54210010, 73191775, 48358178, 85544503, 
05996766, 54651623, 52113220, 27465181, 23871783, 22496415, 54107041, 
65899605, 56528700, 82671109, 61176034, 42374678, 51612628, 63329997, 
56591652, 04552733, 12789324, 89586343, 51935014, 38611966, 43916409, 
70996050, 98263070, 01418023, 65345049, 21734275, 76846198, 71506230, 
00833171, 67128139, 41367555, 64769510, 44010700, 16475199, 93164325, 
09386162, 95324041, 80688223, 67629139, 79552617, 76219736, 50368644, 
45096021, 54972488, 63779011, 28862942, 73145521, 74078605, 66924991, 
12806850, 02171001, 70896866, 73434467, 08487641, 44415025, 32500082, 
84412833, 83896188, 52243759, 49191410, 38744339, 48079796, 44937032, 
06267501, 81866886, 38575984, 25978688, 78974338, 41247821, 12356966, 
64842303, 79127158, 02366944, 68000570, 12426275, 96409230, 00705972, 
08266503, 83820884, 08831807, 43273308, 23216105, 29196547, 95160161, 
05553537, 52182214, 32641346, 91553427, 24436506, 77433749, 01979664, 
52028151, 88985343, 01761499, 76203088, 63237368, 23405334, 59788467, 
09683688, 67755443, 29946533, 12053603, 00437479, 15200030, 45286643, 
93537527, 82465821, 57367208, 53899751, 15354933, 97760830, 68933762, 
80220545, 01892750, 39868288, 21524323, 69716610, 65083815, 78048499, 
03227391, 83340521, 87365045, 71720254, 51031183, 89168555, 08503028, 
37086236, 25103057, 87002524, 22808816, 80928090, 90741678, 15993372, 
99117082, 49938176, 21755083, 86903426, 87830263, 53959980, 75758119, 
59781354, 58679691, 25666982, 56307643, 47180521, 62776522, 78136608, 
44882734, 90758589, 08075999, 66303819, 23480347, 11580163, 87080118, 
18329165, 92514163, 89404632, 92377859, 03912329, 17499963, 59699979, 
79876366, 63894807, 37857001, 86003935, 90087123, 29433345, 80298948, 
61531153, 61046319, 37839841, 19421134, 48747364, 35196916, 62484573, 
59907079, 36845702, 21631642, 72739317, 26283700, 80114017, 76639390, 
29154110, 35159758, 47788699, 11818851, 56520669, 36396767, 36031167, 
83817428, 10657376, 90076467, 14676452, 11024560, 16327605, 76048344, 
14444084, 95452011, 99612346, 65172562, 84813675, 88618282, 38704390, 
27998014, 63859011, 33787505, 60024611, 16229880, 13899299, 35240335, 
29173227, 45036451, 66177893, 82658333, 43100730, 44520187, 74290047, 
85013538, 09926730, 27724594, 95148523, 20503000, 64390907, 26006953, 
98116293, 97457666, 29017396, 04634371, 70791589,

C.txt

由于工作需要，我们现在想知道：
既参加了A组，又参加了B组，但是没有参加C组的同学一共有多少人？

请你统计该数字并通过浏览器提交答案。

注意：答案是一个整数，不要提交任何多余的内容。

--------------------

笨笨有话说：
哇塞！数字好多啊！一眼望过去就能发现相同的，好像没什么指望。
不过，可以排序啊，要是每个文件都是有序的，那就好多了。

歪歪有话说：
排什么序啊，这么几行数字对计算机不是太轻松了吗？
我看着需求怎么和中学学过的集合很像啊.....

思路：读入三个小组的数据存放在三个数组里面，然后枚举

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 
 4 int A[501], B[501], C[501];
 5 int Len1, Len2, Len3, Ans;
 6 
 7 int main() {
 8     // 读入三个小组的数据，分别放到ABC三个数组内 
 9     int x;
10     freopen("A.txt", "r", stdin);
11     while(~scanf("%d, ", &x)) {
12         A[++Len1] = x;
13     }
14     fclose(stdin);
15     freopen("B.txt", "r", stdin);
16     while(~scanf("%d, ", &x)) {
17         B[++Len2] = x;
18     }
19     fclose(stdin);
20     freopen("C.txt", "r", stdin);
21     while(~scanf("%d, ", &x)) {
22         C[++Len3] = x;
23     }
24     fclose(stdin);
25     //printf("--------------------------\n");
26     int i, j, k;
27     for(i=1; i<=Len1; ++i) {
28         for(j=1; j<=Len2; ++j) {
29             int flag = 1; // 假设不在C组 
30             if(A[i] == B[j]) { // 参加A和B 
31                 for(k=1; k<=Len3; ++k) 
32                 if(A[i] == C[k]) { // C组有他，标记退出 
33                     flag = 0;
34                     break;
35                 }
36                 if(flag) Ans ++; // 不在C组 
37             }
38         }
39     }
40     printf("%d\n", Ans);
41     return 0;
42 }

2.兴趣小组

答案：20

3.算式900

小明的作业本上有道思考题：

看下面的算式：

(□□□□-□□□□)*□□=900

其中的小方块代表0~9的数字，这10个方块刚好包含了0~9中的所有数字。
注意：0不能作为某个数字的首位。

小明经过几天的努力，终于做出了答案！如下：
(5012-4987)*36=900

用计算机搜索后，发现还有另外一个解，本题的任务就是：请你算出这另外的一个解。

注意：提交的格式需要与示例严格一致；
括号及运算符号不要用中文输入法；
整个算式中不能包含空格。

注意：机器评卷，不要填写任何多余的内容，比如说明文字。

思路：其实是特殊一点的全排列问题，即第1、5、9位不能是0，可用dfs将十个空填好，然后判断是否符合算式。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int a[11];
 5 bool vis[11];
 6 
 7 void dfs(int pos) {
 8     if(pos > 10) { // 十个都搜完了  判断是否满足条件 
 9         int x = a[1]*1000 + a[2]*100 + a[3]*10 + a[4];
10         int y = a[5]*1000 + a[6]*100 + a[7]*10 + a[8];
11         int z = a[9]*10 + a[10];
12         int i;
13         //for(i=1; i<=10; ++i) printf("%d ", a[i]); printf("\n");
14         if((x - y)*z == 900) // 找到解 输出 
15             printf("(%d-%d)*%d=900\n", x, y, z);
16     }
17     for(int i=0; i<=9; ++i) { // 开始尝试将数填入第pos位
18         if(vis[i] == 0) {
19             if(i == 0) // 首位不能为零 
20                 if(pos==1 || pos==5 || pos==9) continue;
21             a[pos] = i; // 可以填入 将其填入 
22             vis[i] = true; // 标记已经使用 
23             dfs(pos+1); // 开始搜下一位 
24             a[pos] = -1; // 回溯 
25             vis[i] = false;
26         }
27     }
28 }
29 
30 int main() {
31     // 标记数字未使用 
32     for(int i=0; i<=9; ++i) vis[i] = false;
33     dfs(1); // 从第一位开始填入 
34     return 0;
35 }

3.算式900

答案：

(6048-5973)*12=900

4.承压计算

X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。

每块金属原料的外形、尺寸完全一致，但重量不同。
金属材料被严格地堆放成金字塔形。

 1                              7 
 2                             5 8 
 3                            7 8 8 
 4                           9 2 7 2 
 5                          8 1 4 9 1 
 6                         8 1 8 8 4 1 
 7                        7 9 6 1 4 5 4 
 8                       5 6 5 5 6 9 5 6 
 9                      5 5 4 7 9 3 5 5 1 
10                     7 5 7 9 7 4 7 3 3 1 
11                    4 6 4 5 5 8 8 3 2 4 3 
12                   1 1 3 3 1 6 6 5 5 4 4 2 
13                  9 9 9 2 1 9 1 9 2 9 5 7 9 
14                 4 3 3 7 7 9 3 6 1 3 8 8 3 7 
15                3 6 8 1 5 3 9 5 8 3 8 1 8 3 3 
16               8 3 2 3 3 5 5 8 5 4 2 8 6 7 6 9 
17              8 1 8 1 8 4 6 2 2 1 7 9 4 2 3 3 4 
18             2 8 4 2 2 9 9 2 8 3 4 9 6 3 9 4 6 9 
19            7 9 7 4 9 7 6 6 2 8 9 4 1 8 1 7 2 1 6 
20           9 2 8 6 4 2 7 9 5 4 1 2 5 1 7 3 9 8 3 3 
21          5 2 1 6 7 9 3 2 8 9 5 5 6 6 6 2 1 8 7 9 9 
22         6 7 1 8 8 7 5 3 6 5 4 7 3 4 6 7 8 1 3 2 7 4 
23        2 2 6 3 5 3 4 9 2 4 5 7 6 6 3 2 7 2 4 8 5 5 4 
24       7 4 4 5 8 3 3 8 1 8 6 3 2 1 6 2 6 4 6 3 8 2 9 6 
25      1 2 4 1 3 3 5 3 4 9 6 3 8 6 5 9 1 5 3 2 6 8 8 5 3 
26     2 2 7 9 3 3 2 8 6 9 8 4 4 9 5 8 2 6 3 4 8 4 9 3 8 8 
27    7 7 7 9 7 5 2 7 9 2 5 1 9 2 6 5 3 9 3 5 7 3 5 4 2 8 9 
28   7 7 6 6 8 7 5 5 8 2 4 7 7 4 7 2 6 9 2 1 8 2 9 8 5 7 3 6 
29  5 9 4 5 5 7 5 5 6 3 5 3 9 5 8 9 5 4 1 2 6 1 4 3 5 3 2 4 1 
30 X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X

其中的数字代表金属块的重量（计量单位较大）。
最下一层的X代表30台极高精度的电子秤。

假设每块原料的重量都十分精确地平均落在下方的两个金属块上，
最后，所有的金属块的重量都严格精确地平分落在最底层的电子秤上。
电子秤的计量单位很小，所以显示的数字很大。

工作人员发现，其中读数最小的电子秤的示数为：2086458231

请你推算出：读数最大的电子秤的示数为多少？

注意：需要提交的是一个整数，不要填写任何多余的内容。

--------------------------------------------

笨笨有话说：
不断的除2，加到下面，除2,加到下面,.... 不会浮点精度溢出吧？
歪歪有话说：
怕除不开还不好办，把每个数字扩大一定的倍数不就好了。

思路：歪歪告诉咱了。一共30层，其中第30层是秤。我们可以在读入的时候，把每个数字都乘上536870912(2^29)(30也行，但最少要29，不然到最后几行会出问题)，然后从上往下枚举，将其重量平分，分给下面两个。最后搜索一遍最后一层，也就是秤，找到最大、小值，然后用最小值除以2086458231得到一个倍数，再用最大值乘上倍数就得到了答案。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 const int Pow = 536870912;
 5 long long Map[31][31];
 6 long long Min = 9999035434, Max = -9999035434;
 7 
 8 int main() {
 9     //freopen("in.txt", "r", stdin);
10     //freopen("out.txt", "w", stdout);
11     for(int i=1; i<=29; ++i)
12         for(int j=1; j<=i; ++j) {
13             scanf("%lld", &Map[i][j]);
14             Map[i][j] *= Pow;
15         }
16     for(int i=1; i<=29; ++i) {
17         for(int j=1; j<=i; ++j) {
18             long long t = Map[i][j] / 2;
19             Map[i+1][j] += t;
20             Map[i+1][j+1] += t;
21         }
22     }
23     for(int j=1; j<=30; ++j) {
24         Max = Max>Map[30][j]? Max:Map[30][j];
25         Min = Min<Map[30][j]? Min:Map[30][j];
26     }
27     
28     long long temp = Min / 2086458231;
29     printf("%lld\n", Max/temp);
30     return 0;
31 }

4.承压计算

答案：72665192664

5.杨辉三角

杨辉三角也叫帕斯卡三角，在很多数量关系中可以看到，十分重要。

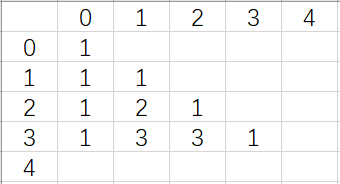
第0行： 1
第1行： 1 1
第2行： 1 2 1
第3行： 1 3 3 1
第4行： 1 4 6 4 1
....

两边的元素都是1，中间的元素是左上角的元素与右上角的元素和。

我们约定，行号，列号都从0计数。
所以：第6行的第2个元素是15，第3个元素是20

直观地看，需要开辟一个二维数组，其实一维数组也可以胜任。
如下程序就是用一维数组“腾挪”的解法。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 // 杨辉三角的第row行，第col列 
 5 long long f(int row, int col) {
 6     if(row<2) return 1;
 7     if(col==0) return 1;
 8     if(col==row) return 1;
 9 
10     long long a[1024];
11     a[0]=1;
12     a[1]=1;    
13     int p = 2;
14     int q;
15 
16     while(p<=row){
17         a[p] = 1;
18         for( _______ ) a[q] = a[q] + a[q-1]; //填空
19         p++;
20     }
21 
22     return a[col];
23 }
24 
25 int main() {
26     printf("%d\n", f(6,2));
27     printf("%d\n", f(6,3));
28     printf("%lld\n", f(40,20));    
29     return 0;
30 }

请仔细分析源码，并完成划线部分缺少的代码。
注意：只提交缺少的代码，不要提交已有的代码和符号。也不要提交说明性文字。

思路：仔细品一品10-20行。该程序的while从p=2开始，第11-12行的赋值，正是杨辉三角的第1行，所以可以推测出a数组是存放第p行的杨辉三角数。那么我们知道了第n行的数，怎么推出第n+1行呢。如下图，我们假设从第2行推第3行，那么我们首先想的是正推，也就是q从0到p-1，那么推出(3,0)的1时，a数组是{1,2,1}，看起来还挺正常，推出(3,1)的3时，a数组是{1,3,1}，看起来也没有毛病，但这时推(3,2)的3时，我们发现求出来的却是4，因原本的1+2变成了1+3，这是为什么呢，因为我们把前面的数字给改变了，2被更新成了3，但是2的职责还没有发挥完。每个数字都由他的头上还有左上角更新来的，所以某个位置没有被更新时，那么他的头上和左上的数字就不能动，这时我们考虑倒推，也就是q从p-1到0，我们发现倒推更新时只会修改头上的数字，而头上的数字更新完自己之后就没有用了，所以倒推是对的。

答案：

q=p-1; q>0; --q

6.最大公共子串

最大公共子串长度问题就是：
求两个串的所有子串中能够匹配上的最大长度是多少。

比如："abcdkkk" 和 "baabcdadabc"，
可以找到的最长的公共子串是"abcd",所以最大公共子串长度为4。

下面的程序是采用矩阵法进行求解的，这对串的规模不大的情况还是比较有效的解法。

请分析该解法的思路，并补全划线部分缺失的代码。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 #define N 256
 5 
 6 int f(const char* s1, const char* s2) {
 7     int a[N][N];
 8     int len1 = strlen(s1);
 9     int len2 = strlen(s2);
10     int i,j;
11     
12     memset(a,0,sizeof(int)*N*N);
13     int max = 0;
14     for(i=1; i<=len1; i++){
15         for(j=1; j<=len2; j++){
16             if(s1[i-1]==s2[j-1]) {
17                 a[i][j] = ____________;  //填空
18                 if(a[i][j] > max) max = a[i][j];
19             }
20         }
21     }
22     return max;
23 }
24 
25 int main() {
26     printf("%d\n", f("abcdkkk", "baabcdadabc"));
27     return 0;
28 }

注意：只提交缺少的代码，不要提交已有的代码和符号。也不要提交说明性文字。

思路：很简单的一道DP题，第16行判断当前两个字符是否相同，相同的话不就从前面转移过来嘛。

答案：

a[i-1][j-1] + 1

7.Excel地址

Excel单元格的地址表示很有趣，它使用字母来表示列号。
比如，
A表示第1列，
B表示第2列，
Z表示第26列，
AA表示第27列，
AB表示第28列，
BA表示第53列，
....

当然Excel的最大列号是有限度的，所以转换起来不难。
如果我们想把这种表示法一般化，可以把很大的数字转换为很长的字母序列呢？

本题目既是要求对输入的数字, 输出其对应的Excel地址表示方式。

例如，
输入：
26
则程序应该输出：
Z

再例如，
输入：
2054
则程序应该输出：
BZZ

我们约定，输入的整数范围[1,2147483647]

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

注意：
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <xxx>
不能通过工程设置而省略常用头文件。

提交程序时，注意选择所期望的语言类型和编译器类型。

------------------------------

笨笨有话说：
这有点像进制关系，又不完全是。好像末2位是以1当26，末3位是以1当26*26

歪歪有话说：
要是从字母序列转数字还好点，倒过来有点麻烦，不过计算机跑得快啊。

思路：首先我们能想到这就像是一个26进制数，那么我们就按照这个来写：

1     scanf("%lld", &x);
2     while(x) {
3         y = x % 26;
4         x /= 26;
5         s[++len] = 'A' + y - 1;
6     }
7     while(len){
8         printf("%c", s[len--]);
9     }

测试的时候，输入1，输出"A"，输入27，输出"AA"。看起来似乎没有什么问题，但当测试26时，发现问题了，输出的不是"Z"，而是"A@"。问题出来了，这是为什么呢。这个和进制转换还是有点区别的，因为我们的进制是逢26进一，而这个却不太是这样，因为26也是一个数，换成27进制也会出现问题，请大家自行思考。那么我们如何修改呢，我们发现当y为0时，应当输出"Z"，那么我们特判一下y为0时将其修改为26。这时再测试26，输出的是"AZ"，我们发现x没有把这个"Z"去掉。那么我们再减去1就好了。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int main() {
 5     long long x, y, len=0;
 6     char s[101];
 7     scanf("%lld", &x);
 8     while(x) {
 9         y = x % 26;
10         x /= 26;
11         if(!y) y = 26, x--;
12         s[++len] = 'A' + y - 1;
13     }
14     while(len){
15         printf("%c", s[len--]);
16     }
17     return 0;
18 }

7.Excel地址

8.九宫幻方

小明最近在教邻居家的小朋友小学奥数，而最近正好讲述到了三阶幻方这个部分，三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中，使得每一行、每一列和每一条对角线的和都是相同的。

三阶幻方又被称作九宫格，在小学奥数里有一句非常有名的口诀：“二四为肩，六八为足，左三右七，戴九履一，五居其中”，通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
4 9 2
3 5 7
8 1 6

有意思的是，所有的三阶幻方，都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小明准备将一个三阶幻方（不一定是上图中的那个）中的一些数抹掉，交给邻居家的小朋友来进行还原，并且希望她能够判断出究竟是不是只有一个解。
而你呢，也被小明交付了同样的任务，但是不同的是，你需要写一个程序~

输入格式：
输入仅包含单组测试数据。
每组测试数据为一个3*3的矩阵，其中为0的部分表示被小明抹去的部分。
对于100%的数据，满足给出的矩阵至少能还原出一组可行的三阶幻方。

输出格式：
如果仅能还原出一组可行的三阶幻方，则将其输出，否则输出“Too Many”（不包含引号）。

样例输入
0 7 2
0 5 0
0 3 0

样例输出
6 7 2
1 5 9
8 3 4

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

提交程序时，注意选择所期望的语言类型和编译器类型。

--------------

笨笨有话说：
我最喜欢这类题目了。既然九宫幻方一共也没有多少，我就不辞辛劳地一个一个写出来好了。
也不能太过分，好歹用个数组。

思路：把3*3的拉成1*9的，读入的时候对非0的位置、用过的数字进行标记。然后从第1个空开始填，填完之后去检查是否每行、每列、对角线的三个数之和是15。是的话就记录下来，计数器自增。剪枝：当计算器大于1时就不用再找了。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 int a[11], cnt;
 5 bool vis[11], book[11];
 6 int flag, b[11][11];
 7 
 8 void check() {
 9     int t[11];
10     for(int i=1; i<=10; ++i) t[i] = 0;
11     for(int j=0,i=1; i<=3; ++i,j+=2) {
12         t[1] += a[i];    // 123 第一行 
13         t[2] += a[i+3];    // 456 第二行 
14         t[3] += a[i+6];    // 789 第三行 
15         t[4] += a[i+j];    // 147 第一列 
16         t[5] += a[i+j+1];// 258 第二列 
17         t[6] += a[i+j+2];// 369 第三列 
18         t[7] += a[2*i+j-1];// 159
19         t[8] += a[j+3];    // 357
20     }
21     for(int i=1; i<=8; ++i) {
22         if(t[i] != 15)
23             return ;
24     }
25     // 满足 复制到b里面 
26     flag ++;
27     for(int i=1; i<=9; ++i)
28         b[flag][i] = a[i];
29     return ;
30 }
31 
32 void dfs(int x) { // 第x个空 
33     if(flag > 1) return ;// 剪枝 有多个解了 
34     if(x > 9) {
35         check();
36         return ;
37     }
38     if(vis[x]) { // 该空有数字 
39         dfs(x+1);
40         return ;
41     }
42     for(int i=1; i<=9; ++i) {
43         if(!book[i]) {
44             a[x] = i;
45             book[i] = true;
46             dfs(x+1);
47             book[i] = false;
48         }
49     }
50 }
51 
52 void Print() {  
53     for(int i=1; i<=9; ++i) {
54         printf("%d ", b[1][i]);
55         if(!(i%3)) puts("");
56     }
57     
58 }
59 
60 int main() {
61     memset(vis, false, sizeof(vis));
62     memset(book, false, sizeof(book));
63     for(int i=1; i<=9; ++i) {
64         scanf("%d", &a[i]);
65         if(a[i]) {
66             vis[i] = true;// 非0的地方不用搜索 
67             book[a[i]] = true;
68         }
69     }
70     dfs(1);
71     if(flag == 1) Print(); // 一组解就打印 
72     else printf("Too Many");
73     return 0;
74 }

9.九宫幻方

9.拉马车

小的时候，你玩过纸牌游戏吗？
有一种叫做“拉马车”的游戏，规则很简单，却很吸引小朋友。

其规则简述如下：
假设参加游戏的小朋友是A和B，游戏开始的时候，他们得到的随机的纸牌序列如下：
A方：[K, 8, X, K, A, 2, A, 9, 5, A]
B方：[2, 7, K, 5, J, 5, Q, 6, K, 4]

其中的X表示“10”，我们忽略了纸牌的花色。

从A方开始，A、B双方轮流出牌。

当轮到某一方出牌时，他从自己的纸牌队列的头部拿走一张，放到桌上，并且压在最上面一张纸牌上（如果有的话）。

此例中，游戏过程：
A出K，B出2，A出8，B出7，A出X，此时桌上的序列为：

K,2,8,7,X

当轮到B出牌时，他的牌K与桌上的纸牌序列中的K相同，则把包括K在内的以及两个K之间的纸牌都赢回来，放入自己牌的队尾。注意：为了操作方便，放入牌的顺序是与桌上的顺序相反的。
此时，A、B双方的手里牌为：
A方：[K, A, 2, A, 9, 5, A]
B方：[5, J, 5, Q, 6, K, 4, K, X, 7, 8, 2, K]

赢牌的一方继续出牌。也就是B接着出5，A出K，B出J，A出A，B出5，又赢牌了。
5,K,J,A,5
此时双方手里牌：
A方：[2, A, 9, 5, A]
B方：[Q, 6, K, 4, K, X, 7, 8, 2, K, 5, A, J, K, 5]

注意：更多的时候赢牌的一方并不能把桌上的牌都赢走，而是拿走相同牌点及其中间的部分。但无论如何，都是赢牌的一方继续出牌，有的时候刚一出牌又赢了，也是允许的。

当某一方出掉手里最后一张牌，但无法从桌面上赢取牌时，游戏立即结束。

对于本例的初始手牌情况下，最后A会输掉，而B最后的手里牌为：

9K2A62KAX58K57KJ5

本题的任务就是已知双方初始牌序，计算游戏结束时，赢的一方手里的牌序。当游戏无法结束时，输出-1。

输入为2行，2个串，分别表示A、B双方初始手里的牌序列。
输出为1行，1个串，表示A先出牌，最后赢的一方手里的牌序。

例如，
输入：
96J5A898QA
6278A7Q973

则程序应该输出：
2J9A7QA6Q6889977

再比如，
输入：
25663K6X7448
J88A5KJXX45A

则程序应该输出：
6KAJ458KXAX885XJ645

我们约定，输入的串的长度不超过30

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

提交程序时，注意选择所期望的语言类型和编译器类型。

----------------------------

笨笨有话说：
不断删除前边的，又要后边添加.... 如果用数组，需要开一个大点的，请佛祖保佑在游戏结束前，不会用到数组的边缘。

歪歪有话说：
反正串也不长，不如每次操作都返回一个新的串。

默默有话说：
我一般都不吱声，这是典型的队列结构，动态数组最好，没有？自己造一个呗！

思路：一道模拟题，就按照规则来一步一步实现。用STL中的queue会简单一点，但本人太菜，用的数组。

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 
 4 bool draw;
 5 int cnt, Win;
 6 int A_s, A_e, B_s, B_e, len, who; 
 7 char A[20001], B[20001], Z[20001];
 8 
 9 void init() { // 读入 初始化 
10     cin >> A;
11     A_s = 0, A_e = strlen(A)-1;
12     cin >> B;
13     B_s = 0, B_e = strlen(B)-1;
14     len = 0, who = 1, draw = false;
15     cnt = 0, Win = 0;
16 }
17 
18 void print() { // 输出胜者手里的牌 
19     if(Win == 1) 
20         for(int i=A_s; i<=A_e; ++i)
21             printf("%c", A[i]);
22     if(Win == 2) 
23         for(int i=B_s; i<=B_e; ++i)
24             printf("%c", B[i]);
25 }
26 
27 bool check(char ch) { // 检测出的牌桌面上有没有 
28     for(int i=len; i>0; --i)
29         if(Z[i] == ch) return true;
30     return false;
31 }
32 
33 void work_A() { // A出牌 
34     if(check(A[A_s])) { // 桌上有，开始退牌 
35         char t = A[A_s++];
36         A[++A_e] = t;
37         while(Z[len] != t) A[++A_e] = Z[len--];
38         A[++A_e] = Z[len--];
39         who = -1;
40     }
41     else Z[++len] = A[A_s++]; // 没有 放上去 
42     if(A_s > A_e) // 手里没牌了 B赢了 
43         Win = 2;
44     return ;
45 }
46 
47 void work_B() { // 同上 
48     if(check(B[B_s])) {
49         char t = B[B_s++];
50         B[++B_e] = t;
51         while(Z[len] != t) B[++B_e] = Z[len--];
52         B[++B_e] = Z[len--];
53         who = -2;
54     }
55     else Z[++len] = B[B_s++];
56     if(B_s > B_e) 
57         Win = 1;
58     return ;
59 }
60 
61 void solve() {
62     if(who == 1) work_A();
63     else if(who == 2) work_B();
64     return ;
65 }
66 
67 int main() {
68     init();
69     while(!draw && !Win) {
70         solve();
71         if(cnt++ > 1000) draw = true; // 来来回回1q次，判定为平局 
72         if(who == 1) who = 2; // 当前是A出的牌 下次为B 
73         else if(who == 2) who = 1; // 当前是B出的牌 下次为A 
74         else if(who == -1) who = 1; // A赢牌了 还是A 
75         else if(who == -2) who = 2; // B赢牌了 还是B 
76     }
77     if(draw) cout << -1 << endl; // 平局 
78     else print(); // 非平局 输出 
79     return 0;
80 }

9.拉马车

10.图形排版

小明需要在一篇文档中加入 N 张图片，其中第 i 张图片的宽度是 Wi，高度是 Hi。
假设纸张的宽度是 M，小明使用的文档编辑工具会用以下方式对图片进行自动排版：

1. 该工具会按照图片顺序，在宽度 M 以内，将尽可能多的图片排在一行。该行的高度是行内最高的图片的高度。例如在 M=10 的纸张上依次打印 3x4, 2x2, 3x3 三张图片，则效果如下图所示，这一行高度为4。(分割线以上为列标尺，分割线以下为排版区域；数字组成的矩形为第x张图片占用的版面)

2. 如果当前行剩余宽度大于0，并且小于下一张图片，则下一张图片会按比例缩放到宽度为当前行剩余宽度(高度向上取整)，然后放入当前行。例如再放入一张4x9的图片，由于剩余宽度是2，这张图片会被压缩到2x5，再被放入第一行的末尾。此时该行高度为5：

3. 如果当前行剩余宽度为0，该工具会从下一行开始继续对剩余的图片进行排版，直到所有图片都处理完毕。此时所有行的总高度和就是这 N 张图片的排版高度。例如再放入11x1, 5x5, 3x4 的图片后，效果如下图所示，总高度为11：

现在由于排版高度过高，图片的先后顺序也不能改变，小明只好从 N 张图片中选择一张删除掉以降低总高度。他希望剩余N-1张图片按原顺序的排版高度最低，你能求出最低高度是多少么？

输入：
第一行包含两个整数 M 和 N，分别表示纸张宽度和图片的数量。
接下来 N 行，每行2个整数Wi, Hi，表示第 i 个图大小为 Wi*Hi。

对于30%的数据，满足1<=N<=1000
对于100%的数据，满足1<=N<=100000，1<=M, Wi, Hi<=100

输出：
一个整数，表示在删除掉某一张图片之后，排版高度最少能是多少。

样例输入：
4 3
2 2
2 3
2 2

样例输出：
2

另一个示例，
样例输入：
2 10
4 4
4 3
1 3
4 5
2 1
2 3
5 4
5 3
1 5
2 4

样例输出：
17

资源约定：
峰值内存消耗（含虚拟机） < 256M
CPU消耗 < 2000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

提交程序时，注意选择所期望的语言类型和编译器类型。

未完全理解，请参考：https://blog.csdn.net/weixin_40367307/article/details/88554037

posted on 2020-03-16 17:16 Marginalin 阅读(2233) 评论(0) 编辑收藏举报

刷新页面返回顶部

Marginalin