2015-第六届蓝桥杯大赛个人赛省赛(软件类)真题 C大学A组
题目一览:
1.方程整数解
2.星系炸弹
3.奇妙的数字
4.格子中输出
5.九数组分数
6.牌型种数
7.手链样式
8.饮料换购
9.垒骰子
10.灾后重建
1.方程整数解
方程: a^2 + b^2 + c^2 = 1000
这个方程有整数解吗?有:a,b,c=6,8,30 就是一组解。
你能算出另一组合适的解吗?
请填写该解中最小的数字。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
思路:直接暴力枚举即可。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int main() { 5 for(int i=1; i<=32; ++i) { 6 for(int j=i; j<=32; ++j) { 7 if((i*i+j*j) > 1000) continue; 8 for(int k=j; k<=32; ++k) { 9 if((i*i+j*j+k*k) == 1000) { 10 printf("%d %d %d\n", i, j, k); 11 } 12 } 13 } 14 } 15 return 0; 16 }
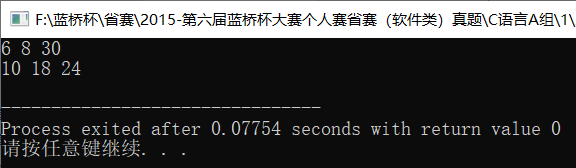
答案:10
2.星系炸弹
在X星系的广袤空间中漂浮着许多X星人造“炸弹”,用来作为宇宙中的路标。
每个炸弹都可以设定多少天之后爆炸。
比如:阿尔法炸弹2015年1月1日放置,定时为15天,则它在2015年1月16日爆炸。
有一个贝塔炸弹,2014年11月9日放置,定时为1000天,请你计算它爆炸的准确日期。
请填写该日期,格式为 yyyy-mm-dd 即4位年份2位月份2位日期。比如:2015-02-19
请严格按照格式书写。不能出现其它文字或符号。
思路:手算、计算器、excel都行。这里我们用大模拟。。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int days[13] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; 5 6 bool check(int y) { 7 if(y%400 == 0) return true; 8 if(y%4==0 && y%100!=0) return true; 9 return false; 10 } 11 12 int main() { 13 bool is_run = false; 14 int y = 2014, m = 11, d = 9, n = 1000; 15 for(int i=1; i<=n; ++i) { 16 d++; 17 if(m == 2) { 18 if(is_run) { 19 if(d >= 29) m++, d=0; 20 } 21 else { 22 if(d >= 28) m++, d=0; 23 } 24 } 25 else if(d>=days[m-1]) m++, d=0; 26 if(m > 12) { 27 y++, m=1; 28 is_run = check(y); 29 } 30 } 31 printf("%d-%02d-%02d\n", y, m, d); 32 return 0; 33 }
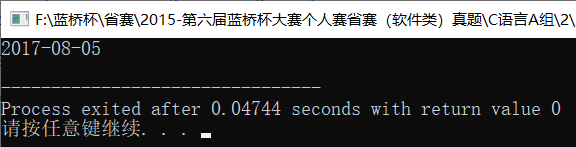
3.奇妙的数字
小明发现了一个奇妙的数字。它的平方和立方正好把0~9的10个数字每个用且只用了一次。
你能猜出这个数字是多少吗?
请填写该数字,不要填写任何多余的内容。
思路:直接暴力枚举+判断

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int cnt[11]; 5 6 void calc(int x) { 7 while(x) { 8 cnt[x%10]++; 9 x /= 10; 10 } 11 } 12 13 bool check(int x) { 14 int xx = x * x, xxx = x * x * x, len = 0; 15 for(int i=0; i<10; ++i) cnt[i] = 0; 16 bool flag = true; 17 calc(xx); calc(xxx); 18 for(int i=0; i<10; ++i) 19 if(cnt[i] == 0) flag = false; 20 return flag; 21 } 22 23 int main() { 24 int n = 9; 25 while(true) { 26 n++; 27 bool is_ok = check(n); 28 if(is_ok) break; 29 } 30 printf("%d\n", n); 31 return 0; 32 }

4.格子中输出
StringInGrid函数会在一个指定大小的格子中打印指定的字符串。
要求字符串在水平、垂直两个方向上都居中。
如果字符串太长,就截断。
如果不能恰好居中,可以稍稍偏左或者偏上一点。
下面的程序实现这个逻辑,请填写划线部分缺少的代码。
1 #include <stdio.h> 2 #include <string.h>
3 void StringInGrid(int width, int height, const char* s) { 4 int i,k; 5 char buf[1000]; 6 strcpy(buf, s); 7 if(strlen(s)>width-2) buf[width-2]=0; 8 9 printf("+"); 10 for(i=0;i<width-2;i++) printf("-"); 11 printf("+\n"); 12 13 for(k=1; k<(height-1)/2;k++){ 14 printf("|"); 15 for(i=0;i<width-2;i++) printf(" "); 16 printf("|\n"); 17 } 18 19 printf("|"); 20 21 printf("%*s%s%*s",____________); //填空 22 23 printf("|\n"); 24 25 for(k=(height-1)/2+1; k<height-1; k++){ 26 printf("|"); 27 for(i=0;i<width-2;i++) printf(" "); 28 printf("|\n"); 29 } 30 31 printf("+"); 32 for(i=0;i<width-2;i++) printf("-"); 33 printf("+\n"); 34 } 35 36 int main() { 37 StringInGrid(20,6,"abcd1234"); 38 return 0; 39 }
对于题目中数据,应该输出:
+------------------+
| |
| abcd1234 |
| |
| |
+------------------+
(如果出现对齐问题,参看【图1.jpg】)

注意:只填写缺少的内容,不要书写任何题面已有代码或说明性文字。
思路:这里先介绍一下*修饰符。在scanf里面,*是起到过滤读入的作用,比如说有3个数,而你只想读入第2个数,那么可以写scanf("%*d%d%*d", &a)来实现如下图
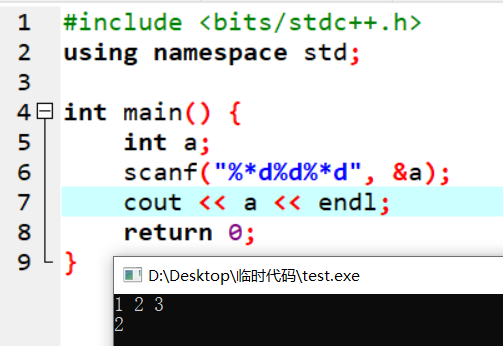
但是*到了printf里面就不一样了,printf("%3d", a);大家应该都知道这是设置宽域的,同理,%3s也是宽域。假设我们需要动态的设置宽域怎么办呢。这时候就需要*修饰符了,printf("%*s", 3,"ab");大伙应该有点想法了吧。就是把"ab"放入宽域为3的空间中右对齐。那么这道题就很简单了。
答案:
(width-2-strlen(buf))/2,"", buf, (width-1-strlen(buf))/2,""
5.九数组分数
1,2,3...9 这九个数字组成一个分数,其值恰好为1/3,如何组法?
下面的程序实现了该功能,请填写划线部分缺失的代码。
1 #include <stdio.h> 2 3 void test(int x[]) { 4 int a = x[0]*1000 + x[1]*100 + x[2]*10 + x[3]; 5 int b = x[4]*10000 + x[5]*1000 + x[6]*100 + x[7]*10 + x[8]; 6 7 if(a*3 == b) printf("%d / %d\n", a, b); 8 } 9 10 void f(int x[], int k) { 11 int i,t; 12 if(k>=9){ 13 test(x); 14 return; 15 } 16 17 for(i=k; i<9; i++) { 18 {t=x[k]; x[k]=x[i]; x[i]=t;} 19 f(x,k+1); 20 ___________________// 填空处 21 } 22 } 23 24 int main() { 25 int x[] = {1,2,3,4,5,6,7,8,9}; 26 f(x,0); 27 return 0; 28 }
注意:只填写缺少的内容,不要书写任何题面已有代码或说明性文字。
思路:很显然写的是一个dfs,所以很容易联想到回溯,然后答案就出来了。
答案:
{t=x[k]; x[k]=x[i]; x[i]=t;}
6.牌型种数
小明被劫持到X赌城,被迫与其他3人玩牌。
一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。
这时,小明脑子里突然冒出一个问题:
如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序,自己手里能拿到的初始牌型组合一共有多少种呢?
请填写该整数,不要填写任何多余的内容或说明文字。
方法一:由于是直接提交答案,没有时间限制,我们可以暴力枚举每一张牌拿的张数,最后判断手里是不是13张。我的电脑运行时间在4.6s左右。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int a[14], ans; 5 6 int main() { 7 for(a[1]=0; a[1]<=4; ++a[1]) 8 for(a[2]=0; a[2]<=4; ++a[2]) 9 for(a[3]=0; a[3]<=4; ++a[3]) 10 for(a[4]=0; a[4]<=4; ++a[4]) 11 for(a[5]=0; a[5]<=4; ++a[5]) 12 for(a[6]=0; a[6]<=4; ++a[6]) 13 for(a[7]=0; a[7]<=4; ++a[7]) 14 for(a[8]=0; a[8]<=4; ++a[8]) 15 for(a[9]=0; a[9]<=4; ++a[9]) 16 for(a[10]=0; a[10]<=4; ++a[10]) 17 for(a[11]=0; a[11]<=4; ++a[11]) 18 for(a[12]=0; a[12]<=4; ++a[12]) 19 for(a[13]=0; a[13]<=4; ++a[13]) { 20 int t = a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]+a[9]+a[10]+a[11]+a[12]+a[13]; 21 if(t == 13) ans ++; 22 } 23 printf("%d\n", ans); 24 return 0; 25 }
方法二:此时我们可以考虑dfs,发到第i种时,手里有j张,然后搜索+[0,4]的情况,即当前牌拿0-4张。第8行的剪枝很重要,不这样剪枝就要12s左右,这样剪枝需要0.2s左右

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int cnt; 5 6 void dfs(int i, int j) { // 发到第 i种牌 手里有 j张 7 if(i > 13) return; 8 if(j > 13) return; // 剪枝 当手里的牌数大于13张时,肯定不符合。 9 if(j == 13) { 10 cnt ++; 11 return ; 12 } 13 dfs(i+1, j); 14 dfs(i+1, j+1); 15 dfs(i+1, j+2); 16 dfs(i+1, j+3); 17 dfs(i+1, j+4); 18 } 19 20 int main() { 21 dfs(0, 0); 22 printf("%d\n", cnt); 23 return 0; 24 }
方法三:我们考虑DP。f[i][j]表示拿到第i种牌时,我们手里面有j张牌 的总数。那么我们的目标是不是就是f[13][13],即拿到第13种牌时,我们手里有13张牌。那么边界就是f[1][0-4] = 1;即我们只拿第1种时,拿0-4张都只有1种方法。转移方程为:f[i][j] = ∑jk=j-4f[i-1][k];代码如下:

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int f[14][14]; 5 6 int main() { 7 for(int i=0; i<=4; ++i) f[1][i] = 1; 8 for(int i=2; i<=13; ++i) { // 第 i种牌 9 for(int j=0; j<=13; ++j) { // 要拿 j 张 10 f[i][j] += f[i-1][j]; // 第 i种一张不拿 11 if(j-1>=0) f[i][j] += f[i-1][j-1];// 第 i种拿 1张 12 if(j-2>=0) f[i][j] += f[i-1][j-2];// 第 i种拿 2张 13 if(j-3>=0) f[i][j] += f[i-1][j-3];// 第 i种拿 3张 14 if(j-4>=0) f[i][j] += f[i-1][j-4];// 第 i种拿 4张 15 } 16 } 17 printf("%d\n", f[13][13]); 18 return 0; 19 }
答案:3598180
7.手链样式
小明有3颗红珊瑚,4颗白珊瑚,5颗黄玛瑙。
他想用它们串成一圈作为手链,送给女朋友。
现在小明想知道:如果考虑手链可以随意转动或翻转,一共可以有多少不同的组合样式呢?
请你提交该整数。不要填写任何多余的内容或说明性的文字。
思路:一道排列组合题。假设12颗的颜色互不相同,那么一共有12!种排列顺序,又因现在是3颗红珊瑚,4颗白珊瑚,5颗黄玛瑙。所以我们要除去(3!+4!+5!)。然后又因为可以转动,所以还需要除以12。现在考虑翻转,但在考虑翻转之前,对称在前面只出现了一次,所以不需要考虑翻转,所以:(12!/(3! * 4! * 5!)/12)+30,翻转后为:((12!/(3! * 4! * 5!)/12)+30)/2;
答案:1170
8.饮料换购
乐羊羊饮料厂正在举办一次促销优惠活动。乐羊羊C型饮料,凭3个瓶盖可以再换一瓶C型饮料,并且可以一直循环下去(但不允许暂借或赊账)。
请你计算一下,如果小明不浪费瓶盖,尽量地参加活动,那么,对于他初始买入的n瓶饮料,最后他一共能喝到多少瓶饮料。
输入:一个整数n,表示开始购买的饮料数量(0<n<10000)
输出:一个整数,表示实际得到的饮料数
例如:
用户输入:
100
程序应该输出:
149
用户输入:
101
程序应该输出:
151
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
思路:一直模拟就好

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int main() { 5 int n, x, sum; 6 cin >> n; 7 sum = n; // 一开始的n瓶都能喝到 8 do { 9 x = n%3; // 换掉剩下的瓶盖 10 n /= 3; // 换了几瓶 11 sum += n; // 喝到了新换到的 12 n += x; // 更新当前手里的瓶盖 13 }while(n>=3); 14 cout << sum << endl; 15 return 0; 16 }
9.垒骰子
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 数字不能紧贴在一起。
「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据:n <= 5
对于 60% 的数据:n <= 100
对于 100% 的数据:0 < n <= 10^9, m <= 36
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
思路:首先一个骰子的某一个面朝上时,他是有四种状态的,因为可以旋转,所以n层的话有4^n种,我们可以先把侧面当成一样的,最后再乘上去。我们考虑用动态规划来做:f[i][j]表示第i层时,顶面点数为j的的方案数,那么f[i][j]就等于第i-1层中所有不与j相斥的方案数累加。又考虑到n<=10^9,且第i层只与第i-1层有关,因此我们可以使用滚动数组。
该方法最后几个点超时

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const LL Mod = 1e9 + 7; 5 6 int n, m, pos = 0; 7 LL res, f[2][7], Ans; 8 bool vis[7][7]; 9 int oppo[7] = {0, 4, 5, 6, 1, 2, 3}; //对应面 10 11 LL ksm(LL a, LL b) { 12 LL re = 1; 13 while(b) { 14 if(b&1) re = re * a % Mod; 15 a = a * a % Mod; 16 b >>= 1; 17 } 18 return re%Mod; 19 } 20 21 int main() { 22 cin >> n >> m; 23 memset(vis, true, sizeof(vis)); 24 for(int i=1; i<=m; ++i) { 25 int x, y; 26 scanf("%d%d", &x, &y); 27 vis[x][y] = vis[y][x] = false; 28 } 29 for(int i=1; i<=6; ++i) // 边界条件 第一层每面向上为1 30 f[pos][i] = 1; 31 for(LL i=2; i<=n; ++i) { // 枚举2-n层 32 pos = 1 - pos; //滚动 0 1交替 33 for(int j=1; j<=6; ++j) { // 点数为j的向上 34 f[pos][j] = 0; // 滚动回来先清零 35 for(int k=1; k<=6; ++k) // i-1层的顶面 36 if(vis[oppo[j]][k]) // 点数j的对应面能否不相斥 37 f[pos][j] += f[1-pos][k]; 38 f[pos][j] %= Mod; 39 } 40 } 41 42 for(int i=1; i<=6; ++i) 43 Ans = (Ans+f[pos][i]) % Mod; 44 res = ksm(4, n); 45 Ans = Ans*res % Mod; 46 cout << Ans; 47 return 0; 48 }
方法二是用矩阵快速幂来做,先挖个坑。。。
10.灾后重建
Pear市一共有N(<=50000)个居民点,居民点之间有M(<=200000)条双向道路相连。这些居民点两两之间都可以通过双向道路到达。这种情况一直持续到最近,一次严重的地震毁坏了全部M条道路。
震后,Pear打算修复其中一些道路,修理第i条道路需要Pi的时间。不过,Pear并不打算让全部的点连通,而是选择一些标号特殊的点让他们连通。
Pear有Q(<=50000)次询问,每次询问,他会选择所有编号在[l,r]之间,并且 编号 mod K = C 的点,修理一些路使得它们连通。由于所有道路的修理可以同时开工,所以完成修理的时间取决于花费时间最长的一条路,即涉及到的道路中Pi的最大值。
你能帮助Pear计算出每次询问时需要花费的最少时间么?这里询问是独立的,也就是上一个询问里的修理计划并没有付诸行动。
【输入格式】
第一行三个正整数N、M、Q,含义如题面所述。
接下来M行,每行三个正整数Xi、Yi、Pi,表示一条连接Xi和Yi的双向道路,修复需要Pi的时间。可能有自环,可能有重边。1<=Pi<=1000000。
接下来Q行,每行四个正整数Li、Ri、Ki、Ci,表示这次询问的点是[Li,Ri]区间中所有编号Mod Ki=Ci的点。保证参与询问的点至少有两个。
【输出格式】
输出Q行,每行一个正整数表示对应询问的答案。
【样例输入】
7 10 4
1 3 10
2 6 9
4 1 5
3 7 4
3 6 9
1 5 8
2 7 4
3 2 10
1 7 6
7 6 9
1 7 1 0
1 7 3 1
2 5 1 0
3 7 2 1
【样例输出】
9
6
8
8
【数据范围】
对于20%的数据,N,M,Q<=30
对于40%的数据,N,M,Q<=2000
对于100%的数据,N<=50000,M<=2*10^5,Q<=50000. Pi<=10^6. Li,Ri,Ki均在[1,N]范围内,Ci在[0,对应询问的Ki)范围内。
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 5000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
posted on 2020-03-12 23:52 Marginalin 阅读(6957) 评论(2) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号