Java实现 LeetCode 576 出界的路径数（DFS || DP）

576. 出界的路径数

给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ，你可以将球移到相邻的单元格内，或者往上、下、左、右四个方向上移动使球穿过网格边界。但是，你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大，返回 结果 mod 109 + 7 的值。

示例 1：

输入: m = 2, n = 2, N = 2, i = 0, j = 0
输出: 6
解释:

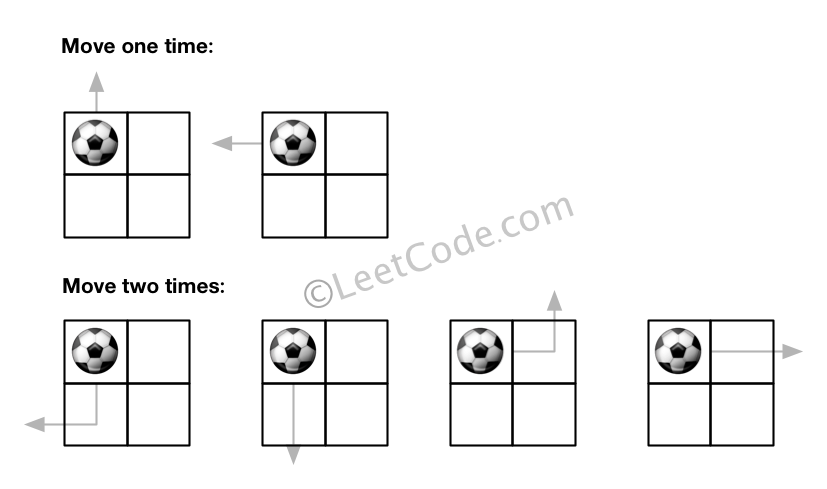
示例 2：

输入: m = 1, n = 3, N = 3, i = 0, j = 1
输出: 12
解释:

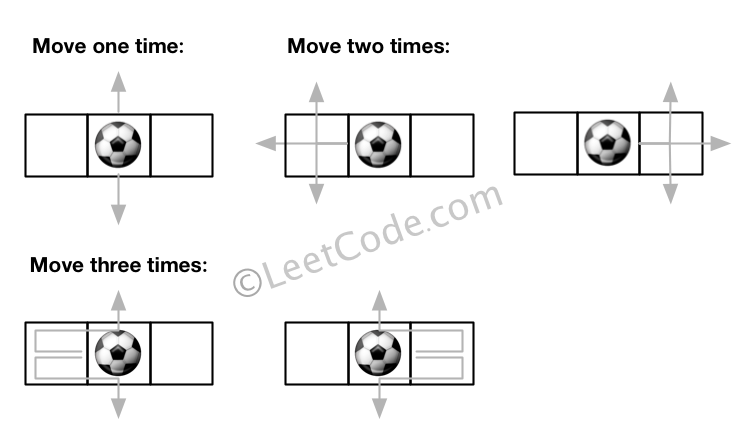
说明:

球一旦出界，就不能再被移动回网格内。
网格的长度和高度在 [1,50] 的范围内。
N 在 [0,50] 的范围内。
PS:
小编的传统的DFS
大佬弄得动态规划

class Solution {
    private Integer[][][] cache;
    
    public int findPaths(int m, int n, int N, int i, int j) {
        cache = new Integer[m][n][N+1];
        return dfs(m,n,N,j,i);
    }
    
    private int dfs(int rows,int cols,int times,int x,int y) { 
        if (isOutOfBoundary(x,y,rows,cols)) {
            return 1;
        }
        if (0 == times) {
            return 0;
        } 
        if (null != cache[y][x][times]) {
            return cache[y][x][times];
        }
        int res = (((dfs(rows,cols,times-1,x+1,y) + dfs(rows,cols,times-1,x-1,y)) % 1000000007) + ((dfs(rows,cols,times-1,x,y+1) + dfs(rows,cols,times-1,x,y-1)) % 1000000007)) % 1000000007;
        cache[y][x][times] = res;
        return res;
    }
    
    private boolean isOutOfBoundary(int x,int y,int rows,int cols) {
        return x < 0 || x >= cols || y < 0 || y >= rows;
    }
}

class Solution {
    public int findPaths(int m, int n, int N, int i, int j) {
 if(N <= 0) return 0;
        int mod = 1000000007;
        int ret = 0;
        int[][] dp = new int[m][n]; // 保存第k步的结果
        int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        
        for(int k = 1; k <= N; ++k) {
            int[][] temp = new int[m][n]; // 保存第k-1步的结果
            for(int x = 0; x < m; ++x) {
                for(int y = 0; y < n; ++y) {
                    for(int[] dir : dirs) {
                        int nx = x + dir[0];
                        int ny = y + dir[1];
                        if(nx < 0 || nx >= m || ny < 0 || ny >= n)
                            temp[x][y] += 1;
                        else
                            temp[x][y] = (dp[nx][ny] + temp[x][y]) % mod;
                    }
                }
            }
            dp = temp;
        }
        
        return dp[i][j];
    }
}