Java实现 LeetCode 743 网络延迟时间（Dijkstra经典例题）

743. 网络延迟时间

有 N 个网络节点，标记为 1 到 N。

给定一个列表 times，表示信号经过有向边的传递时间。 times[i] = (u, v, w)，其中 u 是源节点，v 是目标节点， w 是一个信号从源节点传递到目标节点的时间。

现在，我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1。

示例：

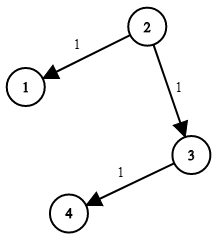
输入：times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
输出：2

注意:

N 的范围在 [1, 100] 之间。
K 的范围在 [1, N] 之间。
times 的长度在 [1, 6000] 之间。
所有的边 times[i] = (u, v, w) 都有 1 <= u, v <= N 且 0 <= w <= 100。

class Solution {
    public static int maxValue=100000;
    public int networkDelayTime(int[][] times, int N, int K) {
        //构建邻接表，用于存放各个点到各个点的距离
        int[][] matrix=new int[N+1][N+1];
        for(int i=0;i<=N;i++){
            for(int j=0;j<=N;j++){
                matrix[i][j]=maxValue;
            }
        }
        //遍历times填充邻接表
        for(int[] time:times)
             matrix[time[0]][time[1]]=time[2];
        //存放 K 到各个点的最短路径，最大的那个最短路径即为结果
        int[] distance = new int[N + 1];
        //Arrays.fill(distance, -1);
        distance[K]=0;
        //判断是否找到K到达该点最短路径
        boolean[] visited = new boolean[N + 1];
        visited[K] = true;
        for(int i=1;i<=N-1;i++){
            int min=Integer.MAX_VALUE;
            int index=-1;
            for(int j=1;j<=N;j++){
                if(!visited[j] && matrix[K][j]<min){
                    min=matrix[K][j];
                    index=j;
                }
            }
            distance[index]=min;
            visited[index]=true;
             for(int k=1;k<=N;k++){
                if(!visited[k] && matrix[K][index]+matrix[index][k]<matrix[K][k]){
                    matrix[K][k]=matrix[K][index]+matrix[index][k];
                }
            }
        }
         int maxDistance = 0;
        // 遍历最大值，如果有节点未被访问，返回 -1，否则返回最大最短路径
        for (int i = 1; i <= N; i++) {
            if (distance[i] ==maxValue) {
                return -1;
            }
            maxDistance = Math.max(distance[i], maxDistance);
        }

        return maxDistance;
    }

}