【Acwing123】士兵

【Acwing123】士兵

Description

给定 \(n\) (\(n \leq 10^4\)) 个点，每个点坐标为 \((x, y)\)。

你可以进行若干次操作，每次操作将一个点向上下左右四个方向一个一个单位。

求最少需要多少次操作，使得所有点 \(y\) 坐标相等， \(x\) 坐标相邻。

Input

第一行输入整数 \(N\)，代表点的数量。

接下来的 \(N\) 行，每行输入两个整数 \(x\) 和 \(y\) (\(|x|, |y| \leq 10^5\))，分别代表一个点的 \(x\) 坐标和 \(y\) 坐标，第 \(i\) 行即为第 \(i\) 个士兵的坐标 \(x_i, y_i\)。

Output

输出一个整数，代表所有士兵的总移动次数的最小值。

Solution

我们将 \(x\) 坐标的变化和 \(y\) 坐标的变化分开考虑。

将所有点移到同一个 \(y\) 坐标，很显然在取中位数的时候最优。

那我们直接考虑 \(x\) 坐标。

我们会发现一个最优解，它的所有点排完序后的相对位置和最终结果的相对位置是不会变化的，否则一定更劣。

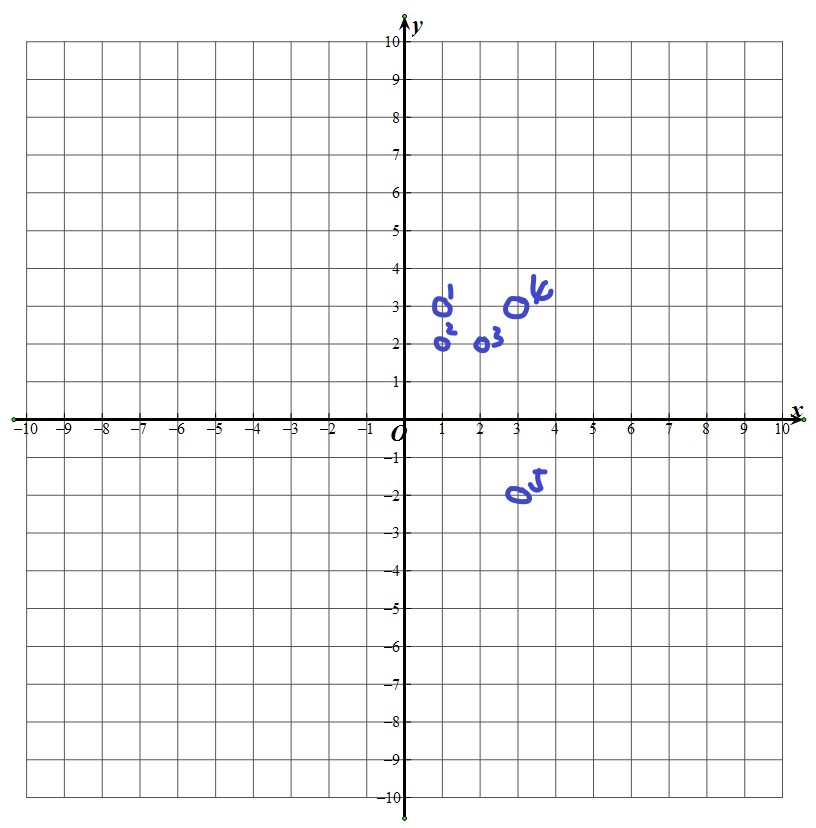
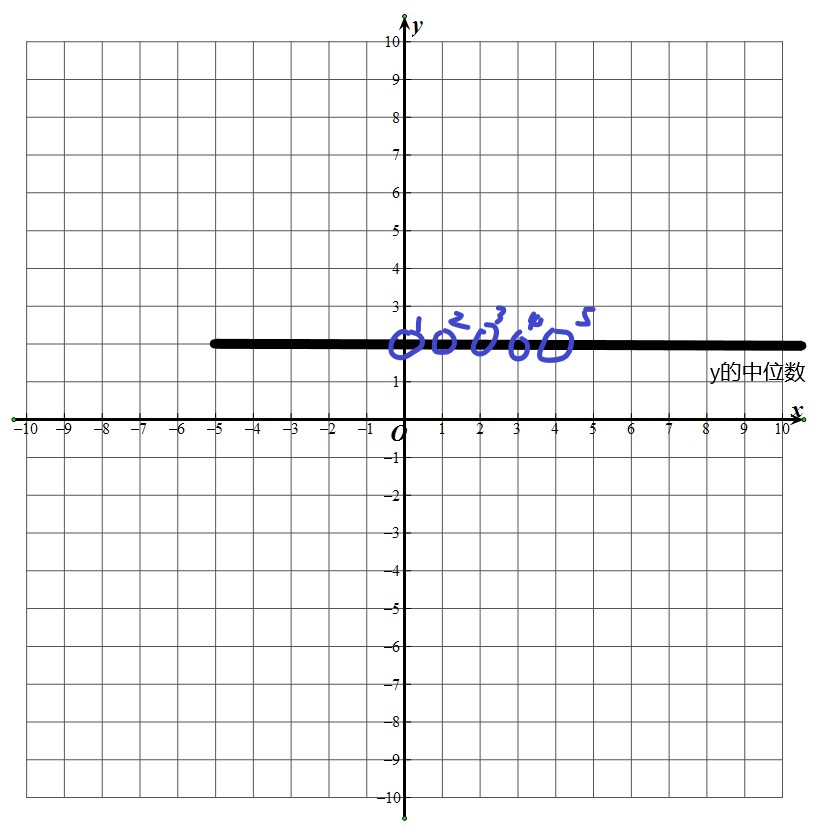
那么设按 \(x\) 坐标排完序后第一个点 \(x\)坐标为 \(a\)

那么第 \(i\) 个点的坐标即为 \(a + i - 1\)

所以对于 \(x\) 坐标变换需要的移动次数就是

\(\sum_{i = 1}^{n} |x_i - (a + i - 1)|\)

考虑重新组合一下

\(\sum_{i = 1}^{n} |(x_i - i + 1) - a|\)

那么我们令 \(z_i = x_i - i + 1\), 当 \(a\) 取到 \(z\) 的中位数时一定最优。

Submission

#include <bits/stdc++.h>

const int N = 1e4 + 5;

int n, middle, ans;
int a[N], b[N], c[N];

signed main(int argc, char *argv[]) {
    std::cin >> n;
    for (int i = 1; i <= n; ++i) std::cin >> a[i] >> b[i];
    std::sort(a + 1 ,a + 1 + n); std::sort(b + 1, b + 1 + n);

    middle = b[(n + 1) >> 1];
    for (int i = 1; i <= n; ++i) ans += std::abs(b[i] - middle);
    for (int i = 1; i <= n; ++i) c[i] = a[i] - i + 1;
    std::sort(c + 1, c + 1 + n); middle = c[(n + 1) >> 1];
    for (int i = 1; i <= n; ++i) ans += std::abs(c[i] - middle);
    return std::cout<< ans << std::endl, 0;
}