【20220225Marathon #2】联通子树

【20220225Marathon #2】联通子树

Description

给定一颗大小为 \(n(1 \leq n \leq 10^5)\) 的树。你可以指定一个1 \(\cdots n\) 的排列 \(p\), 但是得满足 \(\forall i, p_1, p_2, \cdots, p_i\) 在树上是连通的。

求满足要求的 \(p\) 的数量。

Input

第一行给定一个正整数 \(n\)，
下面 \(n - 1\) 行每行给定两个不同的正整数 \(u, v (u, v \leq n)\) 表示 \(u, v\) 有一条树边。

Output

一行一个正整数表示满足条件的 \(p\) 的数量，答案 \(mod \ 10^9 + 7\)

Solution

对于一颗树形结构，此类问题通常使用树形dp或树上启发式合并。

而此题是无根树，树上启发式合并显然不太现实。

而树形dp显然可以通过枚举根，对于每个根计算方案数解决此题。

先假设根是存在的，对于以 \(u\) 为根的子树并从 \(u\) 开始标记的方案数，我们记为 \(f_u\), 可以分以下情况讨论:

• \(size_u = 1\) 即该节点为叶子节点，那么显然 \(f_u = 1\)。
• \(size_u > 1\) 即该节点为非叶子节点，那么 \(f_u = \prod_{v \in son_u} \frac{f_v}{size_v!} \times (size_u - 1)!\)

先看下图

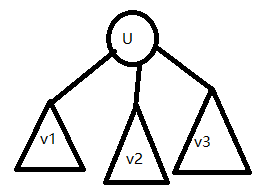
我们有两种方法推导（理性 or 感性）

• 首先考虑对于每颗子树 \(v_i\)，它的方案数有 \(f_{v_i}\)，在产生合法方案时，可以将所有 \(v_i\) 交叉排列，但是每颗 \(v_i\) 排列后的相对顺序的方案数依旧为 \(f_{v_i}\)。所以此时 \(f_u = \prod_{i = 1}^{son_u} (f_{v_i} \times \tbinom{size_u - \sum_{j=1}^{i-1}size_{v_j} - 1}{size_{v_i}})\) 将组合数展开后得到

\[f_u = \prod_{i=1}^{son_u}f_{v_i} \times \frac{(size_u - 1)!}{size_{v_1}! \times (size_u - size_{v_1} - 1)!} \times \frac{(size_u - size_{v_1} - 1)!}{size_{v2}!(size_u-size_{v_1}-size_{v_2}-1)!} \times \cdots \times \frac{(size_u - size_{v1} - size_{v2} - \cdots - size_{v_{n-1}}-1)！}{size_{v_n}!} \]

化简后得到 \(f_u = \prod_{v \in son_u} \frac{f_v}{size_v!} \times (size_u - 1)!\)

• 还是如上考虑，对于由于交叉排列造成的顺序不同，相当于将 \(u\) 子树内的点除了 \(u\) 随机排列，但由于题目要求的限制，只能先做深度浅的节点再做深度深的节点，故子树的顺序需要保证，于是得出系数为 \(\frac{(size_u-1)!}{\prod_{v \in son_u} size_v!}\)。但是对于一颗子树的相对顺序依旧有多种方案合法，所以要乘以 \(\prod_{v \in son_u} f_v\), 然后就得出了上述动态方程\(f_u = \prod_{v \in son_u} \frac{f_v}{size_v!} \times (size_u - 1)!\)。

好的，既然你已经会了有根树的做法，相信你就可以拿到TLE

因为每个节点都可以为根，所以枚举根的复杂度为 \(\Theta(n)\) 的。

一次树形dp需要扫描一整棵树，所以复杂度也是 \(\Theta(n)\) 的。

总的时间复杂度就是 \(\Theta(n^2)\) 的。

现在就考虑优化枚举根的过程。

可以简单发现，在将根从一个点转移到另一个点时，有许多 \(f_i\) 是不会变的。

所以是有许多时间浪费的，考虑从这方面入手，只去更新可能变化的 \(f_i\)， 就可以大大优化时间复杂度。

观察下图。

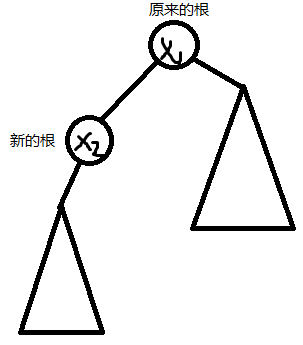
将根由 \(x_1\) 变为 \(x_2\) 时，\(x_1\)的除了\(x_2\)的其他子树(三角形那一坨)的 \(f_i\) 是不会变的。\(x_2\) 的子树也是如此。

那么就考虑更新 \(x_1\) 和 \(x_2\) 的值。

也就是由于我们只需要根节点的 \(f\) 值来更新答案，也就是 \(x_2\) 那么 \(x_1\) 就不做考虑。

可以发现，\(x_2\) 需要加上 \(x_1\) 剩下子树及 \(x_1\) 的贡献，根据上面我们推出的式子，将变化的量修改即可。

计 \(dp_i\) 为以 \(i\) 为根时的答案，得到

\[dp_y = f_y \times g_y \times \frac{1}{(size_y-1)!} \times (n-1)! \times calc(x, y) \times \frac{1}{g_y \times (n - siz[y])!} \]

其中 \(g_i = \prod_{j \in son_i} size_j!\), \(calc(x, y)\) 为根更新后原来的根的贡献。

于是我们就得到了著名的换根dp。

AC Code

#include <bits/stdc++.h>

#define int long long

const int N = 1e6 + 5, mod = 1e9 + 7;

int n, ans;
int siz[N], f[N], g[N], dp[N], fac[N], inv[N];
std::vector<int> G[N];

int qpow(int x, int y, int mod) { //快速幂
	int ans = 1;
	for (; y; y >>= 1, x = 1ll * x * x % mod)
		if (y & 1) ans = 1ll * ans * x % mod;
	return ans % mod;
}

void dfs(int x, int fa) { //这个dfs求以1为根时的f，g值
	siz[x] = f[x] = g[x] = 1;
	for (int y : G[x]) {
		if (y == fa) continue;
		dfs(y, x);
		siz[x] += siz[y];
		f[x] = 1ll * f[x] * inv[siz[y]] % mod;
		f[x] = 1ll * f[x] * f[y] % mod;
		g[x] = 1ll * g[x] * fac[siz[y]] % mod;
	} f[x] = 1ll * f[x] * fac[siz[x] - 1] % mod;
}

int ginv(int x) {return qpow(x, mod - 2, mod);} //ginv(x)为x的逆元
int calc(int x, int y) {return 1ll * ginv(f[y]) * fac[siz[y]] % mod * dp[x] % mod * ginv(fac[n - 1]) % mod * fac[n - 1 - siz[y]] % mod;}

// calc求将x为根变为y为根，x对y的贡献

void dfs2(int x, int fa) { // dfs2从1开始，以枚举根，同时累计答案
	for (auto y : G[x]) {
		if (y == fa) continue;
		dp[y] = 1ll * f[y] * g[y] % mod * inv[siz[y] - 1] % mod * fac[n - 1] % mod * calc(x, y) % mod * ginv(1ll * g[y] * fac[n - siz[y]] % mod) % mod;
		ans = (1ll * ans + dp[y]) % mod;
		dfs2(y, x);
	} return;
}

signed main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	
	std::cin >> n;
	for (int i = 1, u, v; i < n; ++i) {
		std::cin >> u >> v;
		G[u].emplace_back(v);
		G[v].emplace_back(u);
	}
	fac[0] = 1; //预处理阶乘和逆元 fac[i]表示i的阶乘， inv[i]表示fac[i]的逆元
	for (int i = 1; i <= n; ++i) fac[i] = 1ll * fac[i - 1] * i % mod;
	inv[n] = qpow(fac[n], mod - 2, mod);
	for (int i = n - 1; ~i; --i) inv[i] = 1ll * inv[i + 1] * (i + 1) % mod;
	
	dfs(1, 0);
	dp[1] = f[1]; //先将以1为根的时候的答案统计进去，因为在dfs2里不会算到
	ans = dp[1];
	dfs2(1, 0);
	return std::cout << ans << std::endl, 0;
}