[ZJOI2012]波浪

波浪

题意简述

更好的阅读体验

给出 \(n,m,k\) 三个正整数。

计算对于 \(n\) 阶排列 \(p\) 波动值小于 \(m\) 的概率。

其中对于一个排列的波动值的定义如下。

\(\sum_{i=2}^{n}|p_i-p_{i-1}|\)

\(n \leq 100, k \leq 30, m \leq 2147483647\)

题目分析

考虑计算的时候肯定要去掉绝对值。

那么就要确定二者大小关系。

于是想到了按照数值大小来插入。

那么在它前面插入的数都严格小于它。

这个时候可以单独计算这个数对整个数列的贡献。

你可以发现以下性质：

1. 每个数的贡献与当前(指插入的时候)的排列 即已插入的数有关。

2. 上条性质中的贡献只与它们的相对位置有关。

于是很容易就可以想到，可以用方案dp解决该题。

根据性质2可以联想到把连续的数当作1个联通块。

所以设计dp状态。

\(f_{i,j,k,l}\)表示当前插入第\(i\)个数，波动值为\(j\)，构成了\(k\)个联通块，其中有\(l\)个边界(1或n)已经插入了数字。

为什么要加入边界这一维呢？ 看图。

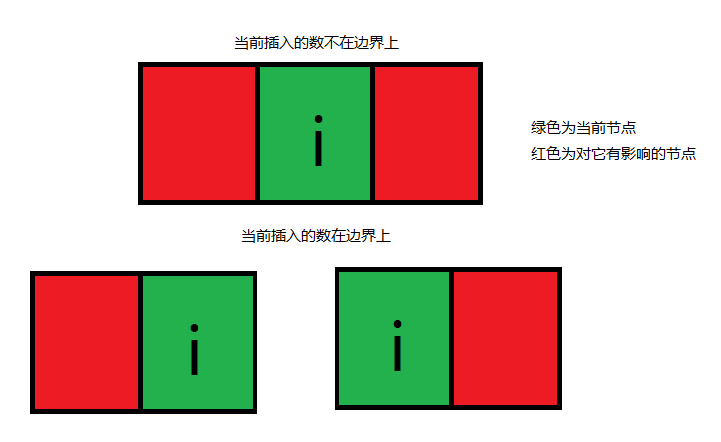
对于不在边界上的数，它对左右两边都有影响。

而边界上的数只对其中一个有影响（另一边没有数，越界了）。

那么现在就可以推dp式子了。

1. 当前结点不在边界上

   • 它的两边都没有数 那么两个数都比它大 贡献为\(-2i\) 总共有\((k - l + 1)\)个这样的数 且加入后新增一个联通块。 \(f_{i,j-2i,k+1,l} = f_{i-1,j,k,l} \times (k - l + 1) + f_{i,j-2i,k+1,l}\)

   • 它的一边有数 那么两个数一个大一个小 贡献为\(0\) 总共有\((2k-l)\)个这样的数 扩展了此联通块故数量不变。 \(f_{i,j,k,l} += f_{i-1,j,k,l} \times (2k - l)\)

   • 它的两边都有数 那么两个数都比它小 贡献为\(2i\) 总共有\((k - 1)\)个这样的数 这个操作相当于合并两个联通块所以联通块数量-1。 \(f_{i,j+2i,k-1,l} += f_{i-1,j,k,l} \times (k - 1)\)

2. 当前结点在边界上

   • 它的旁边有数 那么那个数比它小 贡献\(i\) 总共有\((2 - l)\)个这样的数 联通块扩展个数不变 新增一个边界节点。 \(f_{i,j+i,k,l+1} += f_{i-1,j,k,l} \times (2 - l)\)

   • 它的旁边有数 那么那个数比它大 贡献\(-i\) 总共有\((2 - l)\)个这样的数 新增一个联通块和一个边界节点。 \(f_{i,j-i,k+1,l+1} += f_{i-1,j,k,l} \times (2 - l)\)

注意

• 由于有负的贡献 C++里是没有负下标的 所以整体加上一个M(最大贡献) 其中因为\(n \leq 100\) 所以\(m \leq 5050\)。

• 题目中求的是不小于m 即大于等于m的 别看错了。

• 普通的方案dp再除以总方案(\(n!\))求概率会掉精度 所以在dp时转移方程都除以\(i\)。

• 算一下空间发现不够 但由于转移只要用到上一项 所以滚动一下数组 这也是常考的。

• 题目中要保留精度 当\(k \leq 8\)时可以用long double 但大于8时要用高精度浮点数或者__float128(本文所使用的是__float128因为博主菜不会写浮点高精)。

• 要手写输出Output。

总结

从现在看来这道题整体不算难。

但是很多人没使用long double、__float128(貌似是禁用的)或者高精浮点。

所以挂分率是偏高的 而且精度的问题也容易挂分。

总体来说还是细节挺多的 所以成了黑题。

Code

#include <bits/stdc++.h>

using namespace std;

const int M = 5050, N = 105;

int read(int x = 0, bool f = false, char ch = getchar()) {
	for (; !isdigit(ch); ch = getchar()) f |= (ch == '-');
	for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
	return f ? ~x + 1 : x;
}

int n, m, k;

namespace Float{
	__float128 dp[2][2 * M + 5][N][3];
};

namespace Double{
	long double dp2[2][2 * M + 5][N][3];
};

const long double eps = 1e-14;

template<class T>
void output(T ans) {
	if (ans + eps >= 1) cout << "1." << string(k, '0') << endl;
	else {
		printf("0.");
		ans *= 10;
		for (int i = 1; i <= k; ++i)
			printf("%d", (int)(ans + (i == k) * 0.5)),
			ans = (ans - (int)ans) * 10;
	}
}

template<class T>
void solve(T f[][2 * M + 5][N][3]) {
	f[0][M][0][0] = 1;
	int now = 1;
	for (int i = 1; i <= n; ++i) {
		memset(f[now], 0, sizeof f[now]);
		for (int j = 0; j <= 2 * M; ++j)
			for (int k = 0; k < i; ++k)
				for (int l = 0; l < 3; ++l) {
					if (!f[now ^ 1][j][k][l]) continue;
					if (j - 2 * i >= 0) f[now][j - 2 * i][k + 1][l] += f[now ^ 1][j][k][l] * (k - l + 1) / i;
					if (k) f[now][j][k][l] += f[now ^ 1][j][k][l] * (2 * k - l) / i;
					if (j + 2 * i <= 2 * M) f[now][j + 2 * i][k - 1][l] += f[now ^ 1][j][k][l] * (k - 1) / i;
					if (l < 2) {
						if (j + i <= 2 * M) f[now][j + i][k][l + 1] += f[now ^ 1][j][k][l] * (2 - l) / i;
						if (j - i >= 0) f[now][j - i][k + 1][l + 1] += f[now ^ 1][j][k][l] * (2 - l) / i;
					}
				}
		now ^= 1;
	}
	T ans = 0;
	for (int i = M + m; i <= 2 * M; ++i) ans += f[n & 1][i][1][2];
	output(ans);
}

int main() {
	n = read(), m = read(), k = read();
	if (k <= 8) solve(Double::dp2);
	else solve(Float::dp);
	return 0;
}