2020ICPC沈阳站C题 Mean Streets of Gadgetzan

大致题意

原题链接

翻译

\(有n个逻辑变量 请你分别对它们赋值 使其满足m个命题\)

\(命题有四种格式:\)

• 单独数字x 表示第x个逻辑变量为真

• ! + 数字x 表示第x个逻辑变量为假

• 若干个数字\(a_1, a_2, ..., a_p\)(不给出个数) -> 数字x 表示前面的a变量全为真
  的时候x必定为真

• 若干个数字\(a_1, a_2, ..., a_p\)(不给出个数) -> ! + 数字x 表示前面的a变量全为真
  的时候x必定为假

其中每个命题之间空行 即'\n'

注: 此题含有SPJ 可能有多种方案 任意输出一种

思路

明显的构造吧

考虑对于1,2类的命题 直接给变量赋值

对3,4类的命题 可以发现一个性质

即当a数组其中任意一个或多个逻辑变量值为0时 命题必定成立

为了方便构造 尽量满足 我们尽量将此类条件按上述性质处理 即让a数组有0

那么我们只需要将全部逻辑变量初值赋值为0(false)即可

在推出一个true变量后去更新其他变量 若a数组的值全部固定不为0 则后面的x的值也固定了

注意

这题的读入有些毒瘤

例如

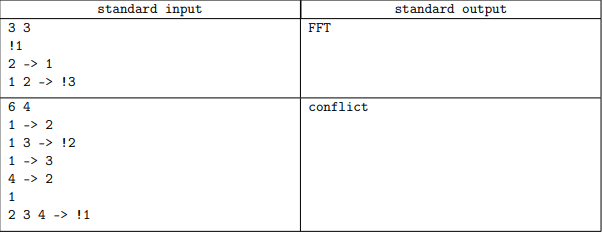
这个时候我们可以无视掉'->'因为你判断数的个数就可以推出是1,2类命题还是3,4类命题

运用快读的方法读入数字 如下:

if (isdigit(ch))
	isnum = true,
	x = (x << 1) + (x << 3) + (ch ^ 48);

当ch(读入字符)为'!'的时候 根据命题的性质 最多有一个!所以直接用bool记录一下

if(ch == '!') sign = 1;

总的读入如下

void rad(int x = 0, char ch = getchar(), bool isnum = false) {
	Num.clear(); int sign = 0;
	for (; ch != '\n' && ch != '\r' && ch != EOF; ch = getchar()) {
		if (isdigit(ch))
			isnum = true,
			x = (x << 1) + (x << 3) + (ch ^ 48);
		else {
			if (isnum) Num.push_back(x);
			x = isnum = 0; if(ch == '!') sign = 1;
		}
	}
	if (isnum) Num.push_back(x);
	if (Num.size() == 1) q.push(sign ? -Num[0] : Num[0]);
	else {
		deg[++ tot] = Num.size() - 1;
		for (auto v : Num) e[v].push_back(tot);
		to[tot] = sign? -Num[deg[tot]] : Num[deg[tot]]; 
	}
}

实现

#include <bits/stdc++.h>

using namespace std;

int read(int x = 0, bool f = false, char ch = getchar()) {
	for (; !isdigit(ch); ch = getchar()) f ^= (ch == '-');
	for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
	return f ? ~x + 1 : x;
}

const int N = 1e6 + 5;

int m, n, tot;
int dat[N], deg[N], to[N];

queue<int> q;
vector<int> Num, e[N];

void rad(int x = 0, char ch = getchar(), bool isnum = false) {
	Num.clear(); int sign = 0;
	for (; ch != '\n' && ch != '\r' && ch != EOF; ch = getchar()) {
		if (isdigit(ch))
			isnum = true,
			x = (x << 1) + (x << 3) + (ch ^ 48);
		else {
			if (isnum) Num.push_back(x);
			x = isnum = 0; if(ch == '!') sign = 1;
		}
	}
	if (isnum) Num.push_back(x);
	if (Num.size() == 1) q.push(sign ? -Num[0] : Num[0]);
	else {
		deg[++ tot] = Num.size() - 1;
		for (auto v : Num) e[v].push_back(tot);
		to[tot] = sign? -Num[deg[tot]] : Num[deg[tot]]; 
	}
}

signed main() {
	m = read(), n = read();
	for (int i = 1; i <= m; ++i) rad();
	while(q.size()) {
		int x = q.front(); q.pop();
		if (x < 0) {
			x = -x;
			if (dat[x] > 0) return puts("conflict"), 0;
			dat[x] = -1;
		} else {
			if (dat[x] < 0) return puts("conflict"), 0;
			if (dat[x]) continue; dat[x] = 1;
			for (auto v : e[x]) {
				if (!(--deg[v])) q.push(to[v]);
			}
		}
	} for (int i = 1; i <= n; ++i) putchar(dat[i] == 1? 'T' : 'F');
	return 0;
}

如果喜欢的话 点个赞再走吧