【DP优化】斜率优化
【学习笔记】斜率优化
引
在写动态规划的题的时候,时间复杂度往往太大,我们需要一些优化。
这时,斜率优化横空出世。
使用范围特别广,基本上只要是阳间一点的式子都可以。
当横坐标和斜率单调递增的时候可以用单调队列,不然就用平衡树动态维护凸包(只会口胡)。
概念
当我们在 \(i\) 这个点寻找最优决策时,会使用一个和 \(f_i\) 相关的直线,去切我们维护的凸包。切到的点即为最优决策。
该方法可以大大的减少时间复杂度,从而做到dp的优化。
我们先由例题引入。
例题
【HNOI2008】玩具装箱
题意简述
将 \(n\) 件物品分为若干段, 每一段的代价为 \((r - l + \sum_{i = l}^{r} C_i - L) ^ 2\) 其中 \(l\) 和 \(r\) 为该段的左端点和右端点, \(C_i\) 为第 \(i\) 个物品的权值, \(L\) 为给定常数。
求出一种方案,使代价之和最小,输出最小的代价。
题目分析
很明显的动态规划好题。
首先我们设计状态 \(f_i\) 表示当前到第i个物品时所用的最小代价。
显而易见最终状态为 \(f_n\)。
先不考虑时间复杂度,就可以列出状态转移方程。
显然可以用前缀和优化掉一个 \(n\),记 \(s_i\) 表示 \(C_i\) 的前缀和。
此时我们可以搞一搞事情。随便推导一下。
令 \(g_i\) 为 \(s_i + i\) ,可以做出如下变换。
假设 \(j\) 为转移点(决策点),那么就可以嘿嘿嘿。
我们发现左边在已知 \(i\) 和 \(j\) 的情况下可以 \(O(1)\) 求出,可以整体考虑。
相信机智聪明的你一定发现了这玩意特别想一次函数 \(y = kx + b\)
于是我们将它放入二维平面直角坐标系。
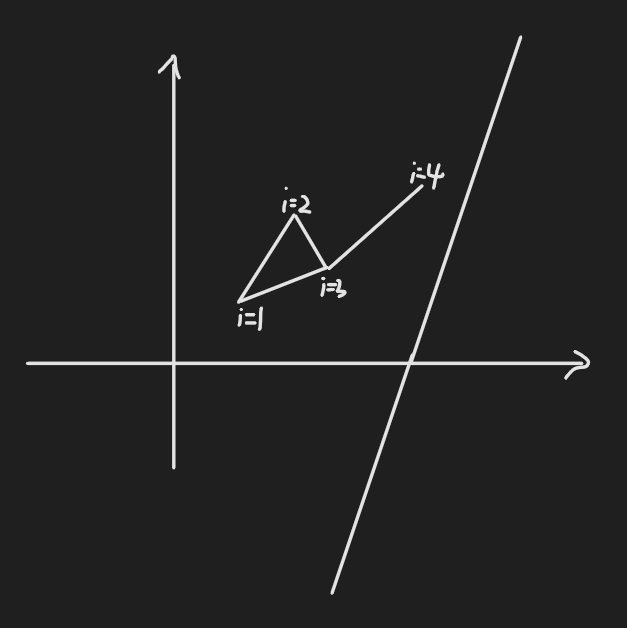
显然将 \(i_1\) 和 \(i_2\) 的截距大于 \(i_1\) 和 \(i_3\) 的截距。
而截距恰恰为 \(f_i\), 于是我们通过维护一个 \(i_1-i_3-i_4\) 的凸壳来维护答案的最大值。
(这个我会!)用类似单调队列的东西简单地维护维护。
考虑对于一个 \(f_i\) 的更新,是对前面的所有截距取一个最小值
那就搞一个队列,若第一个元素和第二个元素的斜率小于当前直线,那么就用第二个点更优,于是弹出队头,队尾更新同理。
while(head < tail && sloup(q[head], q[head + 1]) < 2 * g[i]) ++ head;
f[i] = f[q[head]] + (g[i] - g[q[head]] - L - 1) * (g[i] - g[q[head]] - L - 1);
while(head < tail && sloup(q[tail], i) < sloup(q[tail], q[tail - 1])) -- tail;
q[++ tail] = i;
注意在此道题中坐标的表示为 \((s_i, f_i + (s_i + L) ^ 2)\) 。
大家可能会问 \(s_i ^ 2\) 和 \(L\) 去哪里了。
这其实是因为在计算斜率的时候大家用的式子为 \(k = \frac{y1 - y2}{x1 - x2}\)时互相抵消掉了,可以减小常数和数值。
代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
int read(int x = 0, bool f = false, char ch = getchar()) {
for (; !isdigit(ch); ch = getchar()) f |= (ch == '-');
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return f ? ~x + 1 : x;
}
const int N = 5e4 + 5;
int n, L, head, tail;
int s[N], g[N], f[N], q[N];
double getx(int u) {return g[u];}
double gety(int u) {return f[u] + (g[u] + L) * (g[u] + L);}
double sloup(int u, int v) {return (gety(u) - gety(v)) * 1. / (getx(u) - getx(v));}
signed main() {
n = read(), L = read();
for (int i = 1; i <= n; ++i) s[i] = s[i - 1] + read();
for (int i = 1; i <= n; ++i) g[i] = s[i] + i; q[tail] = 0;
for (int i = 1; i <= n; ++i) {
while(head < tail && sloup(q[head], q[head + 1]) < 2 * g[i]) ++ head;
f[i] = f[q[head]] + (g[i] - g[q[head]] - L - 1) * (g[i] - g[q[head]] - L - 1);
while(head < tail && sloup(q[tail], i) < sloup(q[tail], q[tail - 1])) -- tail;
q[++ tail] = i;
} return printf("%lld\n", f[n]), 0;
}
分析
上述过程中,有很大的局限性。
因为 \(s_i\) 递增,所以横坐标递增,就很棒。
当弹出队头的时候,斜率小于 \(2 \times s_i\) ,后面的肯定也小于 \(2 \times s_i\) 。
如果横坐标不是递增呢?
那就用数据结构,如平衡树。(我不会啊)
任务安排(三合一)
题意简述
有 \(N\) 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这 \(N\) 个任务分成若干批,每一批包含连续的若干个任务。
从时刻 \(0\) 开始,任务被分批加工,执行第 \(i\) 个任务所需的时间是 \(T_i\) 。
另外,在每批任务开始前,机器需要 \(S\) 的启动时间,故执行一批任务所需的时间是启动时间 \(S\) 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 \(C_i\)。
请为机器规划一个分组方案,使得总费用最小。
题目分析
先看 \(n \leq 5 \cdot 10 ^ 3\) 的解法。
很容易想到 \(O(n ^ 3)\) 的式子。
令 \(C_i\) 为费用系数的前缀和, \(T_i\) 为时间的前缀和。
考虑提前费用计算,就可以优化为如下式子。
代码如下:
for (int i = 1; i <= n; ++i) {
T[i] = T[i - 1] + read();
cost[i] = cost[i - 1] + read();
} f[0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
f[i] = min(f[j] + T[i] * (cost[i] - cost[j]) + s * (cost[n] - cost[j]), f[i]);
}
} return printf("%d\n", f[n]), 0;
现在把 \(n \leq 3 \cdot 10 ^ 5\) ,需要加上斜率优化。
考虑 \(j\) 为最有决策点,可以写成下面的式子。
然后就是熟悉的一次函数,令 \(f_j = y\) , \(C_j = x\) , \(- T_i \times C_i - s \times C_n = b\)
观察到函数的凸包性质以及横坐标单调递增(因为是前缀和),于是就可以像上题一样用一个队列维护了,此时的转移方程应是:
再看任务安排三。
由于斜率并不单调了,但是横坐标依旧单调,所以就不用写平衡树了(其实是我不会)。
具体就是二分出一个斜率第一个大于等于当前斜率的点即为最优决策。
记得踢掉不在凸包上的点。
下面是代码:
for (int i = 1; i <= n; ++i) {
int l = head, r = tail;
while(l < r) {
int mid = l + r >> 1;
if ((double)f[q[mid + 1]] - f[q[mid]] > (double)(T[i] + s) * (cost[q[mid + 1]] - cost[q[mid]])) r = mid;
else l = mid + 1;
}
int pos = q[r];
f[i] = f[pos] - (T[i] + s) * cost[pos] + T[i] * cost[i] + cost[n] * s;
while(head < tail && (double)(f[q[tail]] - f[q[tail - 1]]) * (cost[i] - cost[q[tail - 1]]) >= (double)(f[i] - f[q[tail - 1]]) * (cost[q[tail]] - cost[q[tail - 1]])) -- tail;
q[++ tail] = i;
}
代码
--------------------------------
任务安排一
#include <bits/stdc++.h>
using namespace std;
#define int long long
int read(int x = 0, bool f = false, char ch = getchar()) {
for (; !isdigit(ch); ch = getchar()) f |= (ch == '-');
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return f ? ~x + 1 : x;
}
const int N = 5e3 + 5;
int n, s;
int f[N], g[N], T[N], cost[N];
signed main() {
n = read(), s = read(); memset(f, 0x3f, sizeof f);
for (int i = 1; i <= n; ++i) {
T[i] = T[i - 1] + read();
cost[i] = cost[i - 1] + read();
} f[0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
f[i] = min(f[j] + T[i] * (cost[i] - cost[j]) + s * (cost[n] - cost[j]), f[i]);
}
} return printf("%lld\n", f[n]), 0;
}
--------------------------------
任务安排二
#include <bits/stdc++.h>
using namespace std;
#define int long long
int read(int x = 0, bool f = false, char ch = getchar()) {
for (; !isdigit(ch); ch = getchar()) f |= (ch == '-');
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return f ? ~x + 1 : x;
}
const int N = 3e5 + 5;
int n, s, tail, head;
int f[N], g[N], T[N], cost[N], q[N];
double getx(int id) {return cost[id];}
double gety(int id) {return f[id];}
double sloup(int a, int b) {return (gety(a) - gety(b)) * 1. / (getx(a) - getx(b));}
signed main() {
n = read(), s = read(); memset(f, 0x3f, sizeof f);
for (int i = 1; i <= n; ++i) {
T[i] = T[i - 1] + read();
cost[i] = cost[i - 1] + read();
} f[0] = 0; q[head] = 0;
for (int i = 1; i <= n; ++i) {
while(head < tail && sloup(q[head], q[head + 1]) < T[i] + s) ++ head;
f[i] = f[q[head]] - (T[i] + s) * cost[q[head]] + T[i] * cost[i] + cost[n] * s;
while(head < tail && sloup(q[tail], i) <= sloup(q[tail], q[tail - 1])) -- tail;
q[++ tail] = i;
} return printf("%lld\n", f[n]), 0;
}
--------------------------------
任务安排三
#include <bits/stdc++.h>
using namespace std;
#define int long long
int read(int x = 0, bool f = false, char ch = getchar()) {
for (; !isdigit(ch); ch = getchar()) f |= (ch == '-');
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return f ? ~x + 1 : x;
}
const int N = 3e5 + 5;
int n, s, tail, head;
int f[N], g[N], T[N], cost[N], q[N];
signed main() {
n = read(), s = read();
for (int i = 1; i <= n; ++i) {
T[i] = T[i - 1] + read();
cost[i] = cost[i - 1] + read();
} f[0] = 0; q[head] = 0;
for (int i = 1; i <= n; ++i) {
int l = head, r = tail;
while(l < r) {
int mid = l + r >> 1;
if ((double)f[q[mid + 1]] - f[q[mid]] > (double)(T[i] + s) * (cost[q[mid + 1]] - cost[q[mid]])) r = mid;
else l = mid + 1;
}
int pos = q[r];
f[i] = f[pos] - (T[i] + s) * cost[pos] + T[i] * cost[i] + cost[n] * s;
while(head < tail && (double)(f[q[tail]] - f[q[tail - 1]]) * (cost[i] - cost[q[tail - 1]]) >= (double)(f[i] - f[q[tail - 1]]) * (cost[q[tail]] - cost[q[tail - 1]])) -- tail;
q[++ tail] = i;
} return printf("%lld\n", f[n]), 0;
}
本文来自博客园,作者:xxcxu,转载请注明原文链接:https://www.cnblogs.com/Maraschino/articles/15248533.html

 【学习笔记】斜率优化
【学习笔记】斜率优化

