随机化算法

随机化算法指，对于特定输入，该算法的输出不是固定值，而是服从某一分布。

单纯形（simplex）：一个\(k\)维单纯形是指包含\(k+1\)个顶点的凸多面体，一维单纯形是一条线段，二维单纯形是一个三角形，三维单纯形是一个四面体，以此类推推广到任意维。“单纯”意味着基本，是组成更复杂结构的基本构件。

概率单纯形（probability simplex）：是一个数学空间，上面每个点代表有限个互斥事件之间的概率分布。该空间的每条坐标轴代表一个互斥事件，\(k-1\)维单纯形上的每个点在\(k\)维空间中的坐标就是其\(k\)个互斥事件上的概率分布。每一点的坐标（向量）包含\(k\)个元素，各元素非负且和为1。

如下图所示，三个事件发生的概率分布形成一个二维的概率单纯形，上面每个点在三个事件上发生的概率之和为1。

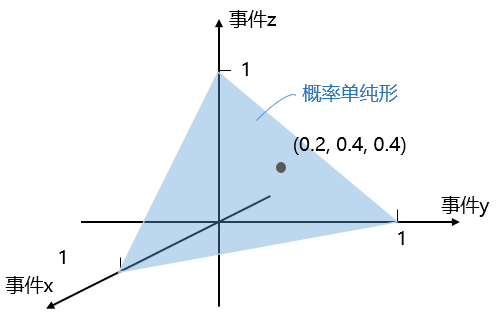
形式化定义：给定一个离散集\(B\)，\(B\)上的概率单纯形\(\Delta(B)\)被定义为

\[\Delta(B)=\left\{x \in \mathbb{R}^{|B|}\left|x_{i} \geq 0, i=1,2, \cdots,\right| B \mid ; \sum_{i=1}^{|B|} x_{i}=1\right\} \]

\(\Delta(B)\)是一个集合，集合中每一个元素是一个\(|B|\)维向量，该向量代表了一个离散型随机变量的概率分布。\(\Delta(B)\)代表了一个有\(|B|\)种取值的离散型随机变量的所有可能的概率分布。

随机化算法：一个随机化算法\(\cal{M}\)有定义域\(A\)、离散的值域\(B\)和一个映射\(\mathcal{M}:A\rightarrow \Delta(B)\)。一个输入\(a\in A\)，算法\(\cal{M}\)的输出\(\mathcal{M}(a)\in \Delta(B)\)。

例如，\(A=\{2,3,4\}\)，\(B=\{1,2,3,4,5\}\)，设\(\Delta(B)\)中包含三个元素，分别为\((\frac{1}{3},\frac{1}{3},\frac{1}{3},0,0)\)、\((0,\frac{1}{3},\frac{1}{3},\frac{1}{3},0)\)、\((0,0,\frac{1}{3},\frac{1}{3},\frac{1}{3})\)，即

\[\Delta(B)=\left\{ (\frac{1}{3},\frac{1}{3},\frac{1}{3},0,0), (0,\frac{1}{3},\frac{1}{3},\frac{1}{3},0), (0,0,\frac{1}{3},\frac{1}{3},\frac{1}{3}) \right\} \]

每个元素均代表算法输出的随机变量取值为1,2,3,4,5的概率分布，现可以规定映射\(\cal{M}\)为

\[\mathcal{M}(2)=\left(\frac{1}{3}, \frac{1}{3}, \frac{1}{3}, 0,0\right), \mathcal{M}(3)=\left(0, \frac{1}{3}, \frac{1}{3}, \frac{1}{3}, 0\right), \mathcal{M}(4)=\left(0,0, \frac{1}{3}, \frac{1}{3}, \frac{1}{3}\right) \]

也就是说，一个特定输入\(a\in A\)经过随机化算法\(\cal{M}\)得到的不是一个具体值\(b\in B\)，而是一个分布\(\mathcal{M}(a)\in \Delta(B)\)，又或者说，算法将以一定概率输出某一个值。

上述情况是在离散概率空间中讨论的，有时，算法将从连续分布中的采样，但最后将以适当的精度进行离散化。

参考资料：

1. 概率单纯形 https://zhuanlan.zhihu.com/p/479892005
2. 差分隐私的算法基础 第二章 第三节 形式化差分隐私 https://zhuanlan.zhihu.com/p/502656652