转自:https://blog.csdn.net/SimileciWH/article/details/84976187
1,理论模型
1.1 原理
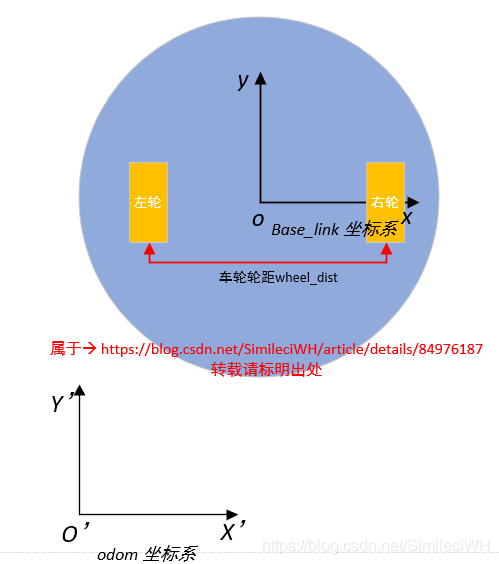
如下图所示,蓝色圆形区域为小车的地盘,左右轮之间的间距为wheel_dist,注意算法中的所有的单位,全部是国际标准单位。移动机器人编码器,安装在左右轮上,机器人地底盘的坐标系为base_link坐标系,里程计坐标系为odom。
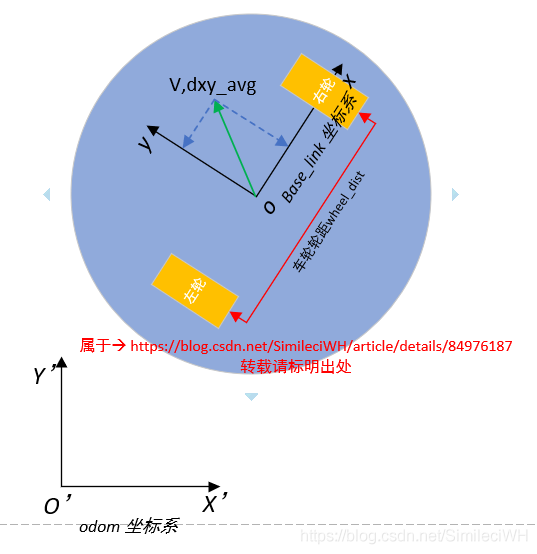
当移动机器人移动时,假设运动到如下图所示位置。图中的,V为移动小车中心点的运动速度方向,dxy_avg为移动小车中心点的运动距离。
根据编码器的差值,可知前一时刻与当前时刻编码器增量的计数脉冲,已知小车车轮行走一个周长的长度的编码器计数脉冲个数,可以推算出,一个计数脉冲的移动距离。代码实现如下:
# (4096 * 7.5) dright is right boot position dright = (right_enc - enc_right) * pi * D / (4096 * 7.5) # dleft is left boot positon dleft = (left_enc - enc_left) * pi * D / (4096 * 7.5)
其中,dright为右轮的移动距离,dleft为左轮的移动距离right_enc - enc_right为右轮编码器脉冲个数的增量,left_enc - enc_left为左轮编码器脉冲个数的增量,参数pi * D / (4096 * 7.5),需要依据自己的小车测量出,编码器一个计数脉冲对应的行走距离(单位m)。
1.2 向中心点换算
因为在使用里程计向上层的开发中,往往对于小车模型,通常会考率成中心点的运动模型,即大致认为时一个质点,这是不准确的。算法如下:
dxy_ave = (dright + dleft) / 2.0 dth = (dright - dleft) / wheel_track vxy = dxy_ave / dt vth = dth / dt
其中,dxy_ave为左右轮的移动距离均值,认为是中心点的移动距离;dth为通过为中心点的转动角度,通过弧长公式 θ = l / R \theta = l/Rθ=l/R,中心点速度V=vxy为位移对时间的微分v = d x / d t v= dx/dtv=dx/dt,vth为角速度,为转动角度对时间的倒数v t h = θ / d t vth= \theta/dtvth=θ/dt
1.3 base_link到odom坐标系的转化
在1.2节中的换算数据都是在小车底盘坐标系base_link上进行的,但是我们最终需要将这些数据转化成odom坐标系上的数据发送出去。代码如下所示:
dx = cos(dth) * dxy_ave dy = -sin(dth) * dxy_ave x += (cos(th) * dx - sin(th) * dy) y += (sin(th) * dx + cos(th) * dy)
其中,dxy_ave为中心点的在dt时间内的位移;dx&&dy分别为中心点出的位移在base_link坐标系xoy轴上的投影;然后通过两个坐标系的投影转换,即旋转矩阵求解在odom坐标系上的x’轴和y’轴的位移;前一时刻的位移加当前位移增量,即为当前位移。
可以理解成,在base_link坐标系上的x轴和y轴投影的位移,需要投影到odom坐标系上的x’轴和y’轴上,所以,d x ′ = d x ∗ c o s ( θ ) − d y ∗ s i n ( θ ) dx'=dx*cos(\theta)-dy*sin(\theta)dx
′
=dx∗cos(θ)−dy∗sin(θ),即在odom坐标系上的x’轴上的位移是由base_link坐标系上的x轴和y轴投影的位移的合成,至于为什么是“-”号,画出投影的位移分解图,就可以很清楚的看出来了。;同理可得d y ′ = d y ∗ s i n ( θ ) + d y ∗ c o s ( θ ) dy'=dy*sin(\theta)+dy*cos(\theta)dy
′
=dy∗sin(θ)+dy∗cos(θ)。
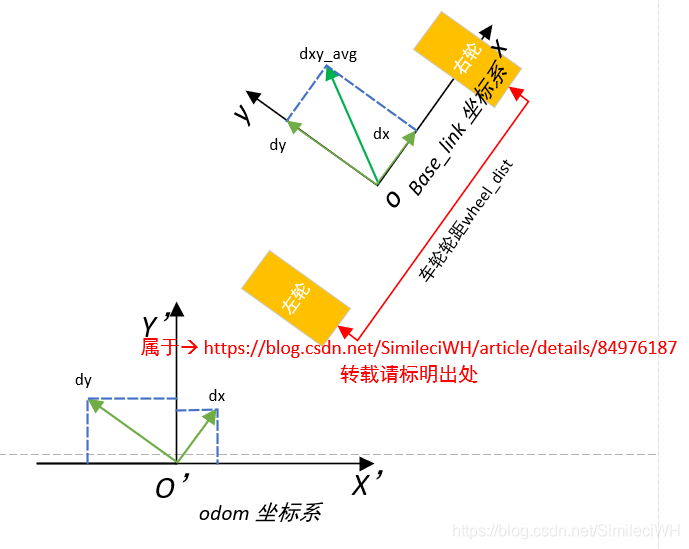
位移的分解图,如下所示
2, python源代码主要部分
下面包含了,发送odom的方式,看到这一步的大概都是理解ROS的原理了,就不细细的说明了。
now = rospy.Time.now() # record get encode left&right in first time, must initial enc_right&left get_encode_count += 1 if get_encode_count == 1: enc_right = right_enc enc_left = left_enc dt = now - then then = now dt = dt.to_sec() # Calculate odometry if enc_left is None: dright = 0 dleft = 0 else: # (4096 * 7.5) dright is right boot position dright = (right_enc - enc_right) * pi * D / (4096 * 7.5) # dleft is left boot positon dleft = (left_enc - enc_left) * pi * D / (4096 * 7.5) enc_right = right_enc enc_left = left_enc dxy_ave = (dright + dleft) / 2.0 dth = (dright - dleft) / wheel_track vxy = dxy_ave / dt vth = dth / dt rospy.loginfo('dxy_ave = %f', dxy_ave) if dxy_ave != 0: dx = cos(dth) * dxy_ave dy = -sin(dth) * dxy_ave x += (cos(th) * dx - sin(th) * dy) y += (sin(th) * dx + cos(th) * dy) if dth != 0: th += dth rospy.loginfo('x = %f, y = %f' % (x, y)) quaternion = Quaternion() quaternion.x = 0.0 quaternion.y = 0.0 quaternion.z = sin(th / 2.0) quaternion.w = cos(th / 2.0) # Create the odometry transform frame broadcaster. odomBroadcaster.sendTransform( (x, y, 0), (quaternion.x, quaternion.y, quaternion.z, quaternion.w), rospy.Time.now(), base_frame, # sub-ordi "odom" # farthe-ordi ) odom = Odometry() odom.header.frame_id = "odom" odom.child_frame_id = base_frame odom.header.stamp = now odom.pose.pose.position.x = x odom.pose.pose.position.y = y odom.pose.pose.position.z = 0 odom.pose.pose.orientation = quaternion odom.twist.twist.linear.x = vxy odom.twist.twist.linear.y = 0 odom.twist.twist.angular.z = vth odomPub.publish(odom)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号