64. Minimum Path Sum
- 思路1
刚看到这道题的时候,第一个思路还是DFS,但是考虑到前面几个问题,怕DFS超时,所以直接使用DP。
- 思路2 动态规划
题目中给出输入样例为:

DP需要维护一个二维数组,dp[i][j]表示到(i,j)的最短的路径和。
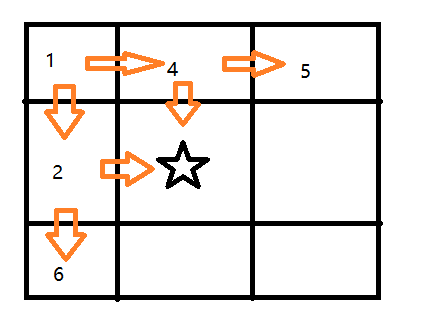
首先看两条边,两条边的走法比较单一,只能横着走过去或者竖着向下走,因此dp[i][j] = dp[i][j - 1] + grid[i][j]或dp[i][j] = dp[i - 1][j] + grid[i][j]。
当初始化完dp数组的两条边后,考虑图中标记五角星的地方,五角星可以横着走过去或者向下走过去,但是要考虑这两种走法那种路径和比较小。,因此五角星地区的状态转移方程为:dp[i][j] = min(dp[i - 1][j] + grid[i][j],dp[i][j - 1] + grid[i][j])。
C++代码实现:
class Solution
{
public:
int minPathSum(vector<vector<int>>& grid)
{
int row = grid.size();
int col = grid.at(0).size();
int i, j;
//声明一个dp数组
vector<vector<int>> dp(row, vector<int>(col));
for (i = 0;i < row;i++)
{
for (j = 0; j < col; j++)
{
dp[i][j] = grid[i][j];
}
}
for (i = 0;i < 1;i++)
{
for (j = 1;j < col;j++)
{
dp[i][j] = dp[i][j - 1] + grid[i][j];
}
}
for (j = 0; j < 1; j++)
{
for (i = 1; i < row; i++)
{
dp[i][j] = dp[i - 1][j] + grid[i][j];
}
}
//根据状态转移方程求解
for (i = 1;i < row; i++)
{
for ( j = 1; j < col; j++)
{
dp[i][j] = min(dp[i - 1][j] + grid[i][j],dp[i][j - 1] + grid[i][j]);
}
}
return dp[row - 1][col - 1];
}
};




 浙公网安备 33010602011771号
浙公网安备 33010602011771号