62. Unique Paths
- 思路1
这个思路比较简单,就类似于图的遍历算法,用递归来解。递归的基线条件是到达目的地或者是走到了边界。递归的条件是机器人从一个点只能往下走或者往右走,即x = x + 1或者y = y+1。到达某一格的路径数量等于它的上面和左边的路径数之和。
C语言实现
int DFS(int x,int y,int m,int n)
{
if (x > m || y > n)
{
return 0;
}
if (x == m && y == n)
{
return 1;
}
return DFS(x+1,y,m,n) + DFS(x,y+1,m,n);
}
int uniquePaths(int m, int n)
{
return DFS(1,1,m,n);
}
但是上面代码在LeetCode上运行,会提示Time Limit Exceeded。
- 思路2 DP
采用动态规划思路需要维护一个二维数组dp[][], dp[i][j] 表示到当前位置不同的走法的个数,然后可以得到状态转移方程为: dp[i][j] = dp[i - 1][j] + dp[i][j - 1],注意在初始化的时候,要把二维数组的两个边全部初始化为1,如下图:
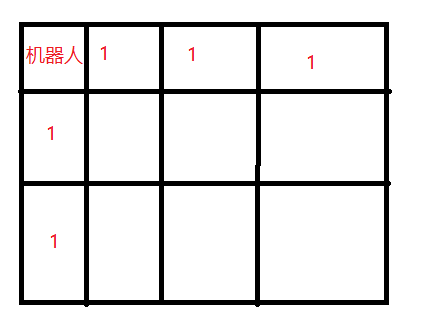
这是因为,机器人到这些地点的走法只有一种,只能顺着边走。
下面这张图显示了使用DP解法的时候,需要维护的dp[][]数组。
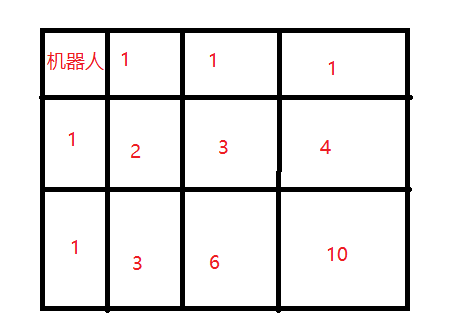
C++代码实现
class Solution
{
public:
int uniquePaths(int m, int n)
{
if (m <= 0 || n <= 0)
{
return 0;
}
//维护一个二维数组
vector<vector<int>> dp(m);
for (int k = 0;k < m;k++)
{
dp[k].resize(n);
}
int i = 0;
int j = 0;
for (i = 0;i < m;i++)
{
for (j = 0;j < n;j++)
{
dp[i][j] = 1;
}
}
for (i = 1;i < m;i++)
{
for (j = 1;j < n;j++)
{
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; //状态转移方程
}
}
return dp[m - 1][n - 1];
}
};




 浙公网安备 33010602011771号
浙公网安备 33010602011771号