古堡朝圣问题与椭圆的光学性质

第一次接触到古堡朝圣问题是在初三.

我的一个同学从一道几乎与之无关的初中数学题中提取出来了这个问题.当时的我们不知道这个问题的名字,并且对于椭圆没什么了解,只是想着能推出多少算多少,最后得到了一个似乎不能很好地解决该问题的方法.到了高中意外的发现居然可以由它推出椭圆的光学性质,便打算记录下来,并以此纪念过去的中学时光.

古堡朝圣问题:从前有一个虔诚的信徒,他是集市上的一个小贩,每天他都从家所在的\(C\)点出发,到集市\(D\)点做买卖.到集市之前他要先拐弯到圆形古堡朝拜阿波罗神像.圆形古堡是座圣城,阿波罗像供奉在古堡的圆心\(A\)点上,而圆周上的点都是供信徒朝拜的顶礼点.请问这个信徒应该选择什么样的顶礼点,才能从家到顶礼点,然后再到集市的路程最短呢？

在圆上取一点命名为\(E\),若点\(E\)满足\(\angle CEA=\angle DEA\),则\(E\)点即为答案.

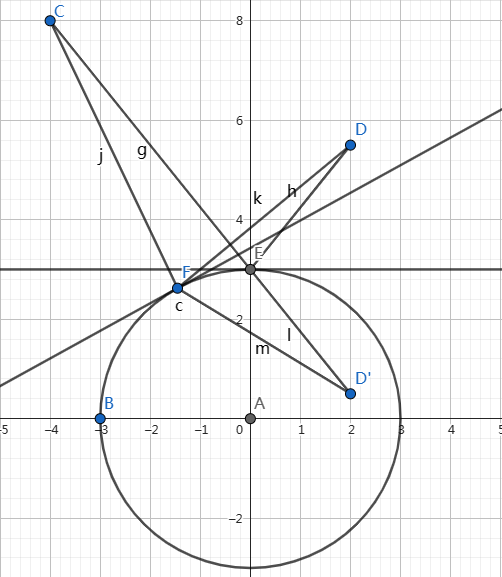
证明:作\(E\)关于圆\(A\)的切线,作\(D\)关于该切线的对称点\(D'\).设\(F\)为圆上,连接\(FD'\).

因为\(E\)点切线为\(DD'\)中垂线,所以\(D'F<DF\).

\(DE+EC=D'E+EC=D'C<D'F+FC<DF+FC\).

证毕.

我们还有一种方法可以找到这个点.因为\(C,D\)两点固定,我们可以以这两个点作为焦点作一个椭圆,该椭圆\(c\)不变,椭圆越小\(a\)越小.因此当椭圆恰好与圆相切时,切点即为答案.

不难发现,该切点的切线同时是椭圆和圆的切线,由此我们证明了椭圆的光学性质.

椭圆的的光学性质:从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上.

这是一个推导过程和我基本一样的文章,但似乎它并没有意识到这可以用来证明椭圆的光学性质.只不过初中的我是通过它了解到的该问题的名字并知道了自己证明的正确性的.

当然不难发现该方法也可以推导出双曲线的光学性质.