插入排序

插入排序

之前的文章讲过选择排序和冒泡排序，他们都有各自的优缺点，比如选择排序不稳定，冒泡排序效率较低等。这次我们来聊一聊简单排序中的最后一种——插入排序，相比于选择排序和冒泡排序，是更为常用的简单排序，在样本小且基本有序的时候效率比较高。
插入排序的基本思想每次从无序数组中取一个值然后插入到有序数组的相应位置中，直至无序数组中的所有元素都插入到有序数组的相应位置为止，在代码实现时我们会先把第一个元素作为有序数组(单个元素不存在无序问题)，然后从第二个元素开始往后逐个的将值插入到前面的有序数组中构成新的有序数组，如此循环往复，直至数组末尾元素插入到有序数组中为止。
假定初始数组为：{4,1,3,2,5}

第一轮插入排序将索引为1的第二个元素值1插入到有序数组{4}中构成{1,4}之后得到的数组为{1,4,3,2,5}

第二轮插入排序将索引为2的第三个元素值3插入到有序数组{1,4}中构成{1,3,4}之后得到的数组为{1,3,4,2,5}

第三轮插入排序将索引为3的第三个元素值2插入到有序数组{1,3,4}中构成{1,2,3,4}之后得到的数组为{1,2,3,4,5}

第四轮插入排序将索引为5的第四个元素值5插入到有序数组{1,2,3,4,5}中得到最终排序结果为{1,2,3,4,5}

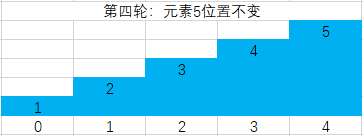
对应的算法代码为：

static void insertion1(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        int index = 0, temp = arr[i];
        for (int j = i - 1; j >= 0; j--) {
            if (arr[j] <= temp) {      //找到第一个小于等于待插入值的索引位置
                index = j + 1;         //记录下一个索引位置，该位置即为插入位置
                break;
            }
        }
        System.arraycopy(arr, index, arr, index + 1, i - index);//将插入位置后的有序元素向后移动一个位置
        arr[index] = temp;//插入位置插入元素
    }
}

上述的方法为找到待插入元素应处于的有序数组的索引位置后，通过将有序数组中相应位置之后的所有元素向后移动一个位置将指定索引位置空出来之后再将待插入元素插入，该算法的实现相对麻烦一点，下面一种方法则有点冒泡排序的思想，将待插入值冒泡(逐个交换)到应处位置，对应的算法为：

static void insertion2(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        for (int j = i; j > 0 && arr[j - 1] > arr[j]; j--) {//每次都与前一个值进行比较，如果前一个值大于待插入值，则进行交换
            Utils.swap(arr, j - 1, j);
        }
    }
}

测试排序结果

通过对数器的方式进行排序结果的验证

//测试代码
public static void main(String[] args) {
    int size = 15;
    int[] arr1 = Utils.generateRandomArray(size, 100);
    int[] arr2 = new int[size];
    System.arraycopy(arr1, 0, arr2, 0, size);
    int[] arr3 = new int[size];
    System.arraycopy(arr1, 0, arr3, 0, size);
    System.out.println("原数组：\t\t\t" + Arrays.toString(arr1));
    Arrays.sort(arr1);
    System.out.println("系统方法排序后：\t" + Arrays.toString(arr1));
    insertion1(arr2);
    System.out.println("插入方法1排序后：\t" + Arrays.toString(arr2));
    insertion2(arr3);
    System.out.println("插入方法2排序后：\t" + Arrays.toString(arr3));
}

原数组：		[54, 73, 99, 99, 93, 44, 72, 32, 77, 80, 55, 99, 3, 49, 77]
系统方法排序后：	[3, 32, 44, 49, 54, 55, 72, 73, 77, 77, 80, 93, 99, 99, 99]
插入方法1排序后：	[3, 32, 44, 49, 54, 55, 72, 73, 77, 77, 80, 93, 99, 99, 99]
插入方法2排序后：	[3, 32, 44, 49, 54, 55, 72, 73, 77, 77, 80, 93, 99, 99, 99]

如果对你有帮助，点个赞，或者打个赏吧，嘿嘿
整理不易，请尊重博主的劳动成果