HDU1517 A Multiplication Game (博弈论+思维)

 
题目链接:传送门
 
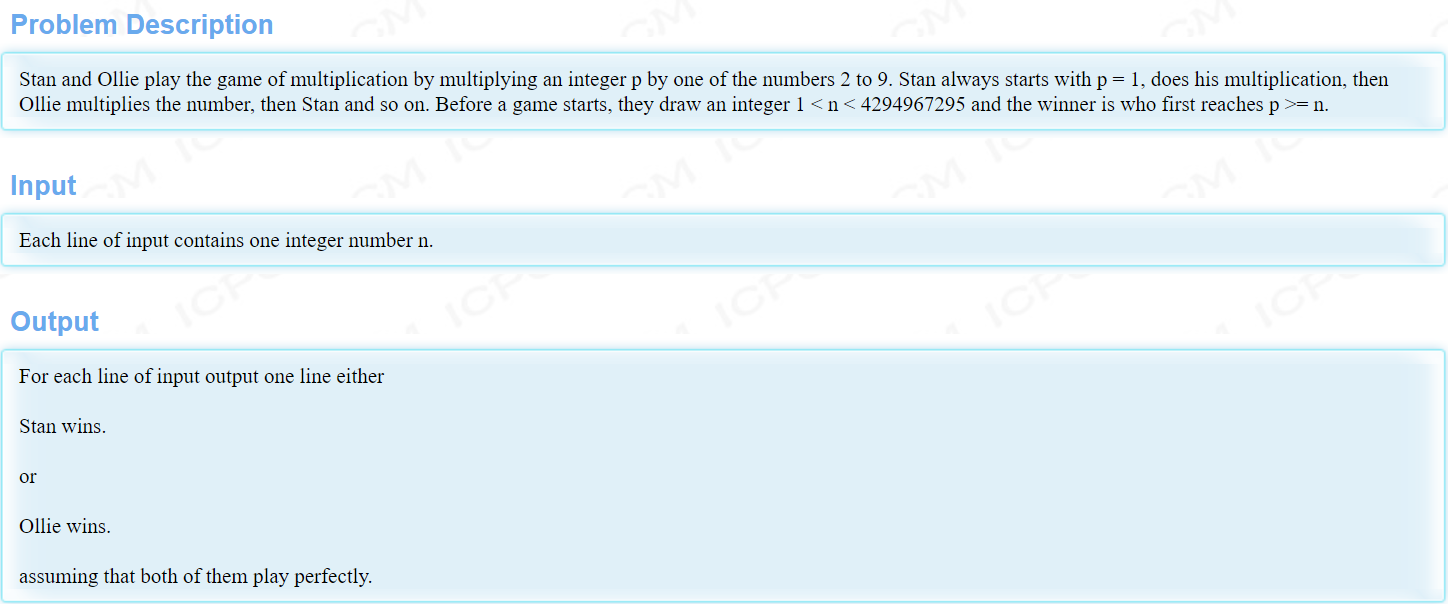
题意:两个人玩游戏，给定一个数n，从1开始，轮流对该数累乘，直到该数大于等于n结束，Stan每次都先手
 
解题思路:很明显我们可以发现当n为[2,9]的时候，Stan必胜，当n为[10,18]的时候，无论Stan输入了什么，Ollie都能乘以一个[2,9]的数使得当前的数大于等于n，换句话说也就是在n为[10,18]是Ollie的必胜区间，一次类推我们会发现当n为[19,162]的时候，是Stan的必胜区间，当n为[163,324]的时候是Ollie的必胜区间，换句话说也就是说两位的必胜区间都是交替进行的，每18一个周期，我们只需要判断n不断除18后余下的m的值是多少即可判断是谁必胜，当m为[2，9]时，Stan必胜，当m为[10,18]时，Ollie必胜,注意n用double类型，因为在对n不断进行18除的时候此时的n不一定时18的倍数，这样会造成数据的丢失，会对结果造成影响
 
Code:

#include<cstdio>
main(double t)
{
	while(~scanf("%lf",&t)) {
		while(t > 18)t = t/18;
		t<=9?puts("Stan wins."):puts("Ollie wins.");
	}
}