Home_W的几何题 (计算几何)

题目链接:传送门
 
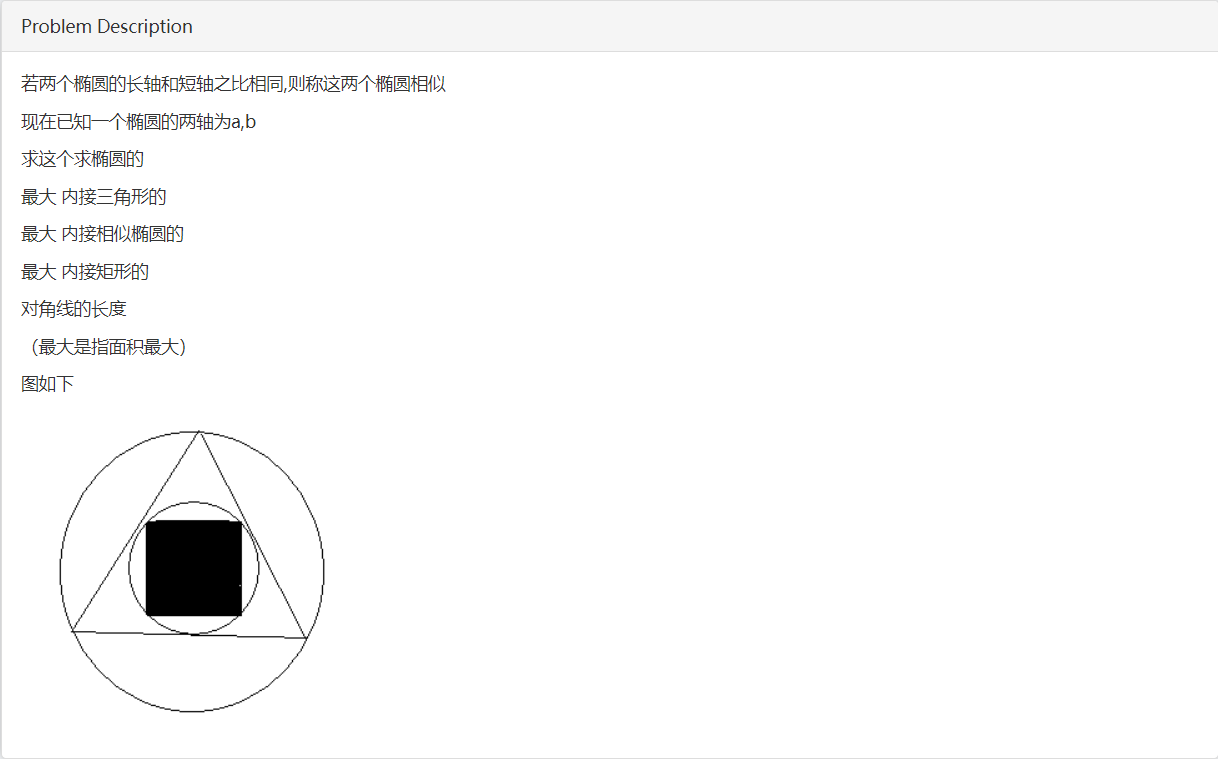
解题思路:主要用到的知识点是仿射变换，一种巧妙的方法，我们先是对椭圆做仿射变换，得到变换后的圆的半径为a，我们对变换后的圆可以取得最大的内接三角形是以边为\(\sqrt3a\)的等边三角形，我们再分析可得最大内接圆的半径为\(\frac{a}{2}\)，该圆的最大内接矩形是边长为\(\frac{\sqrt2a}{2}\),然后对矩形进行逆变换，得到边长分别为\(\frac{\sqrt2a}{2}\)和\(\frac{\sqrt2b}{2}\)的矩形，最后求得对角线长度为\(\frac{\sqrt{2 \times (a^2+b^2)}}{2}\)
 
Code:

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	double a,b;
	scanf("%d",&t);
	while(t--) {
		scanf("%lf%lf",&a,&b);
		printf("%.6lf\n",sqrt(2*(a*a+b*b))/2.0);
	}
	return 0;
}