stone (组合数学 + Lucas定理)

 
传送门
 
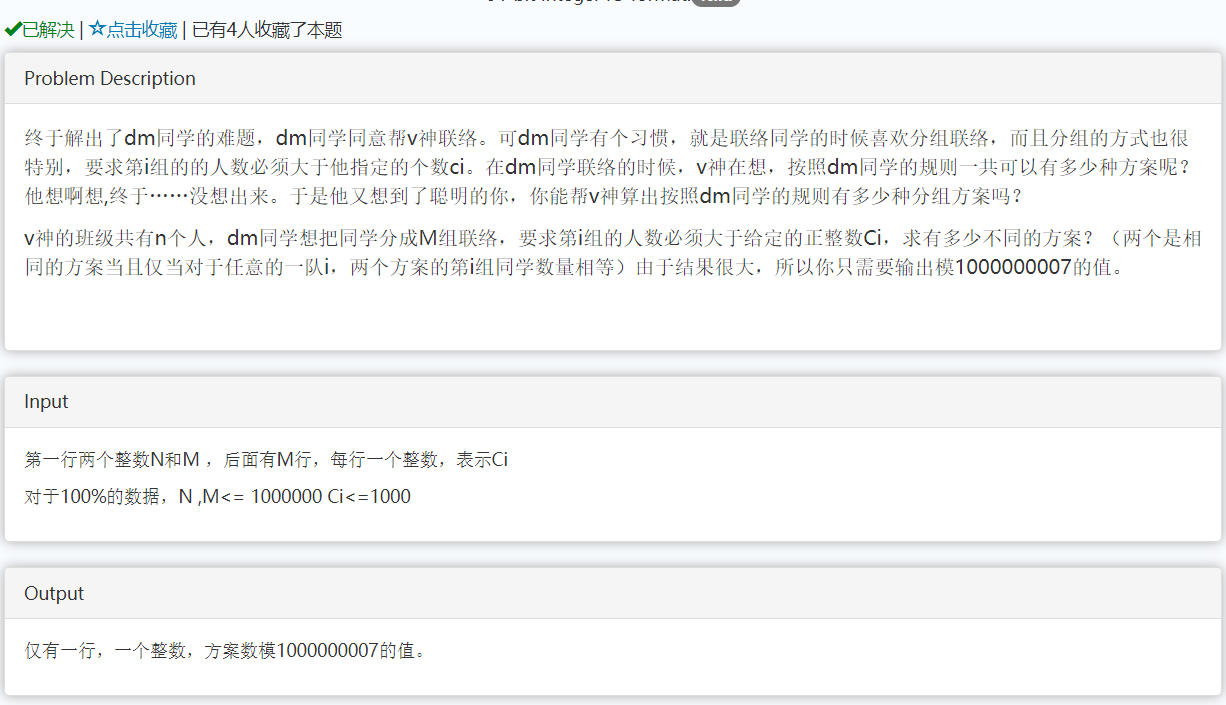
解题思路:第i组的人数必须大于Ci，于是我们可以将问题转化为\(N-\sum_{i=1}^M Ci\)人分到M组中，且保证每一组的人数大于0，然后我们可以使用隔板法求出分的的组数\(C_{N-1-\sum_{i=1}^M Ci}^{m-1}\)
我们可以直接通过基本的组合公式+费马小定理直接求，也可以通过Lucas定理求得:
直接求:
Code:

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
ll n,m,a,t;

ll power(ll a,ll b) {
	ll ans = 1;
	while(b) {
		if(b&1) ans = (ans*a)%mod;
		a = (a*a)%mod;
		b>>=1;
	}
	return ans;
}

ll inv(ll x) {
	return power(x,mod-2);
}

ll C(ll a,ll b) {
	ll ans =  1;
	for(ll i = 1;i <= b; ++i) {
		ans = (ans*(a-i+1)) % mod;
		ans = (ans*inv(i)) % mod;
	}
	return ans % mod;
}

int main()
{
	while(~scanf("%lld%lld",&n,&m)) {
		a = 0LL;
		for(int i = 0;i < m; ++i) {
			scanf("%lld",&t);
			a += t;
		}
		printf("%lld\n",C(n-a-1,m-1));
	}

	return 0;
}

 
Lucas定理:

#include <iostream>
#include <cstdio>
using namespace std;

#define MOD 1000000007
typedef long long LL;

int Read() { //快读
	char c; int ans(0);
	while(!isdigit(c = getchar()));
	do ans = ans * 10 + c - 48;
	while(isdigit(c = getchar()));
	return ans;
}

int n, m;

LL Qpow(LL a, LL b, LL p) { //快速幂 
	LL ans = 1;
	for(; b; b>>=1, (a*=a) %= p)
		if(b & 1) (ans *= a) %= p;
	return ans;
}

LL c(LL n, LL m, LL p) {
	if(n < m) return 0;
	if(m > n - m) m = n - m;
	LL s1 = 1, s2 = 1;
	for(int i=0; i<m; i++) {
		s1 = s1 * (n - i) % p;
		s2 = s2 * (i + 1) % p;
	}
	return s1 * Qpow(s2, p-2, p) % p;
}

LL Lucas(LL n, LL m, LL p) { //Lucas
	if(m == 0) return 1;
	return c(n % p, m % p, p) * Lucas(n / p, m / p, p) % p;
}

int main() {
	n = Read(), m = Read();
	for(int i=1; i<=m; i++) n -= Read();
	printf("%d\n", Lucas(n-1, m-1, MOD));
	return 0;
}