吉首大学第十届“新星杯”大学生程序设计大赛(暨新生网络同步赛)
部分题解
前言
下午在群里面看到一个同学疯狂宣传这个比赛,处于好奇的态度(他说难度有cf1800)我参赛了,可能真的有cf1800的题目,只是我没做出来,离比赛还有十多分钟的时候到了吉首的OJ,注册了账号,稍稍等待之后进入了比赛,出于习惯开了A题,然后想了几分钟没有思路,然后切出去看榜单,看见有人过了J题,我赶紧开了J题,嗯,是个签到题,但是WA了一发,读题的时候漏掉了一个信息,改了后A了,然后开了C,立方和公式稍微一化简就能找到a和b和n的关系,然后一发A了,接着开了E,一发A,刷了下榜单,看到L过了十多人,第一发处理边界的时候出了问题,后面想了下可以直接O(N)扫过去找到最小的,第三发A了,然后此时我在20名左右(暂时靠前),于是又回去看A,稍微想了一下然后又写了个公式,然后自己测试都没过,于是我开始直接硬推公式,想了二十多分钟还是没想出来,于是我开始打表找找规律,在反复观察后,我发现了一个规律,但是当时睡意来了,看着面前的屏幕还有外面刺眼的光线,我的眼睛开始疼痛,强忍着,继续记录规律,在二十多分钟后我把规律转化为了公式,然后交上去第一发CE(本地是能跑的),我把头文件换成了万能头,交上去一发A了,从这一发A之后后面就做的太难受了,接着我开了D,很明显D是一个模拟题,但是一直写不对(写代码细节没写好),然后转身开了F,感觉是一个博弈论,第一发我直接交了cxy上去,然后过了一半的测试点,接着交了几法rand,没过就没看了,然后这个时候我发现K题有几十人切出来了,于是赶忙去切K,由于我的粗心,计算的时候写反了,贡献了5发罚时,此时已经是四点五十二了,最后转身去开D,在贡献了20发罚时的情况下,在最后的5分钟把D题A了,当时激动的喊了出来(^^)。
A: 学习快速幂
传送门
众所周知,快速幂是一个很重要的算法,相比朴素算法,可以更加快速的求解形如(ab)%c的问题(ab意思是a的b次幂),此算法的时间复杂度是log级别的。
现在相信你已经会快速幂算法了,今天你的同学zcb来问你他这段快速幂代码是不是正确的,他的快速幂写的是递归形式的,虽然之前你没学过,但是看了两眼还是立马发现了问题所在。程序运行是正确没错,但是有个地方没有优化,导致时间复杂度并不能过关。
如下,给你这段快速幂代码,为了证明zcb的代码有问题,请你算出他的代码的复杂度以证明zcb的递归有问题。为了更加有说服力,给你一个数n,你需要算出此代码在计算a0,a1,a2…an,的复杂度的和。因为显然a与本题复杂度计算无关,所以并不给出a的值。
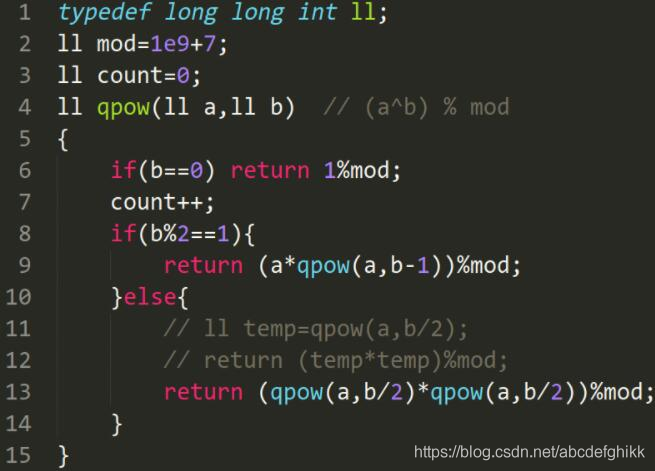
图中11,12行的注释代码为你认为的正确写法,不过与本题并无关系,在这题中,我们定义在递归结束后count的值为一次求快速幂的复杂度,比如计算a0,a1,a^2分别需要0,1,3的复杂度。
输入
首先输入一个t,代表有t组输入(1<=t<=1e5)
接着每组输入给你一个数n(0<=n<=1e9)
本题请使用scanf printf输入输出
输出
对于每组输入,你需要算出此代码在计算a0,a1,a2…an,的复杂度的和。
样例输入
3
0
1
2
样例输出
0
1
4
解题思路:通过打标找规律我们能发现,复杂度从\(2^{i}-1\)开始到\(2^{i}-1+2^{i-1}\)是连续的,然后通过两次求和可以算出公式
退出公式后我们就可以直接写代码啦^^
Code:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007;
int cnt = 0;
ll qpow(ll a, ll b) {
if(b == 0) {
return 1%mod;
}
cnt++;
if(b%2 == 1) {
return (a*qpow(a,b-1))%mod;
}
else {
return (qpow(a,b/2)*qpow(a,b/2))%mod;
}
}
long long f(int n) {
long long ans = 0;
while(n) {
n/=2;
ans++;
}
return ans;
}
ll cal(ll n) {
ll ans = (ll)pow(2,n-1) * (ll) (pow(2,n)-1) + ((ll)pow(2,n-1)-1)*((ll)pow(2,n-1))/2;
return ans;
}
ll cal2(ll k, ll len) {
ll ans =len * (ll)(pow(2,k)-1) + (len-1LL)*len/2;
return ans;
}
int main()
{
int t;
// for(int i = 0;i < 5; ++i) {
// cnt = 0;
// qpow(1,i);
// printf("%d\n",cnt);
// }
scanf("%d",&t);
int n;
while(t--) {
scanf("%d",&n);
if(n == 0) {
puts("0");
continue;
}
long long k = f(n);
ll ans = 0;
for(ll i = 1;i <= k - 1; ++i) {
ans += cal(i);
}
ll len = max(0LL,n - (ll)(pow(2,k-1)-1));
ans += cal2(k,len);
printf("%lld\n",ans);
}
return 0;
}
B: 算数之王
给你一堆随机的卡牌,从中取出两组卡牌(不能重复取),要求这两组的卡牌点数之和相等,请问有多少种取法,在所有的取法中每组最大的点数为多少,每组点数和相同视为同一种方案。为了方便,卡牌点数统一用1-13(A-K)的数字表示。
输入数据
第一行输入一个整数T,代表测试数据组数(1<=T<=100)
每组数据分成两行,第一行输入正整数n(n<=10)为卡牌张数,第二行为每张卡牌的点数。
输出数据
共一行,输出方案数和所有合法方案中最大每组点数之和(以空格分开)。没有合法取法,则输出0 0。
注意是0 0
样例输入
1
6
1 3 4 2 3 5
样例输出
7 9
hint
1)1 2 和 3
2)1 3 和 4
3)1 4 和 5
4)1 5 和 2 4或
3 3 和 2 4或
3 3 和 1 5
5)2 5 和 3 4
6)1 3 4 和 3 5
7)1 2 3 3 和 4 5
共7种方案,所有合法方案中,最大每组点数和为9
Code
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int a[20];
int vis[20],b[200];
int f,sum,n,t,ans;
void dfs(int ret,int s)
{
if(s>sum)
return;
if(s==sum)
{
f=1;return;
}
for(int i=ret+1;i<n;++i)
{
if(vis[i]==1)
continue;
dfs(i,s+a[i]);
if(f==1)
return;
}
}
void df(int ret)
{
for(int i=ret+1;i<n;++i)
{
vis[i]=1;
sum+=a[i];f=0;
for(int j=0;j<n;++j)
if(vis[j]==0)
dfs(j,a[j]);
if(f){
b[sum]=1;ans=max(ans,sum);
}
df(i);
sum-=a[i];
vis[i]=0;
}
}
int main()
{
cin>>t;
while(t--)
{
memset(b,0,sizeof(b));
int ret=0;
ans=0;
cin>>n;
for(int i=0;i<n;++i)
cin>>a[i];
for(int i=0;i<n;++i)
{
memset(vis,0,sizeof(vis));
sum=a[i];
f=0;vis[i]=1;
for(int j=0;j<n;++j)
if(vis[j]==0)
dfs(j,a[j]);
if(f){
b[sum]=1;ans=max(ans,sum);
}
df(i);
}
for(int i=0;i<200;++i)
if(b[i]==1)
ret++;
cout<<ret<<" "<<ans<<endl;
}
}
C: LeeLdler的数字
有一天LeeLdler偶然发现一个规律
像这种形如(n3+a3 )/(n3+b3)=(n+a)/(n+b)有很多种
现在LeeLdler给出一个数字n,请找出任意一对不相等的正整数a,b满足上述等式.
输入
输入一个正整数n(3<=n<=10^9)
输出
输出两个正整数a,b,以空格隔开. a!=b,且a,b都在int范围内.
答案可能存在多组,输出任一组即可
样例输入
5
样例输出
2 3
解题思路:把立方和化简一下,我们就能得到a+b=n这个结论,所以随便交一个正整数数据满足之和尾n就行
Code:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
scanf("%d",&n);
printf("%d %d\n",n-1,1);
return 0;
}
D: 珍爱生命,远离赌博
zqc和lbg是实验室的两个赌徒,有一天他们把钱都输给了prz之后就想起了用牌来玩一个小游戏来练练自己的牌技。zqc先抽一张牌,亮出在桌面上,然后lbg抽一张牌放在上一张牌后面,依此放牌,如果放的这张牌和之前的某张牌点数相同则可以取走这两张相同点数牌以及他们之间的牌(A到K牌的分数为1到12),牌的大小顺序:A<2<3<4<5<6<7<8<9<J<Q<K,没有大小王。请你求出谁赢了,并且输出赢的人的分数。最终桌上剩下的牌忽略不计,如果最终两人分数相同则输出-1。两人的分数即他们整个过程取走的牌的分数之和。
输入
输入一个字符串s(字符串不为空且长度最长不超过2e6),表示他们完整放牌的过程。
输出
输出一行,赢的人和赢的人的分数。
样例输入
A23456789JQK4A
样例输出
zqc 76
解题思路:我们可以开一个map作为标记,标记这张牌在之前的位置是否出现,然后开一个栈存放牌,输入一个字符串,我们遍历这个字符串,如果发现即将要放进去的这张牌在之前出现过,那么一定在栈中有相同的元素,我们直接对栈开始pop操作直到找到这个元素为止,在pop的过程中别忘了把这些元素的vis清除,如果将要放进去的字符串没有出现过那么久入栈,并且标记该元素已经出现过。注意的是,这题好像卡了常数,我的做法在复杂度上是\(O(N)\)的。
Code:
#define fastcall __attribute__((optimize("-O3")))
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")//这是优化常数的代码
#include<bits/stdc++.h>
using namespace std;
unordered_map<char,bool> vis;
unordered_map<char,int> mp;
char ch[2000006];
stack<char> S;
int main()
{
// string str;
// cin>>str;
scanf("%s",ch);
mp['A'] = 1;mp['2'] = 2;mp['3'] = 3;mp['4'] = 4;mp['5'] = 5;mp['6'] = 6;mp['7'] = 7;mp['8'] = 8;mp['9'] = 9;mp['J'] = 10;mp['Q'] = 11;mp['K'] = 12;
int l = 0, r = 0;
for(int i = 0,len = strlen(ch);i < len; ++i) {
if(vis[ch[i]]) {//S.size() &&
if(i & 1) {
while(S.size() && S.top() != ch[i]) {
vis[S.top()] = false;
r += mp[S.top()];
S.pop();
}
// r += 2 * mp[ch[i]];
if(S.size()) {
r += 2*mp[S.top()];
S.pop();
}
}
else {
while(S.size() && S.top() != ch[i]) {
vis[S.top()] = false;
l += mp[S.top()];
S.pop();
}
//l += 2 * mp[ch[i]];
if(S.size()) {
l += 2 * mp[S.top()];
S.pop();
}
}
vis[ch[i]] = false;
continue;
}
S.push(ch[i]);
vis[ch[i]] = true;
}
if(l == r) {
puts("-1");
}
else {
if(l < r) {
printf("lbg %d\n",r);
}
else
printf("zqc %d\n",l);
}
}
E: 会长的榜单
众所周知,每场ACM比赛都有排名榜单,上面会显示每个队的过的题和过题时间,每次给20级的新生们上机辅导的时候会长都会坐在讲台上看榜单,其实会长看到的榜单和大家看到的是不一样的,正常的榜单的过题时间是小时加分钟(比如:XX:XX:XX,或者看图),而会长看到的过题时间是以秒为单位的(比如正常榜单的01:00:00,会长看到的是3600)。这次新星杯网络赛会长还是会一如既往的坐在讲台上看榜单,但是会长最近由于期末周复习,脑子用太多了,换算不过来了,聪明的你能帮帮会长吗?
输入
输入两行
第一行一个整数 n 代表本场题目数量(1<=n<=10)
第二行一个字符串代表某一位选手的榜,格式为选手昵称(不超过10个字符)和各个题目的过题时间;
如果这题没通过,时间显示为0(众所周知不可能有人0s过题)
一场ACM比赛时间为5小时
输出
输出一行表示这位选手的榜换算成正常显示时间的榜单,(未通过的题目依旧显示0即可)
样例输入
10
顺十字 3600 3660 7200 300 0 1500 2600 4561 2345 8945
样例输出
顺十字 01:00:00 01:01:00 02:00:00 00:05:00 0 00:25:00 00:43:20 01:16:01 00:39:05 02:29:05
解题思路:这题就是把秒数转化为小时、分钟、秒数进行表示,如果该秒数为0则直接输出0
Code:
#include<bits/stdc++.h>
using namespace std;
const int N = 20;
int a[N];
int h[N];
int m[N];
int s[N];
int main()
{
char name[30];
int n;
cin>>n;
cin>>name;
for(int i = 0;i < n; ++i) {
cin>>a[i];
h[i] = a[i] / 3600;
a[i] -= h[i] * 3600;
m[i] = a[i] / 60;
a[i] -= m[i] * 60;
s[i] = a[i];
}
printf("%s ",name);
for(int i = 0;i < n; ++i) {
if(h[i] == 0 && m[i] == 0 && s[i] == 0)
printf("0%c",i ==n-1?'\n':' ');
else
printf("%02d:%02d:%02d%c",h[i],m[i],s[i],i ==n-1?'\n':' ');//格式化输出
}
}
I: 广告(天梯打钱)
团体程序设计天梯赛是中国高校计算机大赛的竞赛版块之一,其规则为10人为1队,竞赛题目分 3 个梯级:基础级设 8 道题,其中 5 分、10 分、15 分、20 分的题各 2 道,满分为 100 分;进阶级设 4 道题,每道题 25 分,满分为 100 分;登顶级设 3 道题,每道题 30 分,满分为 90 分,共15道题。参赛队员可以在比赛中的任何时刻尝试解决任何梯级的题目。但只有当一支队伍的基础题总分大于等于 800 分时,其本队进阶部分的题目分数才被判为有效。只有当其进阶题总分大于等于 400 分时,其本队登顶部分的题目分数才被判为有效。现给出n支队伍的比赛情况,要求你给n支队伍按照有效分数从高到低排好序,如果分数相同则按照队伍ID的升序输出,并且最后一行输出n支队伍中的最高分和所有优胜者(分数最高者,个人分数不受团队影响)的ID(按照ID的升序)
(队员计分根据过题的数据比例计算,也就是说不一定都是0分和满分)
输入
第一行输入一个数字n(1<=n<=100),之后11*n行分别输入每支队伍的ID(长度为1到10),每支队伍队员的ID(长度为1到10)和得分情况(按照基础题到登顶题的顺序输入,题目分值分别为5,5,10,10,15,15,20,20,25,25,25,25,30,30,30),保证队员、队伍ID都不重复。
输出
按照题目要求顺序输出队伍ID和3个阶段的分数和有效总分以及排名(分数相同排名相同,例:A,B,C三支队伍总分分别为1500,1500,1000,排名为A:1,B:1,C:3),最后一行输出个人最高分和所有优胜者的ID(按照ID的升序)
样例输入
2
JSU0001
000001 5 5 10 10 15 15 20 20 25 25 25 0 30 0 0
000002 5 5 10 10 15 15 20 20 25 25 0 0 0 0 0
000003 5 5 10 10 15 15 20 20 25 25 15 0 0 0 0
000004 5 5 10 10 15 15 20 20 25 10 0 0 0 0 0
000005 5 5 10 10 15 15 20 20 25 0 25 0 0 0 0
000006 5 5 10 10 15 15 20 20 10 25 25 0 20 0 0
000007 5 5 10 10 15 15 20 20 15 0 25 0 0 0 0
000008 5 5 10 10 15 15 20 20 25 0 25 0 0 0 0
000009 5 5 10 10 15 15 20 20 25 10 25 0 0 0 0
000010 5 5 10 10 15 15 20 20 0 25 25 0 0 0 0
JSU0002
000011 5 5 10 10 15 15 20 20 0 25 25 0 30 30 30
000012 5 5 10 10 15 15 20 20 0 25 25 0 0 0 0
000013 5 5 10 10 15 15 20 20 0 0 0 0 0 0 0
000014 5 5 10 10 15 15 20 20 0 25 0 0 0 0 0
000015 5 5 10 10 15 15 20 20 0 0 25 0 0 0 0
000016 5 5 10 10 15 15 20 20 0 0 25 0 0 0 0
000017 5 5 10 10 15 15 20 20 0 25 0 0 0 0 0
000018 5 5 10 10 15 15 20 20 0 0 0 0 0 0 0
000019 5 5 10 10 15 15 20 20 0 0 25 0 0 0 0
000020 5 5 10 10 15 15 20 20 0 25 0 0 0 0 0
样例输出
JSU0001 1000 535 50 1585 1
JSU0002 1000 250 90 1250 2
240 000011
解题思路:
结构体排序的题,思路很简单,注意几个细节问题就好,队伍计分必须要基础题大于等于 800 分才可计算进阶级的分,并且进阶级的分大于等于 400 分才计算团队的登顶级分数。分数相同时按照队伍 ID 的字典序从小到大排序,尤其注意排名要特殊处理分数相同排名相同,分数不同则按照名次计算排名,如 A,B,C分数 1500,1500,1000,排名为 A:1,B:1,C:3。然后就是输出分数最高的(同样按照ID 字典序从小到大排序)
Code
#include <bits/stdc++.h>
using namespace std;
struct people {
string name;
int score[20], a, b, c, s;
void read() {
cin >> name;
s = 0;
for (int i = 1; i <= 15; i++) cin >> score[i], s += score[i];
a = b = c = 0;
for (int i = 1; i <= 8; i++) a += score[i];
for (int i = 9; i <= 12; i++) b += score[i];
for (int i = 13; i <= 15; i++) c += score[i];
}
};
vector<people> all;
struct team {
string name;
people p[15];
int a, b, c, s, id, rank;
void read() {
cin >> name;
a = b = c = 0;
for (int i = 1; i <= 10; i++) {
p[i].read();
all.push_back(p[i]);
a += p[i].a;
b += p[i].b;
c += p[i].c;
}
s = a;
if (a >= 800) s += b;
if (a >= 800 && b >= 400) s += c;
}
} a[105];
bool cmp1(team a, team b) {
return a.s == b.s ? a.name < b.name : a.s > b.s;
}
bool cmp2(people a, people b) {
return a.name < b.name;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
for (int i = 1; i <= n; i++) a[i].read(), a[i].id = i;
sort(a + 1, a + n + 1, cmp1);
for (int i = 1; i <= n; i++) {
a[i].rank = i;
if (a[i].s == a[i - 1].s) a[i].rank = a[i - 1].rank;
}
for (int i = 1; i <= n; i++) cout << a[i].name << " " << a[i].a << " "<< a[i].b << " "<< a[i].c <<" "<< a[i].s <<" "<< a[i].rank << endl;
int mx = 0;
sort(all.begin(), all.end(), cmp2);
for (int i = 0; i < all.size(); i++)
mx = max(mx, all[i].s);
cout << mx <<" ";
for (int i = 0; i < all.size(); i++)
if (all[i].s == mx) cout << all[i].name <<" ";
cout << endl;
return 0;
}
J: 会长数
传送门
会长把一个数本身是一个素数、各个数位上的数都是素数、各个数位上的数的和是素数的数叫做会长数,请输出10到100中的所有会长数。
输入
NULL
输出
第一行先输出10-100中会长数的个数,第二行再按从小到大的顺序输出一个会长数,中间按空格隔开,行末无多余空格
解题思路:暴力把数的每一位拿出来判断,并且把这些数的和判断是否是素数,其实满足条件的数只有23
Code:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
bool is_prime(int n) {
if(n==0 || n== 1)
return false;
for(int i = 2;i *i <= n; ++i) {
if(n%i==0)
return false;
}
return true;
}
bool work(int i) {
int ans = 0;
while(i) {
if(!is_prime(i%10))
return false;
ans += i%10;
i/=10;
}
if(is_prime(ans))
return true;
return false;
}
int main()
{
vector<int> V;
for(int i = 10;i <= 100;++i) {
if(is_prime(i) && work(i)) {
V.push_back(i);
}
}
printf("%d\n",V.size());
for(int i = 0, len = V.size();i < len; ++i) {
printf("%d%c",V[i],i == len-1?'\n':' ');
}
return 0;
}
K: 抽奖
斌斌开发了一个抽奖的软件,他请来了小杰和小昭测试抽奖池有没有问题,抽奖池有如下规则
1. 有可能有多件相同的商品
2.一次只能抽一件商品
3. 抽奖池里面商品被抽走后不放回
4. 与当前最大概率的商品 概率 相差 1/5 不会被抽到
即 最大概率商品概率 – 商品概率 > 1/5 不会被抽到
现在小昭测试测试抽奖池,得出了一个抽奖出来的奖品序列;
小杰来判断这个抽奖序列是否满足抽奖池的规则
输入
第一行输入商品种数n ,商品编号依次为 1到n ( 1<=n<=1000)
第二行输入n个数,分别代表每种商品的件数a[i]. (1<=a[i]<=1000)
第三行输入小昭抽奖次数m (1<=m<=1000)
第四行输入小昭依次抽取的m个商品编号b[j](1<=b[j]<=n)
保证第i个商品不会抽取超过a[i]次。
输出
如果满足抽奖池规则 输出PASS ,否则 BUG
样例输入
2
4 5
3
1 1 2
样例输出
BUG
hint
输入解释:
第一行输入2,代表两种商品,商品编号为1和2
第二行输入4 5,代表编号为1的商品有4个,编号为2的商品有5个
第三行输入3,表示小昭依次抽取了3次。
第四行输入1 1 2,表示小昭依次抽到的商品。
输出解释:
小昭第一次抽取的是 商品1,抽取1号商品的概率为 4/9,最大概率商品概率为 5/9,两个概率相差:5/9 - 4/9 = 1/9 <= 1/5,可以被抽取。
第一次抽取结束后,抽奖池中还剩下3个商品1和5个商品2.
小昭第二次抽取的是商品1,抽取1号商品的概率为 3/8,最大概率商品概率为 5/8,两个概率相差:5/8 - 3/8 = 1/4 > 1/5,不满足抽奖池规则,输出BUG。
解题思路:我们先统计商品的总数目,然后每次抽取会让商品的总数目减一,每次找到数目剩下的最多的商品,然后计算概率和当前抽取的商品的概率做差计算差值是否大于1/5,如果大于则表示不满足抽奖池的抽奖规律,做一个标记,最后判断标记是否更改,如果被更改的话,就输出BUG,否则输出PASS,时间复杂度\(O(N^2)\)
Code:
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int a[N];
int n;
double work() {
int max_ = a[1];
for(int i = 2;i <= n; ++i) {
max_ = max(a[i],max_);
}
return (double)max_;
}
int main()
{
int m,b;
scanf("%d",&n);
int tol = 0;
int max_key;
for(int i = 1 ;i <= n; ++i) scanf("%d",&a[i]),tol+=a[i];
scanf("%d",&m);
bool fg = true;
for(int i = 0;i < m; ++i) {
scanf("%d",&b);
if(!a[b]) {
fg = false;
continue;
}
double k = (double)work();
double k1 = 1.0*k/tol;
double k2 = 1.0*a[b]/tol;
if(abs(k1 - k2) > 0.2) {
fg = false;
}
tol --;
a[b] --;
}
if(fg)
puts("PASS");
else
puts("BUG");
return 0;
}
L: 馋嘴会长逛小吃街
众所周知,会长特别喜欢吃路边小吃,于是会长趁着圣诞夜晚上出完题就骑着小黄车溜到学校外面小吃街去解馋去了,小吃街是一条笔直的大街,我们可以把它抽象成是一条坐标轴,每个小吃摊都位于坐标轴上整数点的位置,而会长可以在坐标轴上的任何一个位置下车开吃,会长虽然爱吃但也很在意自己的身材,所以他只会吃k个小吃摊就回去,于是会长想知道如果自己就停一次车,然后步行去之前想吃的那些小吃摊,最后回到停车的位置,那么最短的步行路程是多少。
输入
输入的第一行为一个整数t(1<=t<=100),表示测试样例的组数。
接下来输入t组样例,每组输入占两行,第一行输入两个整数n和k(1<=n<=20,1<=k<=n),n表示想要去吃的小吃摊的位置,k表示会长最多能吃的小吃摊个数;
第二行输入n个整数,表示计划要去的那些小吃摊的位置,位置范围为[0,99]。保证没有多个小吃摊在同一个位置。
输出
对于每组输入,输出最短的步行路程。
样例输入
2
4 2
24 13 89 37
6 3
7 30 41 14 39 42
样例输出
22
6
解题思路:我们先对小吃摊的位置排序,然后从左往右每次去k个连续的小吃摊,然后扫过去找到最小的路程就OK了,时间复杂度\(O(N)\);
Code:
#include<bits/stdc++.h>
using namespace std;
int a[30];
int main()
{
int t;
int n,k;
scanf("%d",&t);
while(t--) {
scanf("%d%d",&n,&k);
for(int i = 1;i <= n; ++i) {
scanf("%d",&a[i]);
}
sort(a+1,a+n+1);
int ans = 0x3f3f3f3f;
for(int i = 1;i <= n - k + 1; ++i) {
ans = min(a[i + k - 1] - a[i], ans);
}
printf("%d\n",ans*2);
}
return 0;
}
总结
这次比赛前期状态还是可以,到了中后期思维、写代码速度还有写代码的仔细程度都有明显的下降,特别是D题,思路蛮简单,就是不仔细,写的代码的细节还是没处理好,J题(签到题)也WA了一发,得多加训练了。还有概率论和博弈论这俩东西得找个时间补补,感觉最近得比赛都在考这个,几乎每考必死。其他的题目,有时间我看看能不能补补==


 浙公网安备 33010602011771号
浙公网安备 33010602011771号