牛客编程巅峰赛S2第6场 - 钻石&王者
牛客巅峰赛钻石&王者场
前言
自从我一场从青铜打上钻石以后,我好像就打不了黄金场的哭唧唧(/(ㄒoㄒ)/~~),钻石王者场真呆不下去了
被各路神仙吊打
String II

解题思路:
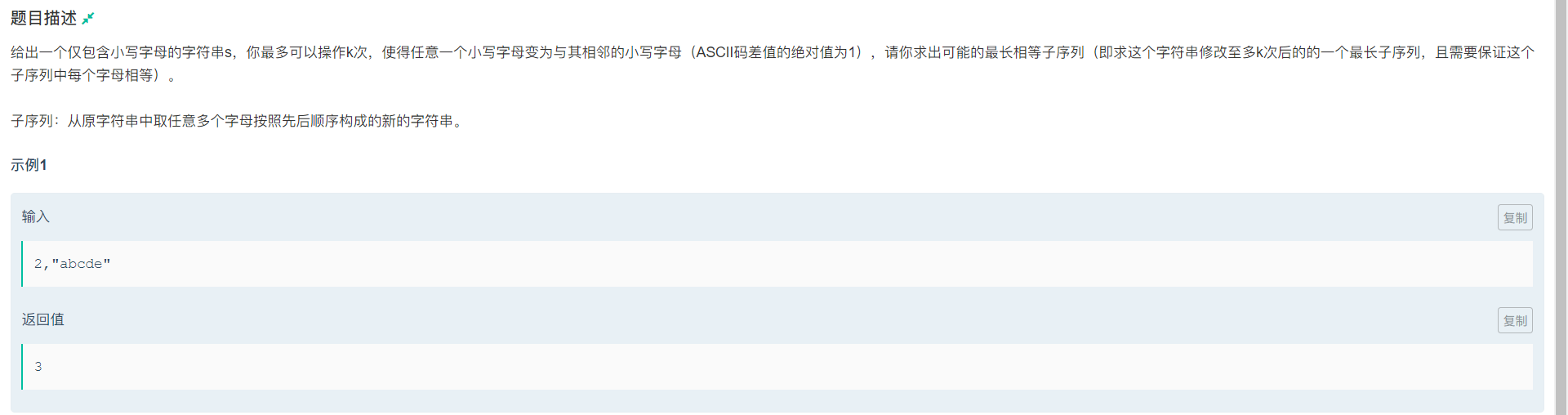
签到题,比较简单,我的思路是 差分+枚举,我们看数据只有大概1e3,那这铁定可以暴力枚举出来啊
我们枚举原串中每个位置的字母为新串的字母,然后对该字母进行差分(注意正负),然后排序后贪心选
最大的可能,时间复杂度大概是\(O(n^2logn)\),直接来看代码叭,代码好懂(⊙﹏⊙)
Code:
int string2(int k, string s) {
int pre[10005];//我们的差分数组
int ans = 1;//最少的可能就是字串只有一个
for(int i = 0;i < s.size(); ++i) {
int temp = 0;
for(int j = 0;j < s.size(); ++j) {//对第i个字符进行差分操作
pre[j] = abs(s[j]-s[i]);
}
sort(pre,pre+s.size());//对差分的结果排序,我们不在乎字母的位置
int tk = k;
int loc = 0;
for(;loc < s.size(); ++loc)//判断以第i个字母为字串的长度
if(tk - pre[loc] >= 0) {
tk -= pre[loc];
temp++;
}
else
break;
ans = max(ans,temp);//选取最大的
}
return ans;
}
其实这里我们可以优化的,因为字母的个数也就26个,我们不需要把远串所有字母全部枚举,我们只需要枚举
原串存在的不同的字母就行,这个时候的时间复杂度大概为\(26nlog(n)\)
Bang! Bang!
解题思路:
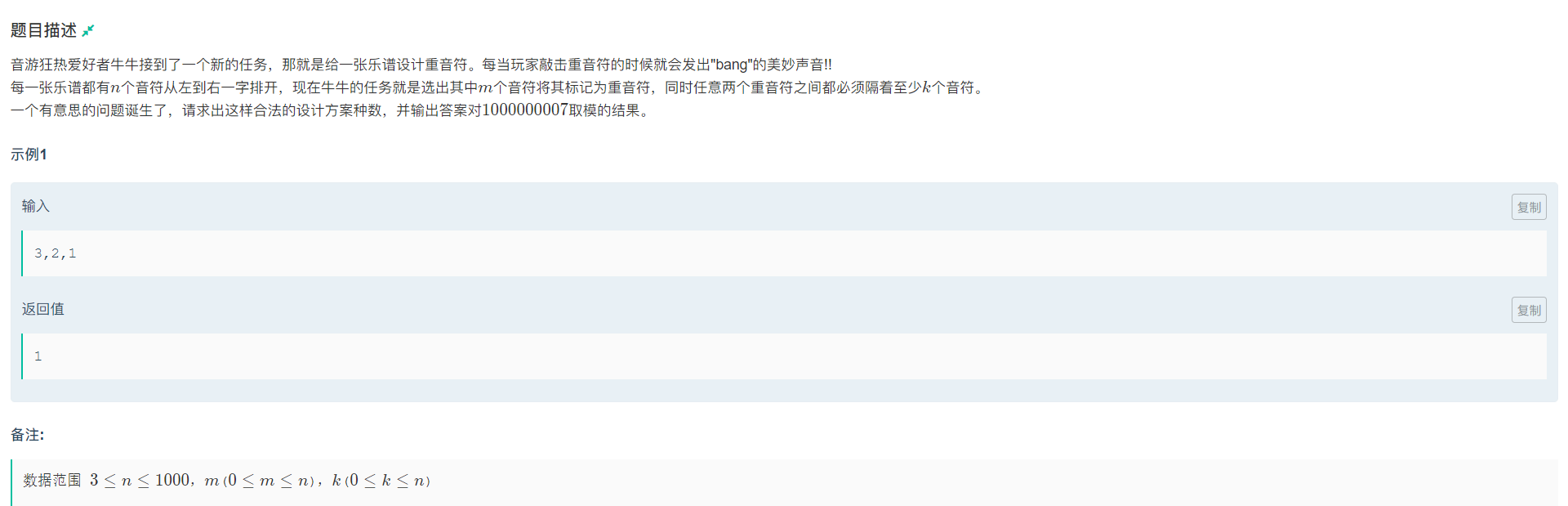
在n个音符中选取m个音符标记为重音符,重音符之间相隔至少k个音符,emmm是不是很像高中的排列组合
这题可以用排列组合的隔板法切出来,但是我不会QAQ,给个组合数学做出来的大佬的题解:传送门
言归正传,我理解的是动态规划做这题,dp[i][j]表示的是第i个重音符放在第j个位置的方案数
那么很显然结果就是ans = \(\sum_{i=1}^n dp[m][i]\),状态的初始话,我们让dp[1][i]=1,表示的是第一个重音符放的位置有n种
dp[0][0]=1表示的不放重音符,也没有音符放,也算是一种情况,我们会发现这样想后会发现dp[i][j] = dp[i-1][1]+dp[i-1][2]+……dp[i-1][j-k-1]
这样的话,我们的代码就是\(O(n^3)\)的复杂度,但是经过我们仔细的看题解分析后,我们会发现dp[i][j-1] = dp[i-1][1]+dp[i-1][2]+……dp[i-1][j-k-2]
那这样的话,我们其实就可以把状态方程改为:
Code:
const int mod = 1e9+7;
long long solve_bangbang(int n, int m, int k) {
// write code here
const int N = 1005;
int dp[N][N];
if(m == 0)//特判一下如果重音符数为0的时候,只有一种方式->就是不变
return 1;
dp[0][0] = 1;
for(int i = 1;i <= n; ++i) {//初始化
dp[1][i] = 1;
}
for(int i = 2;i <= m; ++i) {
for(int j = k + 2;j <= n; ++j) {
dp[i][j] = (dp[i][j-1]+dp[i-1][j-k-1]) % mod;//状态转移方程
}
}
int ans = 0;
for(int i = 0;i <= n; ++i) {
ans = (ans + dp[m][i]) % mod;//最后把所有的情况加起来
}
return ans % mod;
}
天花板
解题思路:
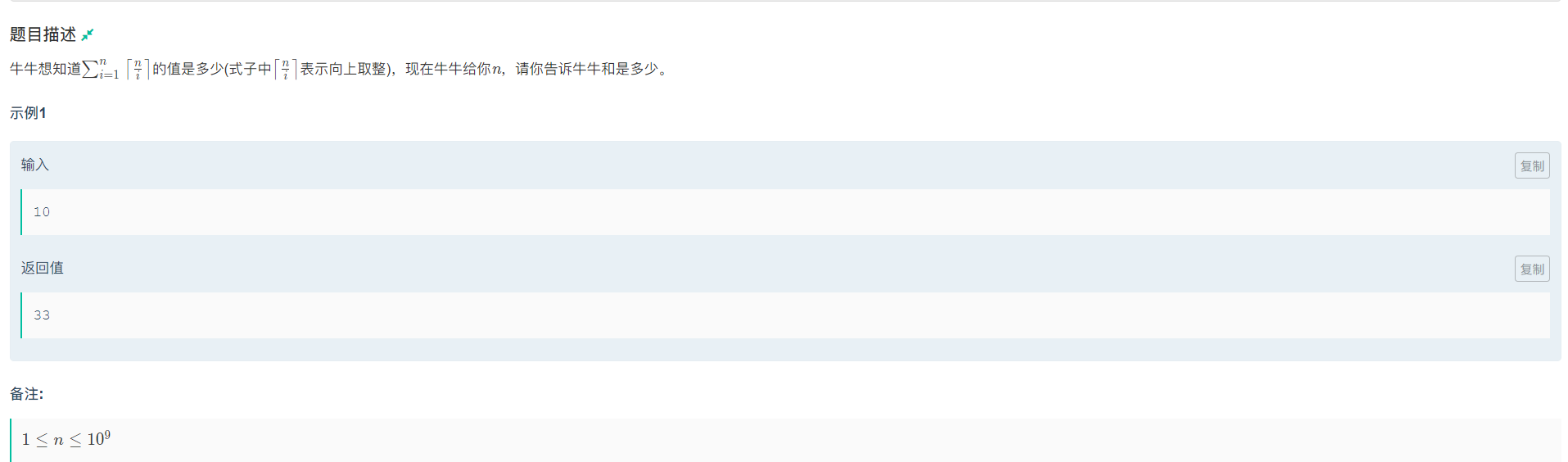
这题是整除分块的板子题……,然鹅我并没有学,我在这题上耗了半小时,我还傻乎乎的以为是推一个公式,手动模拟
了一下前十的数据,好像发现了什么规律,但是好像什么都没发现,然后滚去学了一手整数分块,原理蛮简单的,
\(\lceil\)\(\frac{N}{i}\)\(\rceil\)的个数不会超过\(2\sqrt{N}\)个,这里就要引用一个推导的结论了,\(\sum_{i=1}^n \lceil\)\(\frac{N}{i}\)\(\rceil = \sum_{l=1}^n (r-l+1)\lceil\)\(\frac{N}{l}\)\(\rceil\),
但是其中的r是一直在变化\(r=\lceil\)\(\frac{N}{\lceil\frac{N}{l}\rceil}\)\(\rceil\),然后把l从1遍历到n就行,时间复杂度为\(O(n)\)
关于这个结论的推导和其他推论的运用传送门一,传送门二
Code:
long long Sum(int n) {
// write code here
long long ans = 0;
long long l,r;
l = 1;
for(;l<=n;l = r + 1) {
if((n-1)/l)
r =(n-1)/((n-1)/l);
else
r = n;
r = min(r,(long long)n);
ans += (r - l + 1) * (((n-1)/l)+1);
}
return ans;
}
ps:今天写了好多latex……还有点不习惯。
/*
┏┛ ┻━━━━━┛ ┻┓
┃ ┃
┃ ━ ┃
┃ ┳┛ ┗┳ ┃
┃ ┃
┃ ┻ ┃
┃ ┃
┗━┓ ┏━━━┛
┃ ┃ 神兽保佑
┃ ┃ 代码无BUG!
┃ ┗━━━━━━━━━┓
┃ ┣┓
┃ ┏┛
┗━┓ ┓ ┏━━━┳ ┓ ┏━┛
┃ ┫ ┫ ┃ ┫ ┫
┗━┻━┛ ┗━┻━┛
*/



