2020 年百度之星程序设计大赛 - 初赛二
Poker
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 98 Accepted Submission(s): 39
传送门
Problem Description
小沃沃在玩一个有趣的游戏。
初始他有 n 块钱,每一轮他需要投入至少 m 块钱,系统会拿走其中 p% 的钱,并把剩下的钱还给他。
请问在最优情况下,小沃沃最多可以玩多少轮?
假设当前一轮小沃沃投入了 x 块钱,那么他可以收回 ⌊x×(1−p%)⌋ 块钱,其中 ⌊a⌋ 表示 a 取下整。
小沃沃每一轮投入的钱不能超过他现在拥有的钱。
每一轮投入的钱必须为整数。
初始他有 n 块钱,每一轮他需要投入至少 m 块钱,系统会拿走其中 p% 的钱,并把剩下的钱还给他。
请问在最优情况下,小沃沃最多可以玩多少轮?
假设当前一轮小沃沃投入了 x 块钱,那么他可以收回 ⌊x×(1−p%)⌋ 块钱,其中 ⌊a⌋ 表示 a 取下整。
小沃沃每一轮投入的钱不能超过他现在拥有的钱。
每一轮投入的钱必须为整数。
Input
第一行一个正整数 test(1≤test≤100000) 表示数据组数。
对于每组数据,一行三个整数 n,m,p(1≤n≤100000,1≤m≤1000,1≤p≤100)。
对于每组数据,一行三个整数 n,m,p(1≤n≤100000,1≤m≤1000,1≤p≤100)。
Output
对每组数据输出一行一个整数表示答案。
Sample Input
2
10 2 50
10 2 100
Sample Output
9 5
解题思路:签到题,每次至少投入m快钱,每次系统拿掉p%也就是说每次会减少m*p%的钱,用一个循环,每次模拟,当剩下的钱不够m的时候退出就行
AC代码:
#include<cstdio> int main(void) { int t,n,m,p; scanf("%d",&t); while(t--) { scanf("%d%d%d",&n,&m,&p); int sum=0; while(n>=m)//判断条件 { n-=(m*p/100.0);//每次减少的钱 sum++; } printf("%d\n",sum); } return 0; }
Distance
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 65 Accepted Submission(s): 21
传送门
Problem Description
小沃沃所在的世界是一个二维平面。他有 n 个朋友,第 i 个朋友距离他的距离为 a[i],小沃沃并不知道这些朋友具体在什么点上。
请问在最优情况下,小沃沃的朋友两两之间的欧几里得距离的和的最小值是几?
假设小沃沃的位置为 P0=(x0,y0),第 i 个朋友的位置为 Pi=(xi,yi),对于所有的 i,需要满足 dist(P0,Pi)=a[i],并且∑n−1i=1∑nj=i+1dist(Pi,Pj) 最小,其中 dist(X,Y) 为连接点 X 和点 Y 的线段的长度。xi,yi 都可以是任意实数。
请问在最优情况下,小沃沃的朋友两两之间的欧几里得距离的和的最小值是几?
假设小沃沃的位置为 P0=(x0,y0),第 i 个朋友的位置为 Pi=(xi,yi),对于所有的 i,需要满足 dist(P0,Pi)=a[i],并且∑n−1i=1∑nj=i+1dist(Pi,Pj) 最小,其中 dist(X,Y) 为连接点 X 和点 Y 的线段的长度。xi,yi 都可以是任意实数。
Input
第一行一个正整数 test(1≤test≤10) 表示数据组数。
对于每组数据,第一行一个正整数 n(1≤n≤100000)。
接下来一行 n 个整数,第 i 个整数 a[i](1≤a[i]≤1000000000) 表示第 i 个朋友和小沃沃的距离。
对于每组数据,第一行一个正整数 n(1≤n≤100000)。
接下来一行 n 个整数,第 i 个整数 a[i](1≤a[i]≤1000000000) 表示第 i 个朋友和小沃沃的距离。
Output
对每组数据输出一行一个数,表示 ∑n−1i=1∑nj=i+1dist(Pi,Pj) 的最小值。答案需要四舍五入到整数。
Sample Input
2
2
3 5
5
1 2 3 4 5
Sample Output
2
20
解题思路:不要被题目的表面迷惑了,什么xi,yi对题目没有任何影响,我们只知道小沃沃的朋友距离小沃沃的长度,什么时候他的朋友们的相互距离之和最小呢,我们都知道直线有最短距离
那么他的朋友就是站成一条直线的。我们会想到用一个两层循环去做,有些人就存在侥幸心理,莽一发O(n^2)直接交上去,然后秒T,没错就是我,,。
T掉之后,我们就会想优化,其实很容易发现当朋友们连成一条直线的时候,对朋友们的距离进行排序,就能得到有序的数组,然后我们发现在计算的时候会有重复的部分,然后我们减去重复的部分就好了啊。
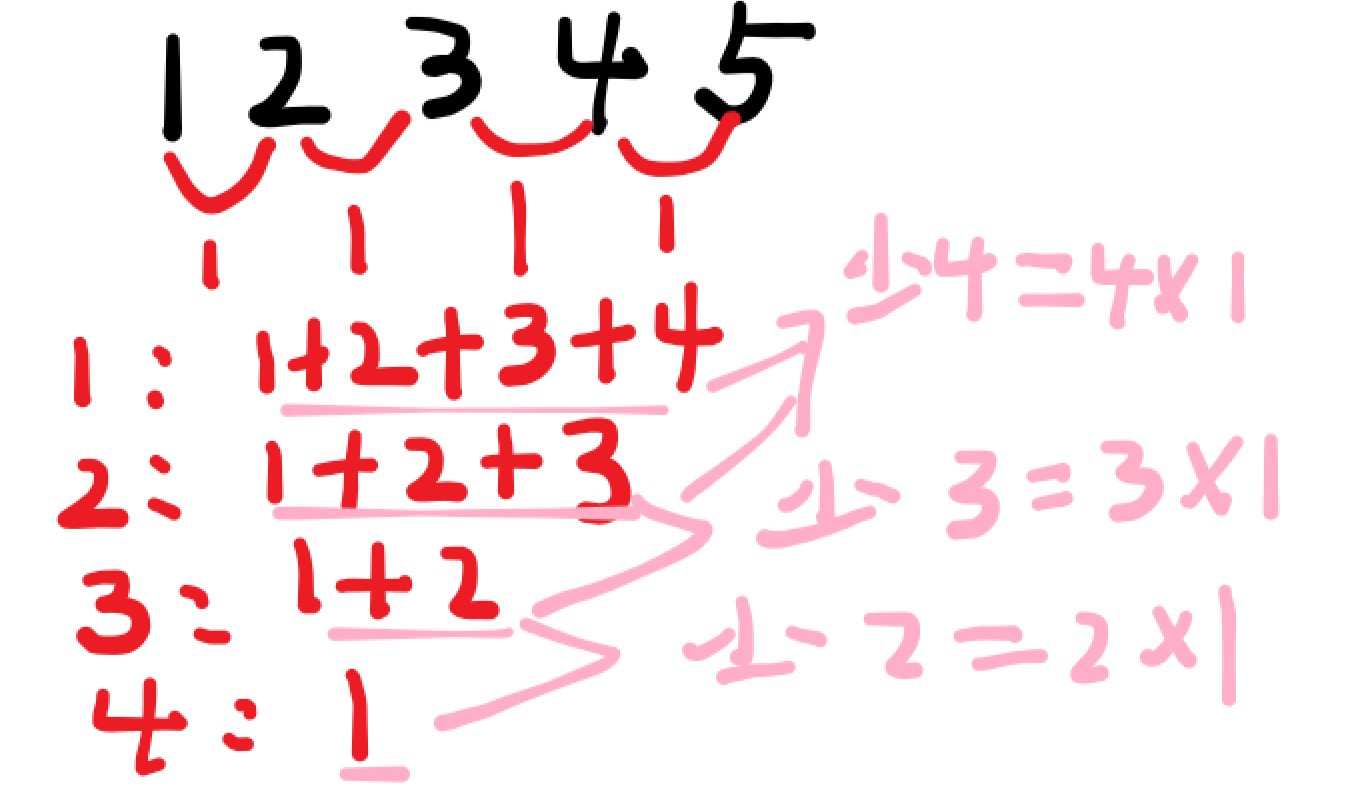
设K为第一个到其他的总和,那么k0=10,然后每次减去(n-i)*b[i],不断让k更新。
AC代码:
#include<cstdio> #include<algorithm> using namespace std; #define maxn 100005 #define ll long long bool cmp(ll a,ll b) { return a<b; } ll a[maxn],b[maxn]; int main(void) { ll t,n; scanf("%lld",&t); while(t--) { scanf("%lld",&n); ll sum=0; for(ll i=0;i<n;++i) { scanf("%lld",&a[i]); } sort(a,a+n,cmp); ll k=0;//这个k表示的是第一个朋友到其他朋友的距离总和 for(ll i=1;i<n;++i) { b[i]=a[i]-a[i-1];//求相邻朋友的距离 k+=(n-i)*b[i]; } for(ll i=1;i<n;++i) { sum+=k;//每次加上每个朋友到其他朋友的距离(未被添加距离的朋友) k-=(n-i)*b[i];//更新k的值 } printf("%lld\n",sum); } }
本文作者:MangataTS
本文链接:https://www.cnblogs.com/Mangata/p/13377959.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。







【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步