洛谷 P2181 对角线

P2181 对角线

传送门

题目描述

对于一个 n 个顶点的凸多边形，它的任何三条对角线都不会交于一点。请求出图形中对角线交点的个数。

例如，6 边形：

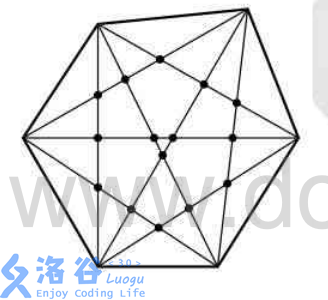
输入格式

输入只有一行一个整数 n，代表边数。

输出格式

输出一行一个整数代表答案。

输入输出样例

输入 #1

3

输出 #1

0

输入 #2

6

输出 #2

15

说明/提示

数据规模与约定

对于 50% 的数据， 保证 3≤n≤100。
对于 100% 的数据，保证 3≤n≤105。

解题思路：开始我以为是个纯几何问题，然后，我开始找规律，从3开始然后并没看出规律(可能是我太菜了)，
在思索一番之后我还是看了下大佬的思路，看完后恍然大悟，我们知道交点是由两根线组成的，也就是说需要四个顶点为这两根线的组成做贡献
想通了这个，我们就不难发现，我们求的交点个数相当于是求在这个多边形的交线中求出两个不同交线的个数，也就是在多边形的顶点中选取四个不同顶点的数目(还是很好理解的吧)
到了这里我们发现这个问题是一个组合数学的问题结果就是Cn4,就是在n个元素中选取四个的情况总数。
然后你以为就完了嘛，看一眼数据，1e5直接爆long long，但是我们不用写高精度，这里有个比较巧妙的方法：
n*(n-1)*(n-2)*(n-3)/24==n*(n-1)/2*(n-2)/3*(n-3)/4
先来说说为什么这么做能保证结果是整数
n和n-1是两个相邻的数，2的倍数一定是个偶数，而n和n-1必定有一个数为偶数（相邻的两个数必定有一个为2的倍数）
相邻的三个数必定有一个为3的倍数，那么4也就同理(其实这是初中的知识)

那么可得如下代码：

• #include<bits/stdc++.h>
  using namespace std;
  #define ll unsigned long long
  #pragma-GCC-optimize("-Ofast");
  int main(void)
  {
      ios::sync_with_stdio(false);
      ll n;
      cin>>n;
      cout<<n*(n-1)/2*(n-2)/3*(n-3)/4<<endl;
  }

  附上大佬的题解：传送门