luogu 2698 [USACO12MAR]花盆Flowerpot

 

题目描述

Farmer John has been having trouble making his plants grow, and needs your help to water them properly. You are given the locations of N raindrops (1 <= N <= 100,000) in the 2D plane, where y represents vertical height of the drop, and x represents its location over a 1D number line:

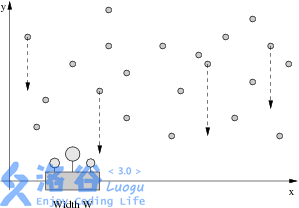
Each drop falls downward (towards the x axis) at a rate of 1 unit per second. You would like to place Farmer John's flowerpot of width W somewhere along the x axis so that the difference in time between the first raindrop to hit the flowerpot and the last raindrop to hit the flowerpot is at least some amount D (so that the flowers in the pot receive plenty of water). A drop of water that lands just on the edge of the flowerpot counts as hitting the flowerpot.

Given the value of D and the locations of the N raindrops, please compute the minimum possible value of W.

老板需要你帮忙浇花。给出N滴水的坐标，y表示水滴的高度，x表示它下落到x轴的位置。

每滴水以每秒1个单位长度的速度下落。你需要把花盆放在x轴上的某个位置，使得从被花盆接着的第1滴水开始，到被花盆接着的最后1滴水结束，之间的时间差至少为D。

我们认为，只要水滴落到x轴上，与花盆的边沿对齐，就认为被接住。给出N滴水的坐标和D的大小，请算出最小的花盆的宽度W。

输入格式

第一行2个整数 N 和 D。

第2.. N+1行每行2个整数，表示水滴的坐标(x,y)。

输出格式

仅一行1个整数，表示最小的花盆的宽度。如果无法构造出足够宽的花盆，使得在D单位的时间接住满足要求的水滴，则输出-1。

输入输出样例

输入 #1 
4 5
6 3
2 4
4 10
12 15
输出 #1 
2

说明/提示

【样例解释】

有4滴水， (6,3), (2,4), (4,10), (12,15).水滴必须用至少5秒时间落入花盆。花盆的宽度为2是必须且足够的。把花盆放在x=4..6的位置，它可以接到1和3水滴, 之间的时间差为10-3 = 7满足条件。

【数据范围】

40%的数据：1 ≤ N ≤ 1000，1 ≤ D ≤ 2000；

100%的数据：1 ≤ N ≤ 100000，1 ≤ D ≤ 1000000，0≤x,y≤10^6。

 

分析

看数据范围，结合题意，求高度差大于等于d的最短距离

单调队列

枚举结束的点

用两个队列分别维护最大值与最小值

求差更新答案便好

代码

 1 /**************************
 2 User£ºMandy.H.Y
 3 Language:c++
 4 Problem£º 
 5 **************************/
 6 
 7 #include<bits/stdc++.h>
 8 
 9 using namespace std;
10 
11 const int maxn = 1e5 + 5;
12 const int maxd = 1e6 + 5;
13 
14 int n,d;
15 int l1,r1,q1[maxn];
16 int l2,r2,q2[maxn];
17 
18 struct Node{
19     int x,y;
20 }node[maxn];
21 
22 template<class T>inline void read(T &x){
23     x = 0;bool flag = 0;char ch = getchar();
24     while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
25     while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
26     if(flag) x = -x;
27 }
28 
29 template<class T>void putch(const T x){
30     if(x > 9) putch(x / 10);
31     putchar(x % 10 | 48);
32 }
33 
34 template<class T>void put(const T x){
35     if(x < 0) putchar('-'),putch(-x);
36     else putch(x);
37 }
38 
39 void file(){
40     freopen("1232.in","r",stdin);
41     freopen("1232.out","w",stdout);
42 }
43 
44 bool cmp(const Node &a,const Node &b){
45     return a.x < b.x;
46 }
47 
48 void readdata(){
49     read(n);read(d);
50     for(int i = 1;i <= n; ++ i){
51         read(node[i].x);
52         read(node[i].y);
53     } 
54     sort(node + 1,node + n + 1,cmp);
55 }
56 
57 void work(){
58     int ans = node[n].x + 100;
59     for(int i = 1;i <= n; ++ i){
60         while(l1 < r1 && node[i].x-node[q1[l1]].x>=ans) l1++;
61         while(l2 < r2 && node[i].x-node[q2[l2]].x>=ans) l2++;
62         if(l1 < r1 && abs(node[i].y-node[q1[l1]].y) >= d) ans = min(ans,node[i].x-node[q1[l1]].x);
63         if(l2 < r2 && abs(node[i].y-node[q2[l2]].y) >= d) ans = min(ans,node[i].x-node[q2[l2]].x);
64         while(l1 < r1 && node[i].y < node[q1[r1-1]].y) r1--;
65         while(l2 < r2 && node[i].y < node[q2[r2-1]].y) r2--;
66         q1[r1++] = i;
67         q2[r2++] = i;
68     }
69     if(ans > node[n].x - node[1].x) puts("-1");
70     else put(ans);
71 }
72 
73 int main(){
74 //    file();
75     readdata();
76     work();
77     return 0;
78 }
View Code

 

posted @ 2019-09-09 21:58  Mandy_H_Y  阅读(149)  评论(0)  编辑  收藏  举报